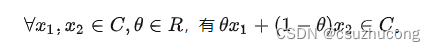
凸优化、共轭、对偶、对偶梯度下降、原始对偶

本文部分内容来自。

csuzhucong

2660人浏览 · 2023-06-30 10:07:50

csuzhucong · 2023-06-30 10:07:50 发布

前些天发现了一个巨牛的人工智能学习网站，通俗易懂，风趣幽默，忍不住分享一下给大家：点击跳转

一，仿射集、仿射包

1，仿射集(affine set)

2，仿射组合(affine combination)

四，极点、回收方向、回收锥、极向量、极方向

5，Chambolle-Pock、C++实现

6，随机PDHG算法（SPDHG）

7，python odl源码

本文部分内容来自网友文章和网友文章

后来发现网友的内容似乎来自北大教材链接

一，仿射集、仿射包

1，仿射集(affine set)

满足如下条件的集合叫仿射集：

直线是仿射集，线段不是

2，仿射组合(affine combination)

3，仿射包(affine hull)

对任意集合 A，增加最少的元素使 A 变为仿射集 B ，则仿射集 B 是 A 的仿射包，即 B 是包含 A的最小仿射集。

线段的仿射包是包含这条线段的直线，平面多边形（三角形，正方形等）的仿射包是包含此多边形的整个平面。

仿射集的仿射包是它自身。

二，凸集、凸包

1，凸集

仿射集都是凸集，凸集不一定是仿射集，如线段、凸多边形。

2，凸组合

3，凸包(convex hull)

对任意集合 A，增加最少的元素使A 变为凸集B ，则凸集B 是 A 的凸包，即 B 是包含 A 的最小凸集。

凸集的凸包是其本身。

三，凸锥、锥包

1，凸锥(convex cone)

锥其实就是若干（有限或无限）条从原点出发的射线组成的。

设函数f是射线到角度的映射，角度范围是[0,2π)，那么：

一个锥是凸锥等价于这个锥作为定义域时f的值域是凸集（即凸的线段）

除了单射线和平面点全集之外，其他凸锥的边界就是2条射线，所构成的夹角一定在(0,π]区间内。

2，锥组合

3，锥包(cone hull)

对任意集合 A，增加最少的元素使 A 变为凸锥 B ，则凸锥 B 是 A 的锥包，即 B 是包含 A 的最小凸锥。

四，极点、回收方向、回收锥、极向量、极方向

1，极点

凸集中不能表示成两个不同点的凸组合的点，叫做极点。

2，回收方向、回收锥

非空凸集 $S$ 的所有回收方向构成的凸锥（包括零向量），称为 $S$ 的回收锥

如凸集{y>=x^2}的回收锥是{x=0, y>=0}, 凸集{y>=e^x}的回收锥是{x<=0,y>=0}

如有限凸集的回收锥一定是{x=0，y=0}，即只有零向量这一个回收方向。

3，极向量、极方向

凸锥中不能表示成其他向量的锥组合的向量，称为极向量。

凸集的回收锥的极向量，称为该凸集的极方向。

如凸锥{x<=0,y>=0}的极向量的集合是{x=0，y>=0}∪{x<=0,y=0}，凸集{y>=e^x}的极方向的集合也是它。

五，凸函数

1，凸函数

一般有3种说法：

（1）f1是凸函数，f2是凹函数

（2）f1是凹函数，f2是凸函数

（3）f1是下凸函数，f2是上凸函数，都是凸函数

都是一样的意思，仅仅叫法不同而已，不用太在意。

用（1）说法来定义凸函数：

我个人喜欢用（3）说法，因为他不参与（1）和（2）的争斗。

上凸函数中，点集{y<f2(x)}是凸集，下凸函数中，点集{y>f1(x)}是凸集。

2，一阶条件

3，二阶条件

如果是多元函数，它的二阶导数是Hessian矩阵。

4，示性函数

凸集的示性函数为凸函数。

六，共轭函数

1，共轭函数

sup是上确界，dom是定义域。

2，示例

3，共轭函数的性质

（1）函数的共轭函数是凸函数

（2）凸函数f的共轭函数的共轭函数是f本身

以一元可微凸函数为例，推导如下：

所以共轭函数的共轭函数的它本身。

其中，式（1）也叫勒让德变换。

我们说凸函数f的共轭函数的共轭函数是f本身，其实也就是说勒让德变换是自身的逆变换。

（3）共轭函数的导数和原函数的导数互为反函数

即上面的式（2）。

（4）线性变换

$g(y)=af(y)\rightarrow g^*(y)=af^*(y/a)$

推导：

$g(y)=af(y)\\g^*(y)=sup(y^Tx-g(y))=a*sup(y^T\frac{x}{a}-f(y))=af^*(\frac{y}{a})$

七，对偶梯度下降

1，对偶问题

原始问题

对偶函数

对偶问题

2，KKT条件

对一般的原问题，KKT 条件是取到最优解的必要条件。

对原问题为凸问题， KKT 条件是取到最优解的充要条件。

3，弱对偶、强对偶

弱对偶：原问题最小值大于等于对偶问题最大值。弱对偶恒成立。

强对偶：原问题和对偶问题的最优值相等。强对偶并不恒成立。

4，SCQ条件

5，对偶问题的例子

在原问题比较简单的情况下，可以把对偶问题的具体表达式推导出来。

（1）单个函数+线性约束

D的推导：

（2）函数+函数+线性约束

P：

D：

（3）函数+复合函数

$P:min\, f(x)+g(h(x))\\ D:max_\lambda (inf_x(f(x)+\lambda h(x))-g^*(\lambda ^T))$

D的推导：

（4）函数+复合线性函数 h(x) = Ax

$P:min\, f(x)+g(Ax)\\ D:max_z (-f^*(-A^Tz)-g^*(z ^T))$

6，对偶梯度下降、对偶分解

把原问题，转化成对偶问题，并用梯度或次梯度做梯度下降的迭代算法。

（1）单个函数+线性约束

这个例子中，原问题求f(x)的最小值，和次梯度中求x其实差不多，看不出对偶的效果。

（2）函数+函数+线性约束

P：

D：

次梯度下降：

相比求f1+f2的最小值，对偶问题的次梯度是把f1和f2完全分开计算的，这就是对偶分解的优势所在。

7，对偶近端梯度下降

对偶近端梯度下降就是把有问题P转化成对偶问题D，再用近端梯度下降。

示例：

其中f和g 是凸函数。

如果对P用近端梯度下降，则需要求G(x)=g(Ax)这个复合函数的近端映射函数。

而如果转化成D，那么就只需要求g*的近端映射函数即可。

根据近端梯度下降公式变换得到：对偶近端梯度下降公式：

根据前面的“共轭函数的次梯度计算”，这个公式可以表示成2步：

即，原问题P化为2个小问题，一是只含f的最优值计算，二是g*的近端映射函数。

再根据广义Moreau 分解可以把g*的近端映射函数化成g的近端映射函数，从而把迭代公式表示成3步：

八，一阶原始对偶

本章示例：

P：min f(x) + g(Ax)，其中f和g 是凸函数。

1，部分拉格朗日函数

拉格朗日函数： $L(x,y)=f(x)+\lambda ^TAx+ g(y)-\lambda ^Ty$

部分拉格朗日函数： $h(x,z)=f(x)-g^*(z)+z^TAx$

2，一阶原始对偶

由于h既含有f的原函数，又含有g的共轭函数，所以我们把关于h的优化问题称为一阶原始对偶。

3，对偶混合梯度下降 (PDHG)

KKT条件：

本例中，KKT条件化简成：

∂L/∂x = 0 （1）

∂L/∂y = 0 （2）

y=Ax （3）

λ>=0 （4）

其中（1）可以化成： $0\in\delta f(x)+A^T\lambda$ （5）

（2）可以化成 $0 \in \delta g(y)-\lambda$ 即 $\lambda \in \delta g(y)$ 即 $y\in \delta g^*(\lambda)$ （6）

联合（3）（6）消掉y得到：

$Ax\in \delta g^*(\lambda)$ （7）

而（5）（7）联合起来，等价于寻找h的鞍点，即调整x使得h最小，调整λ使得h最大。

在近端梯度下降和对偶近端梯度下降中，优化目标的2个部分都是同一个自变量，所以不能很好的解耦。

而在一阶原始对偶h(x,z)中，x和z是完全解耦的，所以迭代过程很直观，就是交替对x和z做近端映射即可，我们称之为对偶混合梯度下降。

4，部分拉格朗日函数的近端映射

$h(x,z)=f(x)-g^*(z)+z^TAx$

以x为例，把h看做关于x的函数，h是在f的基础上，加了常量-g^*(z)，再加了线性函数z^TAx

那么根据近端映射的运算法则：

$prox_{t,h}(x)=prox_{t,f}(x-tA^Tz)$

同理， $prox_{t,h}(z)=prox_{t,g^*}(z+tA^Tx)$

这样就得到了PDHG的迭代公式：

$z_{k+1}=prox_{t_kg^*}(z_k+t_kAx_k)\\ x_{k+1}=prox_{a_kf}(x_k-a_kA^Tz_{k+1})$

这2步交替进行，不断刷新x和z的值即可。

5，Chambolle-Pock、C++实现

Chambolle-Pock和PDHG非常像，加了一个外推操作，感觉就是做了简单的加速，提高了步长。

PS：近端映射函数 $prox_{t,f}(x)$ 中的t涉及到最终是否收敛，所以取值受限于一个范围，并不是只要调整t就能加速。

Chambolle-Pock的迭代公式：

$z_{k+1}=prox_{t_kg^*}(z_k+t_kAy_k)\\ x_{k+1}=prox_{a_kf}(x_k-a_kA^Tz_{k+1})\\ y_{k+1}=x_{k+1}+\theta (x_{k+1}-x_k), \theta >0$

一般取 $\theta$ =1

下面是我实现的ChambollePock算法，没有支持每次迭代都使用不同的t和a。

vector<float> add(const vector<float>&x1, const vector<float>&x2)
{
	vector<float>ans(x1.size(), 0);
	for (int i = 0; i < x1.size(); i++)ans[i] = x1[i] + x2[i];
	return ans;
}
vector<float> multi(float t, const vector<float>&x)
{
	vector<float>ans(x.size(), 0);
	for (int i = 0; i < x.size(); i++)ans[i] = x[i];
	return ans;
}
vector<float> multi(const vector<vector<float>>&A, const vector<float>&x)
{
	vector<float>ans(x.size(), 0);
	for (int i = 0; i < x.size(); i++) {
		for (int j = 0; j < x.size(); j++)ans[i] += A[i][j] * x[j];
	}
	return ans;
}
vector<vector<float>> T(const vector<vector<float>>&A)
{
	vector<vector<float>>ans = A;
	for (int i = 0; i < A.size(); i++) {
		for (int j = 0; j < A.size(); j++) {
			ans[i][j] = A[j][i];
		}
	}
	return ans;
}
vector<float> prox_f(float t, vector<float>x)
{
	return x;  //自定义
}
vector<float> prox_g_conjugate(float t, vector<float>z)
{
	return z;//自定义
}
// solve min h(x) max h(z) , which h(x,z)=f(x)-g_conjugate(z)+z^T * A * x
void ChambollePock(vector<float> &x,vector<float>&z, const vector<vector<float>>&A,int t, int a, int learningTimes, int theta = 1) //x and z is both input and output
{
	vector<float>y = x;
	auto AT = T(A);
	for (int i = 0; i < learningTimes; i++) {
		z = prox_g_conjugate(t, add(z, multi(t, multi(A, y))));
		y = multi(-theta, x);
		x = prox_f(a, add(x, multi(-a, multi(AT, z))));
		y = add(multi(theta + 1, x), y);
	}
}

只需要根据实际情况提供2个prox函数即可调用。

6，随机PDHG算法（SPDHG）

在Chambolle-Pock的基础上，把 $\theta$ 当成一个对角矩阵，其中对角线上每个分量随机取0或者1

即x不一定各个方向都往外推，可能只是一部分方向往外推。

7，python odl源码

在stochastic_primal_dual_hybrid_gradient.py中有spdhg的接口：

def spdhg_generic(x, f, g, A, tau, sigma, niter, **kwargs):
    r"""Computes a saddle point with a stochastic PDHG.

    This means, a solution (x*, y*), y* = (y*_1, ..., y*_n) such that

    (x*, y*) in arg min_x max_y sum_i=1^n <y_i, A_i> - f*[i](y_i) + g(x)

    where g : X -> IR_infty and f[i] : Y[i] -> IR_infty are convex, l.s.c. and
    proper functionals. For this algorithm, they all may be non-smooth and no
    strong convexity is assumed.

    Parameters
    ----------
    x : primal variable
        This variable is both input and output of the method.
    f : functions
        Functionals Y[i] -> IR_infty that all have a convex conjugate with a
        proximal operator, i.e.
        f[i].convex_conj.proximal(sigma[i]) : Y[i] -> Y[i].
    g : function
        Functional X -> IR_infty that has a proximal operator, i.e.
        g.proximal(tau) : X -> X.
    A : functions
        Operators A[i] : X -> Y[i] that possess adjoints: A[i].adjoint
    tau : scalar / vector / matrix
        Step size for primal variable. Note that the proximal operator of g
        has to be well-defined for this input.
    sigma : scalar
        Scalar / vector / matrix used as step size for dual variable. Note that
        the proximal operator related to f (see above) has to be well-defined
        for this input.
    niter : int
        Number of iterations

    Other Parameters
    ----------------
    y : dual variable, optional
        Dual variable is part of a product space. By default equals 0.
    z : variable, optional
        Adjoint of dual variable, z = A^* y. By default equals 0 if y = 0.
    mu_g : scalar
        Strong convexity constant of g.
    theta : scalar
        Global extrapolation factor.
    extra: list
        List of local extrapolation paramters for every index i. By default
        extra_i = 1.
    fun_select : function
        Function that selects blocks at every iteration IN -> {1,...,n}. By
        default this is serial uniform sampling, fun_select(k) selects an index
        i \in {1,...,n} with probability 1/n.
    callback : callable, optional
        Function called with the current iterate after each iteration.

    References
    ----------
    [CERS2017] A. Chambolle, M. J. Ehrhardt, P. Richtarik and C.-B. Schoenlieb,
    *Stochastic Primal-Dual Hybrid Gradient Algorithm with Arbitrary Sampling
    and Imaging Applications*. ArXiv: http://arxiv.org/abs/1706.04957 (2017).

    [E+2017] M. J. Ehrhardt, P. J. Markiewicz, P. Richtarik, J. Schott,
    A. Chambolle and C.-B. Schoenlieb, *Faster PET reconstruction with a
    stochastic primal-dual hybrid gradient method*. Wavelets and Sparsity XVII,
    58 (2017) http://doi.org/10.1117/12.2272946.
    """
    # Callback object
    callback = kwargs.pop('callback', None)
    if callback is not None and not callable(callback):
        raise TypeError('`callback` {} is not callable'
                        ''.format(callback))

    # Dual variable
    y = kwargs.pop('y', None)
    if y is None:
        y = A.range.zero()

    # Adjoint of dual variable
    z = kwargs.pop('z', None)
    if z is None:
        if y.norm() == 0:
            z = A.domain.zero()
        else:
            z = A.adjoint(y)

    # Strong convexity of g
    mu_g = kwargs.pop('mu_g', None)
    if mu_g is None:
        update_proximal_primal = False
    else:
        update_proximal_primal = True

    # Global extrapolation factor theta
    theta = kwargs.pop('theta', 1)

    # Second extrapolation factor
    extra = kwargs.pop('extra', None)
    if extra is None:
        extra = [1] * len(sigma)

    # Selection function
    fun_select = kwargs.pop('fun_select', None)
    if fun_select is None:
        def fun_select(x):
            return [int(np.random.choice(len(A), 1, p=1 / len(A)))]

    # Initialize variables
    z_relax = z.copy()
    dz = A.domain.element()
    y_old = A.range.element()

    # Save proximal operators
    proximal_dual_sigma = [fi.convex_conj.proximal(si)
                           for fi, si in zip(f, sigma)]
    proximal_primal_tau = g.proximal(tau)

    # run the iterations
    for k in range(niter):

        # select block
        selected = fun_select(k)

        # update primal variable
        # tmp = x - tau * z_relax; z_relax used as tmp variable
        z_relax.lincomb(1, x, -tau, z_relax)
        # x = prox(tmp)
        proximal_primal_tau(z_relax, out=x)

        # update extrapolation parameter theta
        if update_proximal_primal:
            theta = float(1 / np.sqrt(1 + 2 * mu_g * tau))

        # update dual variable and z, z_relax
        z_relax.assign(z)
        for i in selected:

            # save old yi
            y_old[i].assign(y[i])

            # tmp = Ai(x)
            A[i](x, out=y[i])

            # tmp = y_old + sigma_i * Ai(x)
            y[i].lincomb(1, y_old[i], sigma[i], y[i])

            # y[i]= prox(tmp)
            proximal_dual_sigma[i](y[i], out=y[i])

            # update adjoint of dual variable
            y_old[i].lincomb(-1, y_old[i], 1, y[i])
            A[i].adjoint(y_old[i], out=dz)
            z += dz

            # compute extrapolation
            z_relax.lincomb(1, z_relax, 1 + theta * extra[i], dz)

        # update the step sizes tau and sigma for acceleration
        if update_proximal_primal:
            for i in range(len(sigma)):
                sigma[i] /= theta
            tau *= theta

            proximal_dual_sigma = [fi.convex_conj.proximal(si)
                                   for fi, si in zip(f, sigma)]
            proximal_primal_tau = g.proximal(tau)

        if callback is not None:
            callback([x, y])