导言

符号多项式处理，是表处理的典型范例。而这章就是主要就本经典案例进行讨论。

一元多项式介绍

数学上，一个一元多项式$p_n(x)$可以按照升幂写成

$$p_n(x)=p_0+p_1x+p_2x^2+...+p_nx^n$$
它由n+1个系数唯一确定。因此在计算机里面，它可以由一个线性表P来表示：
$$P=(p_0,p_1,p_2,...,p_n)$$
每一项的指数i隐含在其系数 $p_i$的序号里。
假设 $Q_m(x)$是一元 $m$次多项式，同样可用线性表Q来表示：
$$Q=(q_0,q_1,q_2,...,q_m)$$
为了不失去一般性，我们假设 $m<n$,则两个多项式相加的结果 $R_nx=P_n(x)+Q_mx$ 可用线性表R来表示: $$R=(p_0+q_0,p_1+q_1,p_2+q_2,...,p_m+q_m,p_{m+1},...,p_n)$$

显然，我们可以对$P、Q和R$采用顺序存储机构，使得多项式相加的算法定义十分简洁。至此，一元多项式的表示及相加问题似乎已经解决了。然而，在通常的应用中，多项式的次数可能很高而且变化很大，使得顺序存储结构的最大长度难以确定。特别是在处理式子的次数很高变化很大，使得顺序存储结构的最大长度很难确定。特别是形如

$$S(x)=1+3x^10000+2x^20000$$
的多项式时，就要用一长度为20001的线性表来表示，表中却只有3个非0元素，这种对内存空间的浪费是应当要避免的，但是如果只存储非零系数则显然必须同时存储相应的指数。

一般情况下，一元n次多项式可以写成:

$$p_n(x)=p_1x^{e_1}+p_2x^{e_2}+p_3x^{e_3}+...+p_mx^{e_m}$$

$p_i$是指数为$e_i$的项的非零系数，且满足

$$0 \leq e_1 < e_2 <...<e_m = n$$

若是用一个长度为m且每个元素有两个数据项(系数项和指数项)的线性表

$$((p_1,e_1),(p_2,e_2),...,,(p_m,e_m))$$
便可唯一确定多项式 $P_n(x)$。
最坏情况下，n+1(=m)个系数都不为零，则比只存储每项系数的方案要多一倍的数据。但是对于前面涉及到的 $S（x）$类的多项式（式子的次数很高变化很大），将大大节省空间。

若只对多项式进行“求值”等不改变多项式系数和指数的运算，采用类似顺序表的顺序存储结构。否则，用链表结构。

抽象数据类型一元多项式定义

ADT Polynomial{
数据对象：D＝{ ai | ai∈TermSet, i=1,2,...,m,  m≥0 
TermSet中的每个元素包含一个表示系数的实数和表示指数的整数}
数据关系：R1＝{ <ai-1, ai>|ai-1, ai∈D, 且ai-1中的指数值<ai中的指数值，i=2，……，n}
基本操作：
     CreatPolyn（&P，m）
操作结果：输入m项的系数和指数，建立一元多项式P。
     DestroyPolyn（&P）
初始条件：一元多项式P已存在。
操作结果：销毁一元多项式P。
     PrintPolyn（P）
初始条件：一元多项式P已存在。
操作结果：打印输出一元多项式P。
     PolynLength（P）
初始条件：一元多项式P已存在。
操作结果：返回一元多项式P中的项数。
    AddPolyn（&Pa，&Pb）
初始条件：一元多项式Pa和Pb已存在。
操作结果：完成多项式相加运算，即：Pa=Pa+Pb，并销毁一元多项式Pb。
    SubtractPolyn(&Pa,&Pb)
初始条件：一元多项式Pa和Pb已存在。
操作结果：完成多项式相减运算，即：Pa=Pa-Pb，并销毁一元多项式Pb。
    MultiplyPolyn(&Pa,&Pb)
初始条件：一元多项式Pa和Pb已存在。
操作结果：完成多项式相乘运算，即：Pa=Pa×Pb，并销毁一元多项式Pb。
}ADT Polynomial

实现此定义，需要采用链式存储结构

相加如何实现？

一元多项式相加原则：对于两个一元多项式中所有指数相同的项，对应系数相加，若其和不为零，则构成“和多项式“中的一项,对于两个一元多项式中所有指数不相同的项，则分别复抄写到”和多项式“中去。

按照Polynomial定义，”和多项式“链表中的结点无需另外生成，而应从两个多项式的链表中摘取。

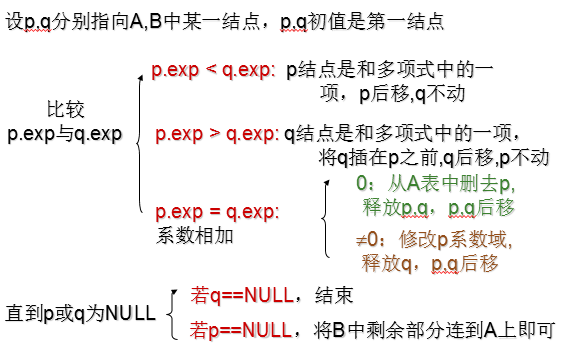
运算规则:
假设指针qa和qb分别指向多项式A和多项式B中当前进行比较的某个结点，则想比较两个结点中的指数值。存在下列的三种情况：

结语

下一文章将会给出如何实现一元多项式相加，此节则给大家建立一元多项式相加的想法。