电容的本质是一个容器。就好像一个蓄水池，既能存水，又能从中取水；又好像一个储钱罐子，既能存钱，又能从中取钱。

1 ‘藏’        

        存储电荷的容器，称为电容。

        所有传递给电阻的能量都以热量的形式被消耗掉，但是电容不会。

        所以，电容是一个储能元件。

        这种特性，我将其描述为一个字：“藏”。

        电容的一切应用，都源自于“储藏”。

2 基础公式与推论

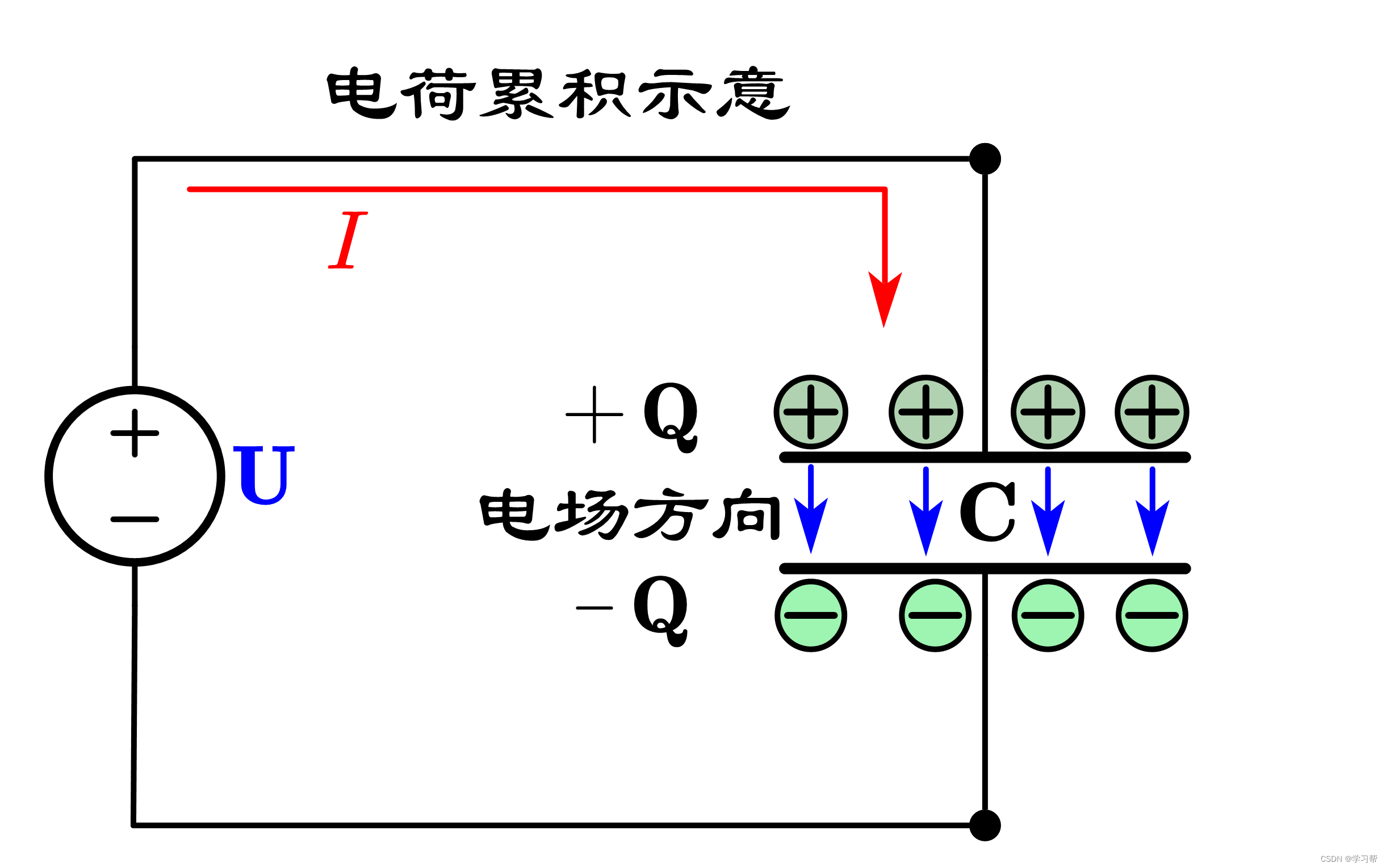
        任意两块平行金属板就能构成一个简易电容器。给极板两侧通上电的瞬间便完成了电荷的“储藏”过程，使得上极板充满正电荷，下极板全是负电荷。

        储藏的电荷来自于电源，极板电容两端的电压越大，储藏的电荷越多。

        “储藏”电荷需要一定的时间，该过程的电荷移动形成了电流。

        在极短的时间内，电荷移动产生了多少电流？结合微积分，便有了电容的核心公式：

        核心公式的直观理解与推论：

• 电容越大，储藏的电荷就越多，因而可以提供更多的电流

推论1：电容可以用做负载的电流小金库，以备不时之需
推论2：电容可视为一个小型电荷泵，电荷取用自由

• 电压变化地越快，得到的电流就越大

推论3：电路上下电瞬间，电压突变，导致电容两端的电流突变
推论4：由电路上下电造成的电流尖峰，称之为浪涌电流

• 电流的大小取决于电容两端电压的变化率，和电容本身大小无关

解释：电容一旦制作完成，其容值便基本固定，因此dv/dt起决定作用

        进一步推导出电容“储藏”的能量：

        基于直流电源基础上的公式推导，如上文所述。

        如果面对的是交流电，此时的公式是否会产生某些变化？

        将正弦交流电压，带入核心公式，可得到电流的交流形式：

        运用欧姆定理，便得到电容的容抗表达式：

        从容抗表达式，能看出：

• 通高频，通交流

解释：当处于高频交流电路中时，容抗X十分小，不具有“抵抗”作用，很容易通过

• 阻低频，阻直流

解释1：低频电路，容抗X特别大，“抵抗”力十足，将低频信号隔绝在外
解释2：直流，是频率为0的交流信号

3 高频模型

        为简化计算，运用理想平行板电容模型参与简单计算。

        受到实际生产制造工艺的局限，真实电容带有许多寄生参数。这些寄生参数在高频中会带来较大的影响，难以忽略。

        如填充在极板间的介质很难做到完全绝缘；如存在于引线上的电阻/电感等......

        应用中，会综合考虑这些寄生参数，用等效串联电阻ESR模拟参数中的阻性；用等效串联电感ESL模拟参数中的感性。这两个参数会带来一定的损耗，如漏电流等。

        从高频阻抗公式，能看出：

• 电容介质损耗

        引入3种功率，储存功率（无功功率Q）,消耗功率（有功功率P），视在功率S，三种功率组成功率三角形，如上图所示。引出电容介质损耗：

• 谐振频率点

        从公式可以看到：

1谐振点处，电容呈现纯阻性
2影响谐振频率的参数，主要是ESL和容值
3显然容值越大，谐振频率越小（和容值相比，ESL的数值几乎可以忽略）

        不同容值的阻抗频率曲线如图所示：

4 两组六大参数

        仿照电阻参数，本文将电容参数划分成2组，细分为6小个。分别是：

        物有形---封装、容值

        物有实---材料、温漂、精度、耐压

        容值刻度、以及耐压等参数通常会标注在插针式电容表面；而对于贴片式电容，由于表面积不足，因而只能看到简单的几何外形。

• 参数1：封装

        常见贴片式和插针式两种。贴片式的器件需要使用回流焊，插针式使用波峰焊进行焊接。对于贴片式的封装，又根据大小分为0805、0603等。

回流焊：使用高温热风使涂在焊盘表面的锡膏融化，进而形成焊点
波峰焊：一种手焊的机械自动化形式，用熔融态的锡去触碰针脚

• 参数2：容值

        容值的单位记忆小口诀，皮纳微法。每个字之间相差1000倍。

• 参数3：温漂

        同电阻一样，这是一个材料精度。容值随温度的变化率，单位ppm/℃。

• 参数4：精度

        纯正反映制造水平的参数，水平高，精度高。

• 参数5：耐压

        标称最大工作电压，和电容的尺寸、材料均有关。

• 参数6：材料

        以贴片式陶瓷电容为例，俗称MLCC。按材料特性可将其分为两类，第一类电容和第二类电容。

        第一类电容：代表C0G，适用于高频电路的滤波、耦合等，容值稳定可靠。

        第二类电容：代表X7R，稳定性较差，DC偏压特性差【电容量随直流电压的瞪大而减小】，此类电容命名以温度-精度著称，常见的几大类如下表所示：

5 RC积分电路

        RC电路是阻容系统中的最简形式。这个电路有两个变种，一种电容接地，一种电阻接地。山河主讲电容接地的变种，即RC积分电路。

        前面咱说，电容是一个水池。

        那么无论是从中取水，或者将水池装满，都需要一定的时间。

        时间常数具有如下定义，单位：秒，反映充放电的快慢

        阶段1：充电

        充电过程电压表达式，其图像恰如上图中绿色部分。

        从电压表达式，能了解到如下信息

1.充电开始的瞬间，电容两端电压为0，等价为导线，必然产生电流

2.充满电的时间大概是5τ，此时大概充到99.3%的程度

3.充电完成时，电容两端的电压约等于电源，视为电容开路

4.电压的主要变化过程，体现在第一个τ内

5.电容两端的电压是缓慢增加的

        上述就是“电容两端的电压不能突变”的原因。

        其实从公式Q=CU同样能推导出“电容两端的电压不能突变”，因为电荷的累积不可能一蹴而就。

        充电过程的电流表达式，其图像如下图橙色曲线所示

        从电流表达式，能了解到：

1.充电开始的瞬间，电容两端存在电流，即电压为0，电流不为0

2.初始电流尖峰，随充电时间增加而减小

        提个问题，上图中标记X处，为什么没有重合？即电流电压曲线起始点为何没有重合？

        因为，起始点处电容形同一根导线，因此导线中会有电路的电流。

                一旦充电开始，电容上会产生一个电流尖峰，称之为“浪涌电流”。

        除了“浪涌电流”外，还能看出一个概念，DC偏压特性。显然充电过程中，电压不断增加，电流不断减小。

        电流的减小，说明电容的容抗在增加。

        电压在增加，根据C=Q/U知，容值在动态减小，因此容抗在增加。

即，DC偏压特性是电容特有属性，但是X7R材质的电容相较于C0G的要差许多，也因此会有更陡峭的浪涌电流

        阶段2：放电

        放电过程就是充电的逆过程，电压仍然没有突变，浪涌电流仍然存在

        怎样统一充放电过程？

        其实很简单，之前我们一直假想的是从“0”开始充电，而这在实际应用中，几乎是不可能的。因此，就有了如下统一公式：

U0：初始电压，如果为0，就成了理想充电过程
U1：终点电压，如果为0，就成了理想放电过程

6 时间常数

        再来看看不同时间常数，对充放电电压/电流的影响。

        时间常数越小，充满电的时间越短，电压/电流的上升沿越陡峭，这将会带来两个影响，其一，引入较大的浪涌电流；其二，造成比较恶劣的EMC结果。

        时间常数过大，曲线上升缓慢，甚至在电压脉冲周期结束时，充电尚未完成就立马转入放电周期。这种现象会给后级电路带来纹波电压。

        另一方面，时间常数过大或者过小，都会导致后级ADC采样失准。即原本需要对1.2V采样，但因为时间常数的缘由，采集到的真实电压大于/小于1.2V，进而造成ADC采样转化上面的数值偏差。

        前文都是在假设电源频率不变的基础下，增大/减小时间常数，进而导致充放电曲线的缓/抖。

        换一个角度，时间常数固定不变，改变电源的频率，会发生什么？

        以实际应用中比较常见的场景，PWM信号的滤波电容，它的充放电波形是什么样的？

        即如下两个操作对充放电曲线而言是几乎等价的：

CASE1:PWM频率不变，增大时间常数

CASE2:时间常数不变，增大PWM频率

        能看到一个显著趋势：频率越快，电容输出电压的幅值越小。

        但是，一旦频率增加到截止频率时，输出电压将不会再有变化。

        这便是为什么RC积分电路，又被称作“低通滤波器”。低通，藏掉高频。

7 容值计算

        在大多数直流系统中，电源端进来的第二个单元就是滤波，那么这个电容的容值该如何设计呢？利用电荷量守恒建立方程，即：

        假设12V，30A，±1%纹波精度，纹波频率400kHz的直流系统，则其纹波电压为：

        纹波频率决定了电容的有效充放电时间，因此在占空比50%的电源系统中，电容的充电时间为:

        从而计算出电容的容值为：

        进一步考虑电容不同的选值系列，并考虑一定的冗余，确定最终的电容值。

• 电容容值选择偏大/偏小带来哪些影响？

        选大了，容器大了，能藏的东西更多了，呈现出来就是纹波更小，但是电容的价格也会随之上涨。
        选小了，容器小了，藏不住东西，一藏就满，一掏就空，呈现出来就是曲线的斜率大，容抗也大，由于ESR的存在，导致纹波电压大，更是会产生热量，导致电容寿命下降。

• 选不到自己想要的容值怎么办？

        跟电阻一样，将电容串并联以获取自己需要的容值。

8 电容的应用

        回到开头，电容善藏。

        电容最重要的应用，就是滤波、储能。前者藏无用，后者藏有用。