1 引言

普通遗传算法（Sample Genetic Algorithm, SGA）存在着严重的缺点，它的Pc和Pm的值是固定的，本文采用自适应遗传算法进行求解TSP问题。不管是优良个体还是劣质个体都经过了相同概率的交叉和变异操作。这会引起两个很严重的问题：

1. 相同的概率，这可以说是不公平，因为对于优良个体，我们应该减小交叉变异概率，使之能够尽量保存 ； 而对于劣质个体，我们应该增大交叉变异概率，使之能够尽可能的改变劣质的状况 。所以，一成不变的交叉变异概率影响了算法的效率。
2. 相同的概率总不能很好的满足种群进化过程中的需要，比如在迭代初期，种群需要较高的交叉和变异概率，已达到快速寻找最优解的目的，而在收敛后期，种群需要较小的交叉和变异概率，以帮助种群在寻找完最优解后快速收敛。所以，一成不变的交叉变异概率影响了算法的效率。

2 旅行商问题（Travelling salesman problem，TSP）数学模型

刘兴禄 -《运筹优化常用模型、算法及案例实战：Python+Java实现》总结了TSP问题共有3种数学模型：

1. Dantzig-Fulkerson-Johnson model，DFJ模型（本文采用）
2. Miller-Tucker-Zemlin model，MTZ模型
3. 1-tree模型

DFJ模型，也是最常见的模型如下：
min ⁡ ∑ i ∈ V ∑ j ∈ V d i j x i j subject to ∑ j ∈ V x i j = 1 , ∀ i ∈ V , i ≠ j ∑ i ∈ V x i j = 1 , ∀ j ∈ V , i ≠ j ∑ i ∈ S ∑ j ∈ S x i j ≤ ∣ S ∣ − 1 , 2 ≤ ∣ S ∣ ≤ N − 1 , S ⊂ V x i j ∈ { 0 , 1 } , ∀ i , j ∈ V \begin{align} \min \quad & \sum_{i \in V}{}\sum_{j \in V} d_{ij}x_{ij}\\ \text{subject to} \quad &\sum_{j \in V} x_{ij} = 1, \quad \forall i \in V,i \neq j \\ &\sum_{i \in V}{x_{ij}} =1,\quad \forall j \in V ,i \neq j\\ & \textcolor{red}{\sum_{i\in S}\sum_{j \in S}{x_{ij}} \leq |S|-1,\quad 2\leq |S| \leq N-1, S \subset V}\\ &x_{ij} \in \{0,1\}, \quad \forall i,j \in V \end{align} minsubject to​i∈V∑​j∈V∑​dij​xij​j∈V∑​xij​=1,∀i∈V,i=ji∈V∑​xij​=1,∀j∈V,i=ji∈S∑​j∈S∑​xij​≤∣S∣−1,2≤∣S∣≤N−1,S⊂Vxij​∈{0,1},∀i,j∈V​​
另外以下文章总结了TSP几种建模方式的详细介绍，包括各种模型优劣：

• TSP几种建模方式
• DFJ和MTZ模型介绍
• DFJ和MTZ模型求解能力对比

3 遗传算法求解TSP问题

3.1初始种群生成

种群规模设置为100，随机城市顺序，采用自然数编码方式构造染色体，用0-19表示20个城市，染色体的编码如图所示，每条染色体表示城市访问顺序。如下图表示为：该旅行商从城市2出发，走到城市8，最后回到城市2。

3.2适应度计算

适应度函数是非负的，任何情况下总希望越大越好。TSP问题的目标函数是总距离越小越好，所以设计适应度函数为 $fitness=\frac{1}{z}$

3.3 选择操作（精英策略+轮盘赌策略）

精英策略：即选择父代中适应度最大的个体遗传到子代。
轮盘赌选择：计算产生新个体的适应值，根据适应值大小分配个体的概率，根据概率方式选择个体作为下一代种群的父代。基本思想：各个个体被选中的概率与其适应度大小成正比,适应度值越好的个体，被选择的概率就越大。轮盘赌选择步骤如下：

1. 计算适应度：适应度为该条染色体（一条可行路径）的总距离的倒数
2. 计算每个个体的选择概率：选择概率是个体被遗传到下一代的概率，显然适应度愈大，该个体愈能适应环境，遗传到下一代的概率更高。染色体$i$的选择概率计算公式为$p_i(select)=\frac{fitnes{s}_i}{{\sum }_{i=1}^{N}fitnes{s}_i}$ ，其中$i$代表个体，$N$代表种群规模。
3. 计算每个个体的累积概率：$p_i(cul)={\sum }_{j=1}^i{p}_j(select)$
4. 执行精英策略：在当代种群population中把选择概率最大的个体，直接复制到子代种群offspring，即offspring[1] = population[argmax(p_select)]，其中p_select= { p i ( s e l e c t ) } i = 1 N \{p_i(select)\}_{i=1}^N {pi​(select)}i=1N​
5. 执行轮盘赌选择：对每个个体$i$，在[0, 1]区间生成一个随机数$r_i$，若$p_{i-1}(cul)\le r_i\le p_i(cul)$，则个体i被选择至下一代。
6. 重复步骤5，N-1次。

3.4 交叉

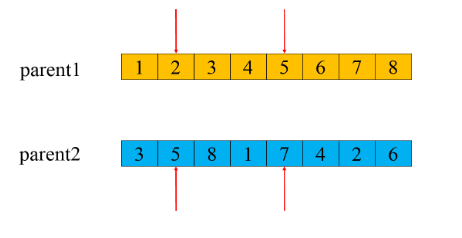
选择两点交叉（Two-points crossover）作为本文的交叉算子，两点交叉步骤如下：

1. 随机选择两条染色体作为父代染色体，随机选择交叉基因的起止位置（两染色体被选位置相同）。

2. 交换这两组基因的位置。

3. 重复基因检测根据交换的两组基因建立一个映射关系（映射表），如图所示，以7-5-2这一映射关系为例，可以看到第二步结果中子代1存在两个基因7，这时将其通过映射关系转变为基因2，以此类推至没有冲突为止。最后所有冲突的基因都会经过映射，保证形成的新一对子代基因无冲突。

4. 重复基因替换。对非交叉的基因片段进行扫描，若发现重复基因，则根据step3建立的映射表进行替换。保证了每个染色体中的基因仅出现一次，通过该交叉策略在一个染色体中不会出现重复的基因，所以经常用于旅行商（TSP）或其他排序问题编码。

3.5 变异

采用2-opt方法，即随机选择一条染色体，随机选择2个基因位，将这两个位置的基因交换，如下图。

3.6 停止准则

停止准则有3种，本文选择第三种。

1. 当最优个体的适应度达到给定的阈值
2. 最优个体的适应度和群体适应度不再上升
3. 迭代次数达到预设的代数时，算法终止（本文采用）

4 数值实验

20个城市的TSP问题，每个城市的坐标如下（city20.txt）：

60,200
180,200
80,180
140,180
20,160
100,160
200,160
140,140
40,120
100,120
180,100
60,80
120,80
180,60
20,40
100,40
200,40
20,20
60,20
160,20

程序包括以下几个类：

1. GeneticAlgorithm遗传算法
2. Main运行
3. TSP读取文件（20个城市的坐标，）
4. Node城市

C:.
│  .gitignore
│  pom.xml
│  project_structure.txt
│  
├─.idea
│  │  .gitignore
│  │  compiler.xml
│  │  encodings.xml
│  │  jarRepositories.xml
│  │  misc.xml
│  │  uiDesigner.xml
│  │  workspace.xml
│  │  
│  └─artifacts
│          unnamed.xml
│          
├─src
│  └─main
│      │  att48.txt
│      │  city20.txt
│      │  eil51.txt
│      │  
│      ├─java
│      │  └─org
│      │      └─example
│      │              Main.java
│      │                  GeneticAlorithm
│      │                  Main
│      │                  Node
│      │                  TSP
│      │              
│      └─resources

pom.xml：

<?xml version="1.0" encoding="UTF-8"?>
<project xmlns="http://maven.apache.org/POM/4.0.0"
         xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"
         xsi:schemaLocation="http://maven.apache.org/POM/4.0.0 http://maven.apache.org/xsd/maven-4.0.0.xsd">
    <modelVersion>4.0.0</modelVersion>

    <groupId>org.example</groupId>
    <artifactId>adaptive_ga-tsp</artifactId>
    <version>1.0-SNAPSHOT</version>

    <properties>
        <maven.compiler.source>17</maven.compiler.source>
        <maven.compiler.target>17</maven.compiler.target>
        <project.build.sourceEncoding>UTF-8</project.build.sourceEncoding>
    </properties>
    <dependencies>
        <dependency>
            <groupId>org.apache.commons</groupId>
            <artifactId>commons-lang3</artifactId>
            <version>3.9</version>
        </dependency>

        <dependency>
            <groupId>org.apache.commons</groupId>
            <artifactId>commons-collections4</artifactId>
            <version>4.4</version>
        </dependency>
        <dependency>
            <groupId>org.apache.commons</groupId>
            <artifactId>commons-math3</artifactId>
            <version>3.6.1</version>
        </dependency>
        <dependency>
            <groupId>org.icepear.echarts</groupId>
            <artifactId>echarts-java</artifactId>
            <version>1.0.3</version>
        </dependency>
    </dependencies>
</project>

算法程序：基于自适应遗传算法的TSP问题建模求解（Java）

完整程序：

package org.example;

import org.apache.commons.math3.stat.StatUtils;
import org.icepear.echarts.Bar;
import org.icepear.echarts.render.Engine;

import java.io.BufferedReader;
import java.io.File;
import java.io.FileReader;
import java.io.IOException;
import java.nio.file.Files;
import java.nio.file.Paths;
import java.util.Arrays;
import java.util.HashSet;
import java.util.Set;
import java.util.concurrent.ThreadLocalRandom;

public class Main {
    public static void main(String[] args) throws IOException {
        String filepath = "src/main/att48.txt";
        filepath = "src/main/city20.txt";
        GeneticAlgorithm ga = new GeneticAlgorithm(filepath, 10000, 100);
        ga.runGA();
    }
}

class Node {
    int id;
    double x;
    double y;

    Node(int id, double x, double y) {
        this.id = id;
        this.x = x;
        this.y = y;
    }
}

class TSP {

    public double[][] distance;

    public TSP(String fileName) throws IOException {
        distance = this.readFile_(fileName);
    }

    public double[][] readFile_(String filepath) throws IOException {
        int lineNum = (int) Files.lines(Paths.get(new File(filepath).getPath())).count();
        System.out.println(lineNum);
        Node[] nodes = new Node[lineNum];
        double[][] distance = new double[nodes.length][nodes.length];
        // 带缓冲的流读取，默认缓冲区8k
        try (BufferedReader br = new BufferedReader(new FileReader(filepath))) {
            String line;
            while ((line = br.readLine()) != null) {
                String[] data = line.split(" ");
                int id = Integer.parseInt(data[0]);
                int x = Integer.parseInt(data[1]);
                int y = Integer.parseInt(data[2]);
                Node node = new Node(id, x, y);
                nodes[id - 1] = node;
            }


        } catch (IOException e) {
            throw new RuntimeException(e);
        }

        for (int i = 0; i < nodes.length; i++) {
            distance[i][i] = 0;
            for (int j = 0; j < nodes.length; j++) {
                distance[i][j] = distance[j][i] = Math.sqrt(Math.pow(nodes[i].x - nodes[j].x, 2) + Math.pow(nodes[i].y - nodes[j].y, 2));
            }
        }
        return distance;
    }

}

class GeneticAlgorithm {
    TSP tsp;
    double[][] distance;//距离矩阵
    int popsize; //种群规模
    int num_city;//基因数量
    int[][] parent;//父代种群
    double[] fitness;//适应度
    int[][] child;//子代种群
    private final int GEN;//最大迭代次数
    private double pc = .8;//交叉概率
    private double pm = .2;//变异概率
    private final ThreadLocalRandom rand;

    public GeneticAlgorithm(String fileName, int maxgen, int popsize) throws IOException {
        this.distance = new TSP(fileName).distance;
        this.pc = 0.;
        this.pm = 0.;
        this.GEN = maxgen;
        this.popsize = 100;
        this.num_city = distance.length;
        this.parent = new int[popsize][];
        this.child = new int[popsize][num_city];
        this.fitness = new double[popsize];
        this.rand = ThreadLocalRandom.current();
    }

    /**
     * 初始化种群
     */
    private void initialize_pop() {
        for (int i = 0; i < this.popsize; i++) {
            parent[i] = rand.ints(0, num_city).distinct().limit(num_city).toArray();
        }
    }

    //适应度函数
    private void calc_fitness() {
        for (int i = 0; i < parent.length; i++) {
            fitness[i] = 1e6 / calc_path_distance(parent[i]);
        }

    }

    //更新交叉概率、变异概率
    private void update_pc_pm() {
        double fmax = StatUtils.max(fitness);           //最大适应度
        double favg = StatUtils.sum(fitness) / popsize; //平均适应度
        pc = 100 / (fmax - favg);
        pm = 100 / (fmax - favg);
    }

    /**
     * @param chrom 染色体
     * @return 一条染色体的总距离
     */
    private double calc_path_distance(int[] chrom) {
        double total_distance = 0;
        for (int k = 0; k < chrom.length - 1; k++) {
            int i = chrom[k];
            int j = chrom[k + 1];
            total_distance += distance[i][j];
        }
        total_distance += distance[chrom[chrom.length - 1]][0];
        return total_distance;
    }

    /**
     * 选择操作
     */
    private void selection() {
        //精英选择1条染色体
        double max_fitness = StatUtils.max(fitness);
        int elite = 0;
        for (int i = 0; i < fitness.length; i++)
            if (max_fitness == fitness[i]) {
                elite = i;
                break;
            }
        System.arraycopy(parent[elite], 0, child[0], 0, num_city);
        //轮盘赌选择99条染色体
        this.roulette_select();
    }

    /**
     * 轮盘赌选择
     */
    private void roulette_select() {
        double[] p_cum = cumsum();
        for (int i = 1; i < popsize; i++) {
            double r = Math.random();
            int selected = 0;
            for (int j = 0; j < p_cum.length; j++) {
                if (r < p_cum[j]) {
                    selected = j;//选择第j条染色体
                    break;
                }
            }
            System.arraycopy(parent[selected], 0, child[i], 0, num_city);
        }
    }


    //累积概率
    private double[] cumsum() {
        double[] p_cum = new double[popsize];
        double[] p_select = calc_select_prob();
        for (int i = 0; i < popsize; i++) {
            double temp = 0.;
            for (int j = 0; j <= i; j++) {
                temp += p_select[j];
            }
            p_cum[i] = temp;
        }
        return p_cum;
    }

    //选择概率
    private double[] calc_select_prob() {
        double[] p_select = new double[popsize];
        for (int i = 0; i < popsize; i++)
            p_select[i] = fitness[i] / Arrays.stream(fitness).sum();
        return p_select;
    }

    public void crossover() {
        // 选择父代染色体
        int i = rand.nextInt(1, popsize);
        int j = rand.nextInt(1, popsize);
        int[] parent1 = this.parent[i];
        int[] parent2 = this.parent[j];
        // 生成子代染色体
        int[] child = new int[num_city];
        // 选择交叉位置
        int start = rand.nextInt(0, num_city);
        int end = rand.nextInt(start, num_city);

        int[] arr = Arrays.copyOfRange(parent1, start, end);
        System.arraycopy(parent1, start, child, start, end - start);

//        int p = 0;
//        for (int k = 0; k < start; ) {
//            if (!contain(arr, parent[j][p])) {
//                child[k] = parent[j][p];
//                k++;
//            }
//            p++;
//        }
//
//        for (int k = end; k < num_city; ) {
//            if (!contain(arr, parent[j][p])) {
//                child[k] = parent[j][p];
//                k++;
//            }
//            p++;
//        }
        for (int k = 0, left = 0, right = end; k < num_city; k++) {
            if (!contains(arr, parent2[k])) {
                if (left < start) {
                    child[left] = parent2[k];
                    left += 1;
                } else if (right < num_city) {
                    child[right] = parent2[k];
                    right += 1;
                }
            }
        }
        this.child[i] = child;

    }

    boolean contains(int[] arr, int element) {
        for (int j : arr) {
            if (element == j) {
                return true;
            }
        }
        return false;
    }

    /**
     * 变异操作
     */
    public void mutation() {
        //i从1开始 保留精英
        for (int i = 1; i < child.length; i++) {
            int r1 = rand.nextInt(0, num_city);
            int r2 = rand.nextInt(0, num_city);
            int gene1 = child[i][r1];
            int gene2 = child[i][r2];


            child[i][r1] = gene2;
            child[i][r2] = gene1;
        }
    }


    public void runGA() {
        initialize_pop();
        calc_fitness();
        int[] gbest = parent[0];
        long start = System.currentTimeMillis();
        for (int gen = 0; gen <= GEN; gen++) {
            selection();
            crossover();
            mutation();
            for (int i = 0; i < child.length; i++) {
//                parent[i] = child[i];
                System.arraycopy(child[i], 0, parent[i], 0, num_city);
            }
            gbest = child[0];
            for (int i = 0; i < child.length; i++) {
                if (isRepetition(child[i])) {
                    System.out.println(Arrays.toString(child[i]));
                    throw new IllegalArgumentException("repetition!");
                }
            }
            calc_fitness();
            if (gen % 200 == 0) {
                System.out.printf("iteration: %d, path: %s, distance: %s\n", gen, Arrays.toString(gbest), calc_path_distance(gbest));
            }
        }
        long end = System.currentTimeMillis();
        System.out.printf("time used: %ss", (end - start) / 1000);
    }

    static boolean isRepetition(int[] args) {
        Set<Object> set = new HashSet<>();
        for (int arg : args) set.add(arg);
        return set.size() != args.length;
    }


}

迭代10000次结果如下，800多就逼近最优解：

Iteration: 0 path: [11, 17, 4, 2, 15, 10, 14, 18, 7, 12, 19, 8, 9, 5, 3, 1, 6, 16, 13, 0] distance: 1729.0
Iteration: 200 path: [15, 18, 17, 14, 11, 8, 4, 2, 9, 12, 13, 10, 7, 5, 3, 1, 6, 16, 19, 0] distance: 1122.0
Iteration: 400 path: [15, 18, 17, 14, 11, 8, 4, 2, 9, 12, 19, 16, 13, 10, 6, 1, 3, 7, 5, 0] distance: 893.0
Iteration: 600 path: [15, 18, 17, 14, 11, 8, 4, 5, 9, 12, 19, 16, 13, 10, 6, 1, 3, 7, 2, 0] distance: 887.0
Iteration: 800 path: [15, 18, 17, 14, 11, 8, 4, 5, 9, 12, 19, 16, 13, 10, 6, 1, 3, 7, 2, 0] distance: 887.0
Iteration: 1000 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 1200 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 1400 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 1600 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 1800 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 2000 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 2200 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 2400 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 2600 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 2800 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 3000 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 3200 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 3400 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 3600 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 3800 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 4000 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 4200 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 4400 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 4600 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 4800 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 5000 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 5200 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 5400 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 5600 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 5800 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 6000 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 6200 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 6400 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 6600 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 6800 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 7000 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 7200 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 7400 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 7600 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 7800 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 8000 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 8200 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 8400 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 8600 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 8800 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 9000 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 9200 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 9400 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 9600 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 9800 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
Iteration: 10000 path: [15, 18, 17, 14, 11, 8, 4, 9, 7, 12, 19, 16, 13, 10, 6, 1, 3, 5, 2, 0] distance: 879.0
time used: 1s