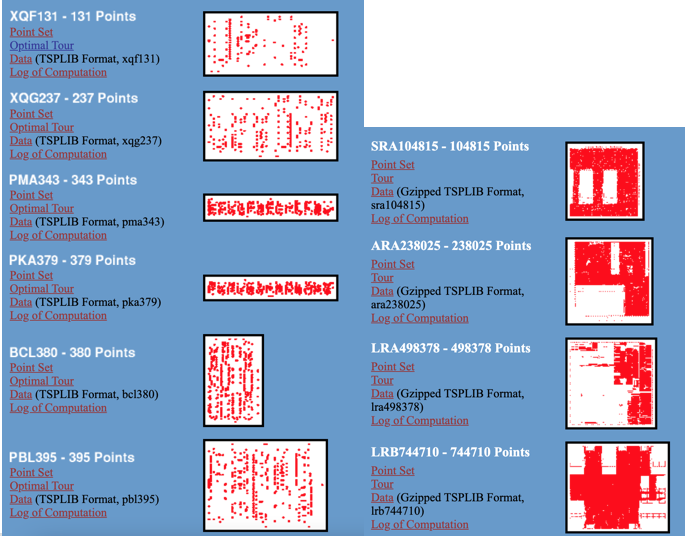
1 VLSI系列

从小规模到大规模都有，一共102个，点数从131到744,710，测试时可以使用此案例，地址为：http://www.math.uwaterloo.ca/tsp/vlsi/index.html。所有case的下载地址为：http://www.math.uwaterloo.ca/tsp/vlsi/vlsi_tsp.tgz

最优解的情况见http://www.math.uwaterloo.ca/tsp/vlsi/summary.html

2 National TSP

从只有29个城市的西撒哈拉，到71009个城市的中国，地址为http://www.math.uwaterloo.ca/tsp/world/，下面这个页面是25个城市的例子：http://www.math.uwaterloo.ca/tsp/world/countries.html，最优解的清单见http://www.math.uwaterloo.ca/tsp/world/summary.html

3 world TSP

见http://www.math.uwaterloo.ca/tsp/world/index.html。这个问题一共有1,904,711个城市，注意位置使用的是经纬度，距离使用TSPLIB GEO-norm方法计算。目前最佳的解是7,515,755,956，由Keld Helsgaun于2021年2月15日计算得到。目前的lower bound是2007年6月5日由concorde软件获得7,512,218,268.，GAP仅为0.0471%。

4 Monalisa problem

介绍网址：http://www.math.uwaterloo.ca/tsp/data/ml/monalisa.html
tsp问题下载地址：http://www.math.uwaterloo.ca/tsp/data/ml/mona-lisa100K.tsp
目前最优解是2009年3月17日,由Yuichi Nagata找到的，地址为：http://www.math.uwaterloo.ca/tsp/data/ml/tour/monalisa_5757191.tour，使用的是自己设计的遗传算法。结果保存在tour-5757191.npy中。已知的lower bound为5,757,084，Gap为107 (0.0019%)
不过，目前的结果有一个问题，大伙似乎在计算距离时用了四舍五入取整，因为Yuichi Nagata结果的总距离似乎是5759971.494762552，而不是5757191。如果保持5757191不变，我们可以调整路径，使得实际的总距离变为5759948.61713057，结果保存在tour-03060905.npy
使用ALNS算法，这个结果还可以继续优化，总距离为5759921.739287255，round之后的距离为5757225。结果保存在tour-0322.npy中。

下面是Monalisa问题的创造方法：
将灰度图片先转为离散图，然后将离散图用一笔画画出来。这里是创建离散图的一个python代码：https://github.com/ReScience-Archives/Rougier-2017

转为离散点的方法，使用的是weighted Voronoi stippling方法，参考这篇论文：https://www.cs.ubc.ca/labs/imager/tr/2002/secord2002b/secord.2002b.pdf
这里有一个重要的概念：抖动(dithering)。比如下图，实际只用了红蓝两种颜色，但是随着像素的变小，图片逐渐呈现出紫色。dithering是一种用随机误差来缓解系统误差的方式。

thresholding是将灰度图抖动为黑白图的最简单方法，用阈值进行像素的四舍五入。这种方法由于边界清晰，会产生明显的锯齿和色带问题。
grid distribution计算每一个grid中的平均灰度，以此为概率，对每个像素点进行采样。本质上是用grid代替像素来模拟灰度，让图片显示更自然。
Floyd-Steinberg dithering可以大幅降低需要的点数，这个方法使用如下的error diffusion method迭代进行thresholding：


当然还有很多其他的error diffusion method，下面是效果图：

Weighted Voronoi Stippling通过类似聚类的方式，让散点看起来更加“organized”。从标准网格或者随机分布点或者按照启发式规则生成的散点开始，计算Voronoi图，然后不断将各个块的中心点移动到质心（用顶点计算即可），接着重复计算Voronoi图、移动质心……；一般15次左右就可以收敛了。

5 TSPLIB

使用tspib库可以直接使用如下数据：
数据集名称：最优距离

a280 : 2579
ali535 : 202339
att48 : 10628
att532 : 27686
bayg29 : 1610
bays29 : 2020
berlin52 : 7542
bier127 : 118282
brazil58 : 25395❌
brd14051 : 469385
brg180 : 1950
burma14 : 3323
ch130 : 6110
ch150 : 6528
d198 : 15780
d493 : 35002
d657 : 48912
d1291 : 50801
d1655 : 62128
d2103 : 80450
d15112 : 1573084
d18512 : 645238
dantzig42 : 699
dsj1000 : 18659688 (EUC_2D)
dsj1000 : 18660188 (CEIL_2D)
eil51 : 426
eil76 : 538
eil101 : 629
fl417 : 11861
fl1400 : 20127
fl1577 : 22249
fl3795 : 28772
fnl4461 : 182566
fri26 : 937❌
gil262 : 2378
gr17 : 2085❌
gr21 : 2707❌
gr24 : 1272❌
gr48 : 5046❌
gr96 : 55209
gr120 : 6942
gr137 : 69853
gr202 : 40160
gr229 : 134602
gr431 : 171414
gr666 : 294358
hk48 : 11461
kroA100 : 21282
kroB100 : 22141
kroC100 : 20749
kroD100 : 21294
kroE100 : 22068
kroA150 : 26524
kroB150 : 26130
kroA200 : 29368
kroB200 : 29437
lin105 : 14379
lin318 : 42029
linhp318 : 41345
nrw1379 : 56638
p654 : 34643
pa561 : 2763
pcb442 : 50778
pcb1173 : 56892
pcb3038 : 137694
pla7397 : 23260728
pla33810 : 66048945
pla85900 : 142382641
pr76 : 108159
pr107 : 44303
pr124 : 59030
pr136 : 96772
pr144 : 58537
pr152 : 73682
pr226 : 80369
pr264 : 49135
pr299 : 48191
pr439 : 107217
pr1002 : 259045
pr2392 : 378032
rat99 : 1211
rat195 : 2323
rat575 : 6773
rat783 : 8806
rd100 : 7910
rd400 : 15281
rl1304 : 252948
rl1323 : 270199
rl1889 : 316536
rl5915 : 565530
rl5934 : 556045
rl11849 : 923288
si175 : 21407
si535 : 48450
si1032 : 92650
st70 : 675
swiss42 : 1273
ts225 : 126643
tsp225 : 3916
u159 : 42080
u574 : 36905
u724 : 41910
u1060 : 224094
u1432 : 152970
u1817 : 57201
u2152 : 64253
u2319 : 234256
ulysses16 : 6859
ulysses22 : 7013
usa13509 : 19982859
vm1084 : 239297
vm1748 : 336556