
BFS - C语言链表实现(简单易懂)
C语言链表实现BFS,从原理上讲解BFS。进阶讲解最短路径标记。
目录
1. BFS原理
1.1 BFS介绍
BFS(广度优先探索),与 DFS(深度优先探索) 相对应。形象地说,是一种从起点开始不断向外扩散搜索的一种搜索算法。

如图,黑色色块代表起点,灰色代表未搜索色块,灰白色代表已搜索色块,蓝色代表当前本轮搜索到的色块,绿色代表下一轮将搜索的色块,红色代表终点。
1.2 BFS如何实现?
(形象化描述)该算法中,首先需要一个 标记遍历的数组 ,记录已搜索过的地方。其次,对于本轮与下一轮的顺序处理,需要使用 队列 进行依次处理,这样保证了只有待上一轮处理完才会轮到下一轮处理。

对于本轮搜索的每一个元素,会将其从队首弹出并判断是否为终点,然后将符合搜索条件的下一轮元素从队尾入队,如果无符合搜索条件的下一轮元素,则无新的元素入队。若到搜索完毕都没发现终点,则不再有新的元素入队,最后一轮元素不断退队直至队列为空;若搜索到终点,则不再搜索, 队伍剩余元素不断退队直至队列为空。

总而言之,BFS是 顺序处理 上一轮与这一轮的元素,直至搜索到终点或再无符合搜索条件元素入队。
1.3 BFS处理逻辑 可视化
如今有一搜索范围,确定起点与终点。

初始化:初始化标记遍历都为 0;生成队列,将起点入队,标记为 1。
搜索条件:标记遍历不为 1,地图不为墙。
循环操作:(循环终止条件:队列为空)
(1) 将队首(此时为起点)弹出,并判断是否为终点(否,继续搜索)。
(2) 向四周查找符合搜索条件的元素,将这些元素逐个入队,标记为1。同时判断是否为终点(否,继续搜索)。

进入 下一个循环 :
(1) 将队首(此时为起点上方的元素)弹出,并判断是否为终点(否,继续搜索)。
(2) 向四周查找符合搜索条件的元素,将这些元素逐个入队,标记为1。判断是否为终点(否,继续搜索)。

......处理至下一轮并 继续循环 :


边界处:只将符合搜索条件的元素入队即可。

搜索到终点:停止继续搜索,不再有新元素入队,队列中剩余元素直接逐个出队直至空。
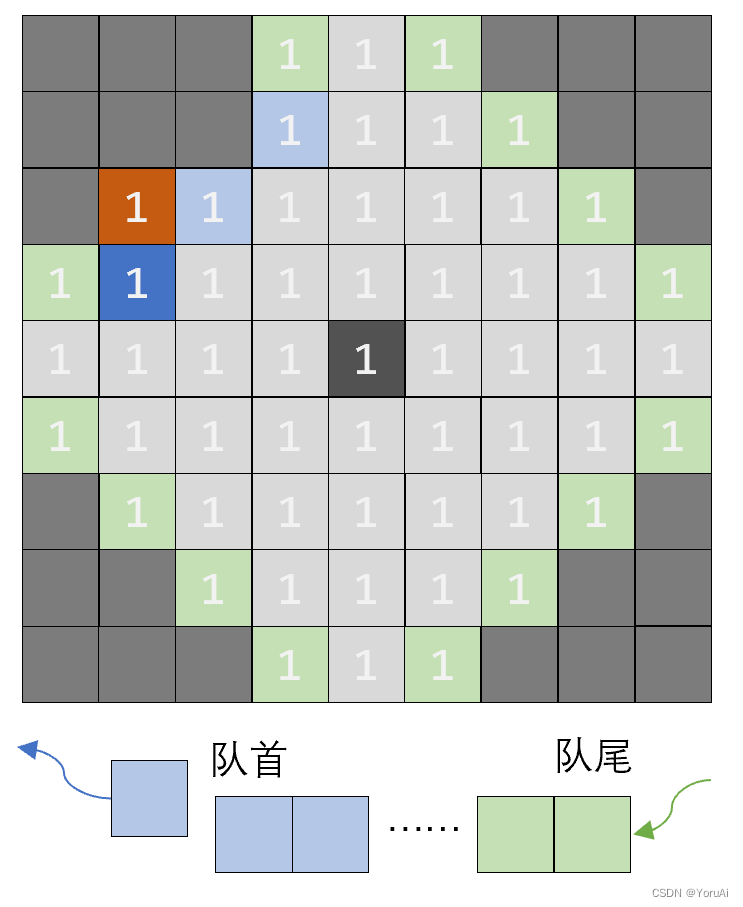
结束后:

2. C代码实现
2.1 队列(链表)
固定头节点 head
typedef struct node
{
// 坐标记录
int x;
int y;
// 第n轮搜索
int step;
// 链表链接
struct node *next;
} node;
// 头节点
node *head;入队
void push(node *newNode)
{
node *p = head;
// 遍历至队尾
while (p->next != NULL)
{
p = p->next;
}
// 链接
p->next = newNode;
}出队
void pop()
{
// 删除头节点下一节点
node *temp = head->next;
head->next = temp->next;
free(temp);
}2.2 前期准备
Map & Sign
#define ROW 8
#define COL 8
// ROW * COL Map
// 0为路径,1为墙,2为终点
int map[ROW + 2][COL + 2] = {
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 0, 0, 0, 0, 0, 0, 0, 1, 1},
{1, 1, 1, 1, 0, 1, 1, 1, 1, 1},
{1, 0, 0, 1, 0, 0, 1, 0, 1, 1},
{1, 0, 1, 0, 0, 1, 1, 0, 1, 1},
{1, 0, 1, 0, 1, 1, 1, 0, 1, 1},
{1, 0, 1, 0, 0, 0, 0, 0, 1, 1},
{1, 0, 0, 0, 1, 1, 1, 0, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 0, 2, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1}
};
int sign[ROW + 2][COL + 2] = {};方向
// += direction[i].x
// += direction[i].y
struct
{
int x;
int y;
} direction[4] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};2.3 BFS函数代码
// 以 x, y 坐标为起点
int bfs(int x, int y)
{
// 记录最小步数
int MinStep = 0;
// 记录是否已抵达终点
int flag = 0;
// 初始化头节点
head = (node *)malloc(sizeof(node));
head->next = NULL;
// 起点节点入队
node *start = (node *)malloc(sizeof(node));
start->x = x;
start->y = y;
start->step = 0;
start->next = NULL;
push(start);
// 标记遍历为 1
sign[x][y] = 1;
// 在地图上标记起点为 5
map[x][y] = 5;
do
{
// 提取队首(注意此时还未出队)
node *prevNode = head->next;
// 如果当前已找到终点,队首直接出队,不再继续搜索
if (flag)
{
pop();
continue;
}
// 未找到,继续搜索
int i;
for (i = 0; i < 4; ++i)
{
// 对四个方向进行搜索判断
// 新建节点存储待判断元素信息
node *newNode = (node *)malloc(sizeof(node));
newNode->x = prevNode->x + direction[i].x;
newNode->y = prevNode->y + direction[i].y;
newNode->step = prevNode->step + 1;
newNode->next = NULL;
// 若找到终点,标记后不再搜索
if (map[newNode->x][newNode->y] == 2)
{
flag = 1;
// 地图上标记为 3
map[newNode->x][newNode->y] = 3;
// 记录最小步数
MinStep = newNode->step;
free(newNode);
break;
}
// 若符合搜索条件,入队并标记
else if (sign[newNode->x][newNode->y] == 0 && map[newNode->x][newNode->y] == 0)
{
// 入队
push(newNode);
// 标记遍历为 1
sign[newNode->x][newNode->y] = 1;
// 地图上标记为 3
map[newNode->x][newNode->y] = 3;
}
// 不符合搜索条件
else
free(newNode);
}
// 此处的下一级元素全部入队后,队首出队
pop();
} while (head->next != NULL);
return MinStep;
}2.4 主函数输出
int main()
{
// 输出初始Map状态
int i, j;
for (i = 1; i <= ROW; ++i)
{
for (j = 1; j <= COL; ++j)
{
printf("%d ", map[i][j]);
}
putchar(10);
}
putchar(10);
// BFS 从 1,1 开始
int MinStep = bfs(1, 1);
// 输出最小步数
if (MinStep)
printf("MinStep = %d\n", MinStep);
else
printf("Not Found!");
for (i = 1; i <= ROW; ++i)
{
for (j = 1; j <= COL; ++j)
{
printf("%d ", map[i][j]);
}
putchar(10);
}
// 小心内存泄漏
free(head);
return 0;
}2.5 BFS总代码
#include <stdio.h>
#include <stdlib.h>
#define ROW 8
#define COL 8
typedef struct node
{
int x;
int y;
int step;
struct node *next;
} node;
node *head;
struct
{
int x;
int y;
} direction[4] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
int map[ROW + 2][COL + 2] = {
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 0, 0, 0, 0, 0, 0, 0, 1, 1},
{1, 1, 1, 1, 0, 1, 1, 1, 1, 1},
{1, 0, 0, 1, 0, 0, 1, 0, 1, 1},
{1, 0, 1, 0, 0, 1, 1, 0, 1, 1},
{1, 0, 1, 0, 1, 1, 1, 0, 1, 1},
{1, 0, 1, 0, 0, 0, 0, 0, 1, 1},
{1, 0, 0, 0, 1, 1, 1, 0, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 0, 2, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1}
};
int sign[ROW + 2][COL + 2] = {};
void push(node *newNode)
{
node *p = head;
while (p->next != NULL)
{
p = p->next;
}
p->next = newNode;
}
void pop()
{
node *temp = head->next;
head->next = temp->next;
free(temp);
}
int bfs(int x, int y)
{
int MinStep = 0;
int flag = 0;
head = (node *)malloc(sizeof(node));
head->next = NULL;
node *start = (node *)malloc(sizeof(node));
start->x = x;
start->y = y;
start->step = 0;
start->next = NULL;
push(start);
sign[x][y] = 1;
map[x][y] = 5;
do
{
node *prevNode = head->next;
if (flag)
{
pop();
continue;
}
int i;
for (i = 0; i < 4; ++i)
{
node *newNode = (node *)malloc(sizeof(node));
newNode->x = prevNode->x + direction[i].x;
newNode->y = prevNode->y + direction[i].y;
newNode->step = prevNode->step + 1;
newNode->next = NULL;
if (map[newNode->x][newNode->y] == 2)
{
flag = 1;
map[newNode->x][newNode->y] = 3;
MinStep = newNode->step;
free(newNode);
break;
}
else if (sign[newNode->x][newNode->y] == 0 && map[newNode->x][newNode->y] == 0)
{
push(newNode);
sign[newNode->x][newNode->y] = 1;
map[newNode->x][newNode->y] = 3;
}
else
free(newNode);
}
pop();
} while (head->next != NULL);
return MinStep;
}
int main()
{
int i, j;
for (i = 1; i <= ROW; ++i)
{
for (j = 1; j <= COL; ++j)
{
printf("%d ", map[i][j]);
}
putchar(10);
}
putchar(10);
int MinStep = bfs(1, 1);
if(MinStep)
printf("Min step = %d\n", MinStep);
else
printf("Not Found!");
for (i = 1; i <= ROW; ++i)
{
for (j = 1; j <= COL; ++j)
{
printf("%d ", map[i][j]);
}
putchar(10);
}
free(head);
return 0;
}2.6 运行结果演示

3. 进阶:如何标记路径?
3.1 思路
首先,要求记录每一子节点的父节点。
于是,应在结构体中增加父节点指针。
typedef struct node
{
struct node *prev; // 父节点
int x;
int y;
int step;
struct node *next;
} node;其次,所有入队节点应保留用于回溯查询。
于是,不能弹出队首,应将指针指向下一节点。

最后,要记得 free 防止内存泄漏哦!
void quit()
{
while (head->next != NULL)
{
node *temp = head->next;
head->next = temp->next;
free(temp);
}
free(head);
head = NULL;
}3.2 最短路径标记的实现
从终点开始不断向前找父节点直至 NULL 。
void route()
{
node *p = head;
// 遍历到队尾(终点节点)
while (p->next != NULL)
{
p = p->next;
}
// 从终点节点的上一节点开始向前寻找路径(父节点)
p = p->prev;
while (p->prev != NULL)
{
// 在地图上标记为 4
map[p->x][p->y] = 4;
// 向前到父节点
p = p->prev;
}
}3.3 BFS路径标记总代码
#include <stdio.h>
#include <stdlib.h>
#define ROW 8
#define COL 8
// 高亮显示
#define Green "\033[1;32m"
// 清除高亮
#define None "\033[m"
typedef struct node
{
struct node *prev;
int x;
int y;
int step;
struct node *next;
} node;
node *head;
struct
{
int x;
int y;
} direction[4] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
int map[ROW + 2][COL + 2] = {
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 0, 0, 0, 0, 0, 0, 0, 1, 1},
{1, 1, 1, 1, 0, 1, 1, 1, 1, 1},
{1, 0, 0, 1, 0, 0, 1, 0, 1, 1},
{1, 0, 1, 0, 0, 1, 1, 0, 1, 1},
{1, 0, 1, 0, 1, 1, 1, 0, 1, 1},
{1, 0, 1, 0, 0, 0, 0, 0, 1, 1},
{1, 0, 0, 0, 1, 1, 1, 0, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 0, 2, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1}
};
int sign[ROW + 2][COL + 2] = {};
void push(node *newNode)
{
node *p = head;
while (p->next != NULL)
{
p = p->next;
}
p->next = newNode;
}
void quit()
{
while (head->next != NULL)
{
node *temp = head->next;
head->next = temp->next;
free(temp);
}
free(head);
head = NULL;
}
void route()
{
node *p = head;
while (p->next != NULL)
{
p = p->next;
}
p = p->prev;
while (p->prev != NULL)
{
map[p->x][p->y] = 4;
p = p->prev;
}
}
int bfs(int x, int y)
{
int flag = 0;
head = (node *)malloc(sizeof(node));
head->next = NULL;
node *start = (node *)malloc(sizeof(node));
// 初始化 start 节点的父节点为 NULL 用于终止路径标记
start->prev = NULL;
start->x = x;
start->y = y;
start->step = 0;
start->next = NULL;
push(start);
sign[x][y] = 1;
map[x][y] = 5;
node *prevNode = head;
do
{
// 指向下一节点
prevNode = prevNode->next;
if (flag)
continue;
int i;
for (i = 0; i < 4; ++i)
{
node *newNode = (node *)malloc(sizeof(node));
// 记录父节点
newNode->prev = prevNode;
newNode->x = prevNode->x + direction[i].x;
newNode->y = prevNode->y + direction[i].y;
newNode->step = prevNode->step + 1;
newNode->next = NULL;
if (map[newNode->x][newNode->y] == 2)
{
flag = 1;
// 终点节点入队
push(newNode);
break;
}
else if (sign[newNode->x][newNode->y] == 0 && map[newNode->x][newNode->y] == 0)
{
push(newNode);
sign[newNode->x][newNode->y] = 1;
map[newNode->x][newNode->y] = 3;
}
else
free(newNode);
}
} while (prevNode->next != NULL);
// 前进直至终点节点
// 输出终点节点步数
return prevNode->step;
}
int main()
{
// 便于之后高亮显示,否则会乱码
system("cls");
int i, j;
for (i = 1; i <= ROW; ++i)
{
for (j = 1; j <= COL; ++j)
{
printf("%d ", map[i][j]);
}
putchar(10);
}
putchar(10);
int MinStep = bfs(1, 1);
// 标记最短路径
route();
if(MinStep)
printf("Min step = %d\n", MinStep);
else
printf("Not Found!");
for (i = 1; i <= ROW; ++i)
{
for (j = 1; j <= COL; ++j)
{
// 高亮显示路径
if (map[i][j] == 4)
printf(Green "%d " None, map[i][j]);
else
printf("%d ", map[i][j]);
}
putchar(10);
}
// 防止内存泄漏
quit();
return 0;
}3.4 运行结果演示

4. 总结
BFS广度优先算法的实现要注意入队与出队时机、循环结束条件以及继续搜索条件。
试试看自己写一遍,想想如果想以矩形方式扩散搜索该怎么实现呢?(如下图)

(文中代码皆已经过编译运行)
文章为本人原创,创作不易,感谢支持!

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容





所有评论(0)