【金融、量化系列】计算股票历史期望收益率(年化)、收益率标准差(年化)、夏普比率、以及股票之间月收益率的相关系数,并以夏普比率、相关系数为条件筛选股票
使用akshare获取股票数据,利用月度数据计算每只上证50成分股的股票历史期望收益率(年化)、收益率标准差(年化)、夏普比率、以及股票之间月收益率的相关系数,并以夏普比率、相关系数为条件筛选股票。挑选5只股票组成篮子,篮子股票必须满足下列三个条件: A)过去3年的夏普比率大于0.2; B)过去1年的夏普比率大于0.1; C)这5只股票彼此之间的相关系数之和最小。
使用akshare获取股票数据,利用月度数据计算每只上证50成分股的股票历史期望收益率(年化)、收益率标准差(年化)、夏普比率、以及股票之间月收益率的相关系数,并以夏普比率、相关系数为条件筛选股票。挑选5只股票组成篮子,篮子股票必须满足下列三个条件: A)过去3年的夏普比率大于0.2; B)过去1年的夏普比率大于0.1; C)这5只股票彼此之间的相关系数之和最小。
目录
获取三年间每个月的无风险利率rf,选取当月末十年期国债收益率为准,若非交易日则另选一天:
计算期望收益率 E(ri)=rf+β(E(rm)−rf):
挑选5只股票组成篮子,篮子股票必须满足下列三个条件: A)过去3年的夏普比率大于0.2; B)过去1年的夏普比率大于0.1; C)这5只股票彼此之间的相关系数之和最小。
1 获取数据
import akshare as ak
SH50_codes = [600000,600028,600030,600031,600036,600048,600050,600104,600196,600276,600309,600436,600438,600519,600547,600570,600585,
600588,600690,600745,600809,600837,600887,600893,600900,601012,601066,601088,601138,601166,601211,601288,601318,601336,
601398,601601,601628,601633,601668,601688,601728,601857,601888,601899,601919,601995,603259,603288,603501,603986]
SH50_codes = list(map(str,SH50_codes))
SH50_quotations_dic = {}
for i in SH50_codes:
SH50_quotations_dic[i] = ak.stock_zh_a_hist(symbol=i, period='monthly', start_date="20190101", end_date='20211231', adjust="")
SH50_quotations_dic['600000']数据预览:
日期 开盘 收盘 最高 最低 成交量 成交额 振幅 涨跌幅 涨跌额 换手率 年化期望收益率 0 2019-01-31 9.74 10.73 10.73 9.58 4404194 4.490181e+09 11.73 9.49 0.93 1.57 73.959513 1 2019-02-28 10.82 11.74 12.15 10.62 5315299 6.002415e+09 14.26 9.41 1.01 1.89 93.274971 2 2019-03-29 11.81 11.28 12.38 10.90 9530781 1.102880e+10 12.61 -3.92 -0.46 3.39 31.214703 3 2019-04-30 11.36 11.97 12.20 11.28 12043355 1.408016e+10 8.16 6.12 0.69 4.29 34.030901 4 2019-05-31 11.75 11.13 11.94 10.95 9505417 1.080917e+10 8.27 -7.02 -0.84 3.38 -63.805606 5 2019-06-28 11.17 11.68 12.32 11.13 8190692 9.600306e+09 10.69 4.94 0.55 2.91 65.973455 6 2019-07-31 11.86 11.87 12.00 11.22 6938976 8.059537e+09 6.68 1.63 0.19 2.47 -4.536585 7 2019-08-30 11.76 11.28 11.85 10.97 6956391 7.886875e+09 7.41 -4.97 -0.59 2.48 -11.354091 8 2019-09-30 11.30 11.84 12.18 11.24 6776832 8.007390e+09 8.33 4.96 0.56 2.41 8.588689 9 2019-10-31 11.80 12.51 13.33 11.80 10874626 1.386751e+10 12.92 5.66 0.67 3.87 18.232174 10 2019-11-29 12.50 11.91 13.19 11.89 8104901 1.004877e+10 10.39 -4.80 -0.60 2.88 -17.046202 11 2019-12-31 11.96 12.37 12.55 11.70 6476828 7.865092e+09 7.14 3.86 0.46 2.30 52.115898 12 2020-01-23 12.47 11.35 12.69 11.32 5716296 6.964347e+09 11.08 -8.25 -1.02 2.03 -36.791364 13 2020-02-28 10.22 10.85 11.39 10.22 8176614 8.916090e+09 10.31 -4.41 -0.50 2.91 -32.755988 14 2020-03-31 10.95 10.15 11.32 9.82 8748286 9.265608e+09 13.82 -6.45 -0.70 3.11 -40.461173 15 2020-04-30 10.11 10.63 10.79 9.98 4444344 4.553876e+09 7.98 4.73 0.48 1.58 57.243722 16 2020-05-29 10.44 10.57 10.57 10.13 3801628 3.948919e+09 4.14 -0.56 -0.06 1.35 -16.287209 17 2020-06-30 10.63 10.58 10.87 10.35 4611493 4.880872e+09 4.92 0.09 0.01 1.64 43.221173 18 2020-07-31 10.59 10.36 12.69 10.31 17903873 2.040465e+10 22.50 -2.08 -0.22 6.37 92.779477 19 2020-08-31 10.40 10.36 10.98 10.31 10579239 1.114334e+10 6.47 0.00 0.00 3.76 26.443089 20 2020-09-30 10.31 9.39 10.36 9.35 10758527 1.062955e+10 9.75 -9.36 -0.97 3.67 -28.505517 21 2020-10-30 9.44 9.26 9.93 9.25 8659783 8.302952e+09 7.24 -1.38 -0.13 2.95 13.887474 22 2020-11-30 9.28 10.06 10.53 9.22 15211953 1.477253e+10 14.15 8.64 0.80 5.18 51.617372 23 2020-12-31 10.08 9.68 10.39 9.44 10802366 1.063068e+10 9.44 -3.78 -0.38 3.68 44.363546 24 2021-01-29 9.64 9.96 10.23 9.52 13555010 1.336269e+10 7.33 2.89 0.28 4.62 18.379333 25 2021-02-26 9.94 10.54 11.12 9.90 18340719 1.945517e+10 12.25 5.82 0.58 6.25 11.180857 26 2021-03-31 10.59 10.99 11.24 10.36 17264511 1.866246e+10 8.35 4.27 0.45 5.88 -50.170857 27 2021-04-30 10.99 10.05 11.01 9.96 10330735 1.084681e+10 9.55 -8.55 -0.94 3.52 -11.142814 28 2021-05-31 9.97 10.27 10.43 9.88 8208193 8.330746e+09 5.47 2.19 0.22 2.80 40.989192 29 2021-06-30 10.23 10.00 10.38 9.96 8875254 8.996571e+09 4.09 -2.63 -0.27 3.02 -35.749590 30 2021-07-30 10.01 9.03 10.08 9.01 9368226 9.110368e+09 10.70 -9.70 -0.97 3.19 -91.401168 31 2021-08-31 9.03 9.05 9.39 8.92 7747928 7.090572e+09 5.20 0.22 0.02 2.64 -9.289064 32 2021-09-30 9.03 9.00 9.48 8.94 8386126 7.700020e+09 5.97 -0.55 -0.05 2.86 29.225518 33 2021-10-29 9.05 8.94 9.25 8.93 5146049 4.658420e+09 3.56 -0.67 -0.06 1.75 20.175154 34 2021-11-30 8.69 8.51 8.78 8.44 5998592 5.155727e+09 3.80 -4.81 -0.43 2.04 -26.740997 35 2021-12-31 8.53 8.53 8.81 8.51 6712135 5.783292e+09 3.53 0.24 0.02 2.29 31.048761
2 根据CAPM计算股票的历史期望收益率
计算期望收益率 E(ri)=rf+β(E(rm)−rf)
E(ri):股票i的预期收益率
rf: 无风险利率,
E(rm):市场指数收益率,即市场的预期平均收益率;
β: β系数,即资产标的系统性风险。
获取三年间每个月的无风险利率rf,选取当月末十年期国债收益率为准,若非交易日则另选一天:
#获取三年间每个月的无风险利率rf,选取当月末十年期国债收益率为准,若非交易日则另选一天
bond_china_yield_df1 = ak.bond_china_yield(start_date="20190101", end_date='20191231')
bond_china_yield_df2 = ak.bond_china_yield(start_date="20200101", end_date='20201231')
bond_china_yield_df3 = ak.bond_china_yield(start_date="20210101", end_date='20211231')
bond_china_yield_df = pd.concat([bond_china_yield_df1,bond_china_yield_df2,bond_china_yield_df3])
bond_china_yield_df = bond_china_yield_df[bond_china_yield_df['曲线名称']=='中债国债收益率曲线']
bond_china_yield_df = bond_china_yield_df.drop(['3月','6月','1年','3年','5年','7年','30年'],axis=1)
bond_china_yield_df['日期'] = bond_china_yield_df['日期'].astype(str)
#riqi = bond_china_yield_df['日期'].astype(str).str.split("-",n=1).str[-1]
#bond_china_yield_df['riqi'] = riqi
choosendays = pd.DataFrame(['2019-01-31','2019-02-28','2019-03-29','2019-04-30','2019-05-31','2019-06-28','2019-07-31','2019-08-29','2019-09-30','2019-10-31','2019-11-28','2019-12-31',
'2019-12-31','2020-02-28','2020-03-31','2020-04-30','2020-05-29','2020-06-30','2020-07-31','2020-08-31','2020-09-30','2020-10-29','2020-11-30','2020-12-31',
'2021-01-29','2021-02-26','2021-03-31','2021-04-30','2021-05-31','2021-06-30','2021-07-29','2021-08-31','2021-09-30','2021-10-29','2021-11-30','2021-12-31'],columns=['日期'])
#monthend = pd.DataFrame(['01-31','02-28','03-31','04-30','05-31','06-30','07-31','08-31','09-30','10-31','11-30','12-31'],columns=['riqi'])
bond_china_yield_df = pd.merge(bond_china_yield_df, choosendays, on = ['日期'], how = 'inner').sort_values(by=['日期'] ,axis=0,ascending=True)
rf_list_year = list(bond_china_yield_df['10年'])
rf_list = []
for r in rf_list_year:
rf_list.append(r/12)获取市场平均月收益率:
#获取市场平均月收益率
rm_list = list(ak.index_zh_a_hist(symbol='000016', period='monthly', start_date="20190101", end_date='20211231')['涨跌幅'])计算成分股的β(beta_list):
#计算成分股的β(beta_list)
beta_list,alpha_list,r_value_list,p_value_list,std_err_list = [],[],[],[],[]
codetoremove = []
for code in SH50_codes:
try:
beta,alpha,r_value,p_value,std_err=stats.linregress(rm_list,list(SH50_quotations_dic[code]['涨跌幅']))
beta_list.append(beta)
alpha_list.append(alpha)
r_value_list.append(r_value)
p_value_list.append(p_value)
std_err_list.append(std_err)
print(code,"计算完毕")
except:
print(code,"为中途新加入的成分")
codetoremove.append(code)
for code in codetoremove:
SH50_codes.remove(code)
print(code,"已从SH50_codes中移除")输出:
600000 计算完毕 600028 计算完毕 600030 计算完毕 600031 计算完毕 600036 计算完毕 600048 计算完毕 600050 计算完毕 600104 计算完毕 600196 计算完毕 600276 计算完毕 600309 计算完毕 600436 计算完毕 600438 计算完毕 600519 计算完毕 600547 计算完毕 600570 计算完毕 600585 计算完毕 600588 计算完毕 600690 计算完毕 600745 计算完毕 600809 计算完毕 600837 计算完毕 600887 计算完毕 600893 计算完毕 600900 计算完毕 601012 计算完毕 601066 计算完毕 601088 计算完毕 601138 计算完毕 601166 计算完毕 601211 计算完毕 601288 计算完毕 601318 计算完毕 601336 计算完毕 601398 计算完毕 601601 计算完毕 601628 计算完毕 601633 计算完毕 601668 计算完毕 601688 计算完毕 601728 为中途新加入的成分 601857 计算完毕 601888 计算完毕 601899 计算完毕 601919 计算完毕 601995 为中途新加入的成分 603259 计算完毕 603288 计算完毕 603501 计算完毕 603986 计算完毕 601728 已从SH50_codes中移除 601995 已从SH50_codes中移除
计算期望收益率 E(ri)=rf+β(E(rm)−rf):
#计算期望收益率 E(ri)=rf+β(E(rm)−rf)
def calEr(rf,beta,rm):
#已经将月度收益率转化为年化收益率
return 12 * (rf + beta * (rm - rf))
for code,beta in zip(SH50_codes,beta_list):
Er = []
for rf,rm in zip(rf_list,rm_list):
Er.append(calEr(rf,beta,rm))
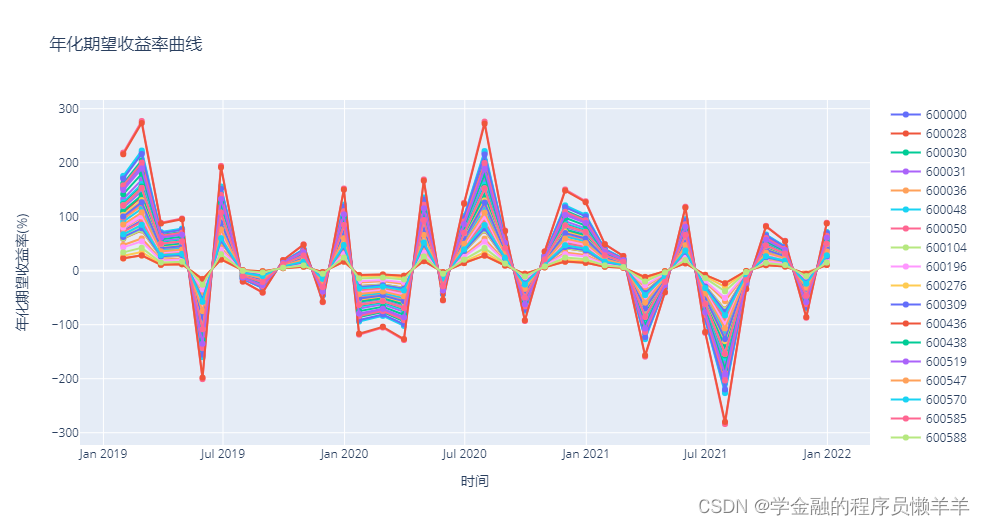
SH50_quotations_dic[code]['年化期望收益率'] = pd.DataFrame(Er)画历史预期收益率曲线图:
# 画收益率曲线图
lines = []
for code in SH50_codes:
lines.append(go.Scatter(y=SH50_quotations_dic[code]['年化期望收益率'], x=SH50_quotations_dic[code]['日期'],mode='lines+markers', name=code))
fig = go.Figure(lines)
fig.update_layout(
title = '年化期望收益率曲线', #定义生成的plot 的标题
xaxis_title = '时间', #定义x坐标名称
yaxis_title = '年化期望收益率(%)'#定义y坐标名称
)
fig.show() 输出:

3 计算收益率标准差(年化),夏普比率,相关系数
计算收益率标准差:
#计算收益率标准差
for code in SH50_codes:
returns = SH50_quotations_dic[code]['涨跌幅']
print(code,"年化收益率标准差为:",empyrical.annual_volatility(returns, period='monthly', alpha=2.0, annualization=True))600000 年化收益率标准差为: 5.406010081381646 600028 年化收益率标准差为: 5.3025414391860926 600030 年化收益率标准差为: 10.05529988976042 600031 年化收益率标准差为: 9.71219620676653 600036 年化收益率标准差为: 6.796814724326785 600048 年化收益率标准差为: 9.456735854187373 600050 年化收益率标准差为: 5.476258426079467 600104 年化收益率标准差为: 7.457042692266534 600196 年化收益率标准差为: 19.474689416192057 600276 年化收益率标准差为: 11.208026460660108 600309 年化收益率标准差为: 11.508608051615724 600436 年化收益率标准差为: 10.85135763578376 600438 年化收益率标准差为: 18.548525950075792 600519 年化收益率标准差为: 8.891268268845083 600547 年化收益率标准差为: 10.30548965665834 600570 年化收益率标准差为: 13.404746387540712 600585 年化收益率标准差为: 8.899909309329264 600588 年化收益率标准差为: 13.983813806377306 600690 年化收益率标准差为: 8.677304218019758 600745 年化收益率标准差为: 17.355014889806256 600809 年化收益率标准差为: 14.949436194709234 600837 年化收益率标准差为: 8.705648230379579 600887 年化收益率标准差为: 7.866874064053812 600893 年化收益率标准差为: 16.575248737629423 600900 年化收益率标准差为: 5.3488282354234835 601012 年化收益率标准差为: 14.575636521263828 601066 年化收益率标准差为: 17.833851029423858 601088 年化收益率标准差为: 8.235256662763298 601138 年化收益率标准差为: 9.627002842534054 601166 年化收益率标准差为: 7.3978005901368125 601211 年化收益率标准差为: 6.930288365241148 601288 年化收益率标准差为: 3.0379813029091207 601318 年化收益率标准差为: 7.677028629061413 601336 年化收益率标准差为: 8.590617805822482 601398 年化收益率标准差为: 4.239356270390776 601601 年化收益率标准差为: 9.380441468441512 601628 年化收益率标准差为: 11.104015014599199 601633 年化收益率标准差为: 19.2355834369205 601668 年化收益率标准差为: 4.611694313855206 601688 年化收益率标准差为: 9.182674935347213 601857 年化收益率标准差为: 7.23370060511523 601888 年化收益率标准差为: 18.286591809301154 601899 年化收益率标准差为: 13.813081064413671 601919 年化收益率标准差为: 17.790006582526868 603259 年化收益率标准差为: 13.300538940626094 603288 年化收益率标准差为: 11.388728749938798 603501 年化收益率标准差为: 15.104596357106374 603986 年化收益率标准差为: 19.998498316639548
计算夏普比率(简单认为无风险收益率为0.03):
#计算夏普比率(简单认为无风险收益率为0.03)
for code in SH50_codes:
returns = SH50_quotations_dic[code]['涨跌幅']
print(code,"过去三年的夏普比率为:",empyrical.sharpe_ratio(returns, risk_free=0.03, period='monthly', annualization=None))600000 过去三年的夏普比率为: -0.17461448941356442 600028 过去三年的夏普比率为: -0.2536945995877614 600030 过去三年的夏普比率为: 0.6300614624491767 600031 过去三年的夏普比率为: 1.1596904821171 600036 过去三年的夏普比率为: 1.0387264958792537 600048 过去三年的夏普比率为: 0.4344849511592825 600050 过去三年的夏普比率为: -0.4097629935731201 600104 过去三年的夏普比率为: -0.219882711171681 600196 过去三年的夏普比率为: 0.6256827603687464 600276 过去三年的夏普比率为: 0.14217371350402006 600309 过去三年的夏普比率为: 1.267464708647196 600436 过去三年的夏普比率为: 1.6330495092973676 600438 过去三年的夏普比率为: 1.1910027707620674 600519 过去三年的夏普比率为: 1.5077796378676218 600547 过去三年的夏普比率为: -0.27236789829745867 600570 过去三年的夏普比率为: 0.36050079676320834 600585 过去三年的夏普比率为: 0.4832925096162439 600588 过去三年的夏普比率为: 0.5825601235158362 600690 过去三年的夏普比率为: 0.9941538357301389 600745 过去三年的夏普比率为: 1.2908172558333204 600809 过去三年的夏普比率为: 1.692852256758357 600837 过去三年的夏普比率为: 0.4951821961868133 600887 过去三年的夏普比率为: 0.8485112775328982 600893 过去三年的夏普比率为: 0.8720209402558546 600900 过去三年的夏普比率为: 0.7142002160096603 601012 过去三年的夏普比率为: 1.299625049271544 601066 过去三年的夏普比率为: 0.906251740515804 601088 过去三年的夏普比率为: 0.38757562379349014 601138 过去三年的夏普比率为: 0.17681734092151608 601166 过去三年的夏普比率为: 0.4272881764382275 601211 过去三年的夏普比率为: 0.31518291928363057 601288 过去三年的夏普比率为: -0.6236612225283666 601318 过去三年的夏普比率为: -0.018801228218821013 601336 过去三年的夏普比率为: 0.03763596030626062 601398 过去三年的夏普比率为: -0.2542179599328554 601601 过去三年的夏普比率为: 0.09447664762768529 601628 过去三年的夏普比率为: 0.504955491946649 601633 过去三年的夏普比率为: 1.3859788042149317 601668 过去三年的夏普比率为: -0.2186698426985567 601688 过去三年的夏普比率为: 0.2312710354141348 601857 过去三年的夏普比率为: -0.4041246690427876 601888 过去三年的夏普比率为: 0.949695617331529 601899 过去三年的夏普比率为: 0.9629414241220862 601919 过去三年的夏普比率为: 1.133334805528026 603259 过去三年的夏普比率为: 0.5435409537143506 603288 过去三年的夏普比率为: 0.5355069452832935 603501 过去三年的夏普比率为: 1.7875848483960486 603986 过去三年的夏普比率为: 0.8448231017090055
计算相关系数并画:
#计算股票间的月收益率相关系数
#相关性分析
def my_cor_draw(data,my_method,sizex,sizey):
"""
data: dataframe数据类型
my_method: 检验方法,备选{‘pearson’, ‘kendall’, ‘spearman’}
"""
cor_data = data.corr(method=my_method)
#可视化
#print(cor_data)
import matplotlib.pyplot as mp,seaborn
names = []
for name ,dd in data.iteritems():
names.append(name)
seaborn.heatmap(cor_data, center=0, annot=True,xticklabels=names , yticklabels=names,cmap ='YlGnBu')
mp.rcParams['figure.figsize'] = (sizex, sizey) # 设置figure_size尺寸
mp.rcParams['font.sans-serif']=['SimHei']#黑体
# 设置刻度字体大小
mp.xticks(fontsize=12)
mp.yticks(fontsize=12,wrap = True)
# 设置坐标标签字体大小
ax = mp.gca()
ax.set_xlabel(..., fontsize=12)
ax.set_ylabel(..., fontsize=12,wrap = True)
# 设置图例字体大小
#ax.legend(..., fontsize=20)
mp.show()
return cor_data
data_all = pd.DataFrame()
for code in SH50_codes:
data_all[code] = pd.DataFrame(SH50_quotations_dic[code]['涨跌幅'])
cor_matrix1 = my_cor_draw(data_all,'pearson',35,30)输出:

4 以夏普比率、相关系数为条件筛选五只股票
条件:
挑选5只股票组成篮子,篮子股票必须满足下列三个条件: A)过去3年的夏普比率大于0.2; B)过去1年的夏普比率大于0.1; C)这5只股票彼此之间的相关系数之和最小。
#筛选满足条件1、2的股票
stockpool1 = []
for code in SH50_codes:
returns = SH50_quotations_dic[code]['涨跌幅']
if(empyrical.sharpe_ratio(returns, risk_free=0.03, period='monthly', annualization=None)>0.2):
stockpool1.append(code)
stockpool2 = []
for code in stockpool1:
returns = SH50_quotations_dic[code]['涨跌幅'][-12:-1]
if(empyrical.sharpe_ratio(returns, risk_free=0.03, period='monthly', annualization=None)>0.1):
stockpool2.append(code)
print("满足条件1、2的股票有:",stockpool2," 数量为",len(stockpool2))
#筛选满足条件3的股票
def get_subset(mylist,num):
result = []
n =len(mylist)
for i in combinations(mylist,num):
result.append(list(i))
return result
mincor = 1000
mingroup = []
for group in get_subset(stockpool2,5):
cor_matrix2_temp = data_all[group].corr(method='pearson')
corsum = (sum(sum(abs(cor_matrix2_temp.values)))-5)/2
if(corsum<mincor):
mincor = corsum
mingroup = group
print("最终组合为:",mingroup,"相关系数之和为:",mincor) 输出:
满足条件1、2的股票有: ['600036', '600196', '600309', '600436', '600438', '600745', '600893', '600900', '601088', '601633', '601899', '601919', '603259', '603501'] 数量为 14最终组合为: ['600436', '600745', '601088', '601633', '601899'] 相关系数之和为: 1.3162840831751845

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献3条内容
已为社区贡献3条内容





所有评论(0)