【视频】线性混合效应模型(LMM,Linear Mixed Models)和R语言实现案例
原文链接:http://tecdat.cn/?p=23050原文出处:拓端数据部落公众号如果您熟悉线性模型,意识到它们的局限,那么您应该学习线性混合模型mixed-model。本视频中,我们讨论了线性混合模型并在R软件中进行应用。视频:线性混合效应模型(LMM,Linear Mixed Models)和R语言实现线性混合效应模型(LMM,Linear Mixed Models)和R语言实现案例时长
最近我们被客户要求撰写关于线性混合效应模型的研究报告,包括一些图形和统计输出。
如果您熟悉线性模型,意识到它们的局限,那么您应该学习线性混合模型mixed-model。本视频中,我们讨论了线性混合模型并在R软件中进行应用。
视频:线性混合效应模型(LMM,Linear Mixed Models)和R语言实现
线性混合效应模型(LMM,Linear Mixed Models)和R语言实现案例
时长12:13
什么是混合效应建模,为什么要使用?
统计分析中许多问题的传统方法是拟合线性模型,通常使用最小二乘估计。与所有统计方法一样,最小二乘估计需要做出某些数学假设:数据符合正态分布的并且彼此独立。

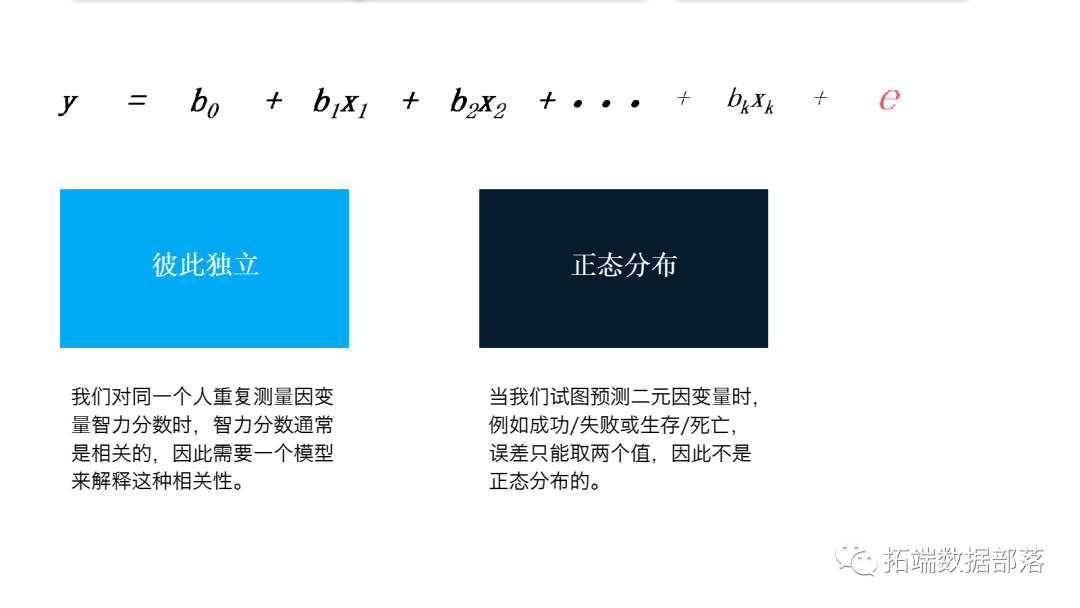
线性统计模型的一个常见示例是多元线性回归模型:

其中Y被称为因变量,X是自变量,β是要预测的未知参数,而ϵ是随机误差向量。
对于线性回归模型,我们需要假设误差是正态分布的并且彼此独立。自然,严重违反这些假设将导致统计模型几乎没有用处。
然而,在实际情况中,例如当我们对同一个人重复测量因变量智力分数时,智力分数通常是相关的,因此需要一个模型来解释这种相关性。
有时因变量显然不是正态分布的。当我们试图预测二元因变量时,例如成功/失败或生存/死亡,误差只能取两个值,因此不是正态分布的。但可能通过诸如泊松之类的分布很好地建模。逻辑回归和泊松回归分别是在这些情况下使用的模型,并且都是广义线性模型的特例。
这就是为什么要开发混合模型来处理如此混乱的数据,即使我们的样本量较小、结构化数据和许多协变量都可以拟合。
线性混合模型
处理相关数据的传统分析技术是重复测量方差分析和混合模型。相关数据的线性混合模型可以表述为(以回归模型格式):

其中 x变量代表固定效应,而 z变量代表随机效应。

与通常拟合最小二乘的传统线性模型不同,线性混合模型要么拟合最大似然,要么拟合 REML,限制最大似然。REML 是最大似然的一种变体,通常在变异性估计中具有较小的偏差。
混合模型非常适合聚类数据、重复测量和层次模型。虽然基于经典 ANOVA 的方法可以很好地处理某些特殊情况(例如来自没有缺失数据的平衡设计的重复测量 ANOVA),但混合模型对于处理更复杂的情况至关重要,包括缺失数据、按不同时间段测量的个体等。
混合模型还可以帮助我们避免假重复的统计错误,这是统计推断中的误差来源,我们将数据视为独立的,而实际上并非如此。这导致我们夸大了样本的大小,从而夸大了自由度和p-值,这可能导致错误地得出实际不存在的统计显着性结论(即 I 类错误)。假重复通常发生在具有层次结构的观察性研究或具有不同空间和/或时间尺度的设计实验中。
随机效应和固定效应
噪声,在统计文献中被称为“随机效应”。指定这些来源决定了我们测量中的相关结构。
在最简单的线性模型中,我们认为可变性源于测量误差,因此与其他任何因素无关。但通常是不切实际的。
考虑工业过程控制中的一个问题:测试制造的瓶盖直径的变化。我们想研究时间的固定效应:之前与之后。瓶盖是由几台机器生产的。很明显,机器内部和机器之间的直径存在差异。考虑到来自许多机器的瓶盖样本,我们可以通过去除每台机器的平均值来实现测量的标准化。这意味着我们把机器当作固定效应,减去它们,并认为机器内部的变异性是唯一的变异源。减去机器效应后,就去掉了机器间变异性的信息。
另外,在推断时间固定效应时,我们可以将机器间的变异性视为另一个不确定性的来源。在这种情况下,就不会减去机器效应,而是在LMM框架中把它当作一个随机效应。

LMM的相关概念
-
LMM 涉及到很多基础概念,因此它有许多名称:
-
方差分量:因为如示例所示,方差有不止一个来源。
-
分层模型或多级分析:因为我们可以将抽样视为分层的——首先对类别进行抽样,然后对其因变量进行抽样。
-
重复测量:因为我们对每个样本进行多次测量。

广义线性混合模型GLMM
广义线性混合模型相对线性混合模型更加灵活性,即我们可以为因变量假设除正态分布之外的许多族。

广义线性混合模型的一般形式是

其中 s是固定效应的数量。r是随机效应的数量。βj是固定效应xij 的参数。bik是随机效应的参数,而zik是随机效应的水平。链接函数 g(μi)=η用来表示,这样 y=g(μi) . 因此,混合模型与广义线性混合模型的结合,形成广义线性混合模型。
GLMM的链接函数

广义线性混合模型与线性混合模型 之间的不同之处在于因变量可以来自除正态分布之外的不同分布。此外,不是直接对因变量建模,而是应用一些链接函数,例如对于二元结果,我们使用Logistic链接函数和Logistic的概率密度函数。这些是

对于计数结果,我们使用对数链接函数和poisson的概率质量函数,或PMF。请注意,我们称之为概率质量函数而不是概率密度函数,因为支持是离散的(即对于正整数)。这些是

通过为因变量选择适当分布族并与线性预测因子相联系,可以更准确地对具有计数或比例的因变量设计进行建模。随机效应不再被忽视,而是被估计出来,并且可以对新的数据进行推断。
R语言对数据进行线性混合效应模型的拟合与可视化
在本文中,我们将用R语言对数据进行线性混合效应模型的拟合,然后可视化你的结果。
线性混合效应模型是在有随机效应时使用的,随机效应发生在对随机抽样的单位进行多次测量时。来自同一自然组的测量结果本身并不是独立的随机样本。因此,这些单位或群体被假定为从一个群体的 "人口 "中随机抽取的。示例情况包括
-
当你划分并对各部分进行单独实验时(随机组)。
-
当你的抽样设计是嵌套的,如横断面内的四分仪;林地内的横断面;地区内的林地(横断面、林地和地区都是随机组)。
-
当你对相关个体进行测量时(家庭是随机组)。
-
当你重复测量受试者时(受试者是随机组)。
混合效应的线性模型在R命令lme4和lmerTest包中实现。另一个选择是使用nmle包中的lme方法。lme4中用于计算近似自由度的方法比nmle包中的方法更准确一些,特别是在样本量不大的时候。
测量斑块长度
这第一个数据集是从Griffith和Sheldon(2001年,《动物行为学》61:987-993)的一篇论文中提取的,他们在两年内对瑞典哥特兰岛上的30只雄性领头鶲的白色额斑进行了测量。该斑块在吸引配偶方面很重要,但其大小每年都有变化。我们在这里的目标是估计斑块长度(毫米)。
读取和检查数据
-
从文件中读取数据。
-
查看数据的前几行,看是否正确读取。
-
创建一个显示两年研究中每只飞鸟的测量对图。可以尝试制作点阵图。是否有证据表明不同年份之间存在着测量变异性?
构建线性混合效应模型
-
对数据进行线性混合效应模型,将单个鸟类视为随机组。注:对每只鸟的两次测量是在研究的连续年份进行的。为了简单起见,在模型中不包括年份。在R中把它转换成一个字符或因子,这样它就不会被当作一个数字变量。按照下面步骤(2)和(3)所述,用这个模型重新计算可重复性。重复性的解释如何改变?
-
从保存的lmer对象中提取参数估计值(系数)。检查随机效应的输出。随机变异的两个来源是什么?固定效应指的是什么?
-
在输出中,检查随机效应的标准差。应该有两个标准差:一个是"(截距)",一个是 "残差"。这是因为混合效应模型有两个随机变异的来源:鸟类内部重复测量的差异,以及鸟类之间额斑长度的真实差异。这两个来源中的哪一个对应于"(截距)",哪一个对应于 "残差"?
-
同时检查固定效应结果的输出。模型公式中唯一的固定效应是所有长度测量的平均值。它被称为"(截距)",但不要与随机效应的截距相混淆。固定效应输出给了你平均值的估计值和该估计值的标准误差。注意固定效应输出是如何提供均值估计值的,而随机效应输出则提供方差(或标准差)的估计值。
-
从拟合模型中提取方差分量,估计各年斑块长度的可重复性*。
-
解释上一步中获得的重复性测量结果。如果你得到的重复性小于1.0,那么个体内测量结果之间的变化来源是什么。仅是测量误差吗?
-
产生一个残差与拟合值的图。注意到有什么问题?似乎有一个轻微的正向趋势。这不是一个错误,而是最佳线性无偏预测器(BLUPs)"收缩 "的结果。
分析步骤
读取并检查数据。
head(fly)
# 点阵图
chart(patch ~ bird)
# 但显示成对数据的更好方法是用成对的交互图来显示
plot(res=patch, x = year)
# 优化版本
plot(y = patch, x = factor(year), theme_classic)
拟合一个线性混合效应模型。summary()的输出将显示两个随机变异的来源:单个鸟类之间的变异(鸟类截距),以及对同一鸟类进行的重复测量之间的变异(残差)。每个来源都有一个估计的方差和标准差。固定效应只是所有鸟类的平均值--另一个 "截距"。
# 1.混合效应模型
# 2. 参数估计
summary(z)
# 5. 方差分量
VarCorr(z)
# 可重复性
1.11504^2/(1.11504^2 + 0.59833^2)## \[1\] 0.7764342# 7.残差与拟合值的关系图
plot(z)
金鱼视觉
Cronly-Dillon和Muntz(1965; J. Exp. Biol 42: 481-493)用视运动反应来测量金鱼的色觉。在这里,我们将对数据进行拟合,包括测试的全部波长。5条鱼中的每一条都以随机的顺序在所有的波长下被测试。敏感度的值大表明鱼可以检测到低的光强度。视运动反应的一个重要特点是,鱼不习惯,在一个波长下的视觉敏感度的测量不太可能对后来在另一个波长下的测量产生影响。
读取和检查数据
-
读取文件中的数据,并查看前几行以确保读取正确。
-
使用交互图来比较不同光波长实验下的个体鱼的反应。
-
使用什么类型的实验设计?*这将决定在拟合数据时使用的线性混合模型。
构建线性混合效应模型
-
对数据拟合一个线性混合效应模型。可以用lmer()来实现。发现“畸形拟合”,“boundary (singular) fit: see ?isSingular
” -
绘制拟合(预测)值**。每条鱼的预测值和观察值之间的差异代表残差。
-
你在(1)中做了什么假设?创建一个残差与拟合值的图,以检查这些假设之一。
-
从保存的lmer对象中提取参数估计值。检查固定效应的结果。给出的系数与使用lm分析的分类变量的解释相同。
-
检查随机效应的输出。我们的混合效应模型中再次出现了两个随机误差的来源。它们是什么?其中哪个对应于输出中的"(截距)",哪个对应于 "残差"?注意,在这个数据集中,其中一个变化源的估计标准差非常小。这就是畸形拟合信息背后的原因。鱼类之间的方差不太可能真的为零,但是这个数据集非常小,由于抽样误差,可能会出现低方差估计。
-
生成基于模型的每个波长的平均敏感度的估计。
-
各个波长之间的差异是否显著?生成lmer对象的方差分析表。这里测试的是什么效应,随机效应还是固定效应?解释方差分析结果。
*这是一个 "按实验对象 "的重复测量设计,因为每条鱼在每个实验下被测量一次。它本质上与随机完全区块设计相同(把每条鱼看作是 "区块")。
*可视化是首选,因为数据和拟合值都被绘制出来。请注意鱼与鱼之间的预测值是多么的相似。这表明在这项研究中,个体鱼之间的估计差异非常小。
*一般来说,在方差分析表中只测试固定效应。使用测试随机效应中没有方差的无效假设是可能的。
分析步骤
读取并检查数据。
x <- read.csv("fish.csv",
stringsAsFactors = FALSE)
head(x)
拟合一个线性混合效应模型。
该模型假设所有拟合值的残差为正态分布,方差相等。该方法还假设个体鱼之间的随机截距为正态分布。该方法还假设组(鱼)的随机抽样,对同一鱼的测量之间没有影响。
# # 1. 拟合混合效应模型。## boundary (singular) fit: see ?isSingular
# 2. 这就为每条鱼分别绘制了拟合值。
vis(z)
# 3.测试假设
plot(z)
# 4. 提取参数估计值
summary(z)
# 6. 基于模型的平均敏感度估计
means(z)
# 7. ANOVA方差分析
蓍草酚类物质的浓度
项目实验性地调查了国家公园的北方森林生态系统中施肥和食草的影响(Krebs, C.J., Boutin, S. & Boonstra, R., eds (2001a) Ecosystem dynamics of the Boreal Forest.Kluane项目. 牛津大学出版社,纽约)) ,目前的数据来自于一项关于植物资源和食草动物对底层植物物种防御性化学的影响的研究。
16个5x5米的小区中的每一个都被随机分配到四个实验之一。1)用栅栏围起来排除食草动物;2)用N-P-K肥料施肥;3)用栅栏和施肥;4)未实验的对照。然后,16块地中的每一块被分成两块。每块地的一侧(随机选择)在20年的研究中持续接受实验。每块地的另一半在头十年接受实验,之后让它恢复到未实验的状态。这里要分析的数据记录了欧蓍草(Achillea millefolium)中酚类物质的浓度(对植物防御化合物的粗略测量),欧蓍草是地块中常见的草本植物。测量单位是每克干重毫克丹宁酸当量。
可视化数据
-
从文件中读取数据。
-
检查前几行的数据。实验是作为一个有四个层次的单一变量给出的(而不是作为两个变量,围墙和肥料,用2x2因子设计的模型)。持续时间表示半块土地是否接受了整整20年的实验,或者是否在10年后停止实验。变量 "ch "是蓍草中酚类物质的浓度。
-
画一张图来说明不同实验和持续时间类别中蓍草中的酚类物质的浓度。在每个实验和持续时间水平的组合中没有很多数据点,所以按组画条形图可能比按组画箱形图更好。
-
添加线段来连接成对的点。
拟合一个线性混合效应模型
-
使用的是什么类型的实验设计?*这将决定对数据的线性混合模型的拟合。
-
在没有实验和持续时间之间的交互作用的情况下,对数据进行线性混合模型拟合。使用酚类物质的对数作为因变量,因为对数转换改善了数据与线性模型假设的拟合。
-
可视化模型对数据的拟合。按持续时间(如果xvar是实验)或实验(如果xvar是持续时间)分开面板。visreg()不会保留配对,但会允许你检查残差。
-
现在重复模型拟合,但这次包括实验和持续时间之间的相互作用。将模型与数据的拟合情况可视化。两个模型拟合之间最明显的区别是什么,一个有交互作用,另一个没有?描述包括交互项的模型 "允许 "什么,而没有交互项的模型则不允许。判断,哪个模型最适合数据?
-
使用诊断图检查包括交互项的模型的线性混合模型的一个关键假设。
-
使用拟合模型对象估计线性模型的参数(包括交互作用)。请注意,现在固定效应表中有许多系数。
-
在上一步的输出中,你会看到 "随机效应 "标签下的 "Std.Dev "的两个数量。解释一下这些数量指的是什么。
-
来估计所有固定效应组合的模型拟合平均值。
-
生成固定效应的方差分析表。哪些项在统计学上是显著的?
-
默认情况下,lmerTest将使用Type 3的平方和来测试模型项,而不是按顺序(Type 1)。用类型1来重复方差分析表。结果有什么不同吗?**
*实验采用了分块设计,即整个块被随机分配到不同的实验,然后将第二种实验(持续时间)的不同水平分配到块的一半。
*应该没有差别,因为设计是完全平衡的。
分析步骤
阅读并检查数据。
一个好的策略是对实验类别进行排序,把对照组放在前面。这将使线性模型的输出更加有用。
# 1. 读取数据
# 2. 检查
head(x)![]()
# 3. 分组带状图
# 首先,重新排列实验类别
factor(treat,levels=c("cont","exc","fer","bo"))
plot(data = x, y = log(phe), x = trea)
# 4. 在多个面板上分别绘制成对的数据
plot(data = x,y = log(ach, x = dur, fill = dur, col = dur)
拟合一个线性混合效应模型。固定效应是 "实验 "和 "持续时间",而 "块"是随机效应。拟合交互作用时,实验水平之间的差异大小在持续时间水平之间会有所不同。
由于随机效应也存在(块),系数表将显示两个随机变化来源的方差估计。一个是拟合模型的残差的方差。第二个是(随机)块截距之间的方差。
# 2. 拟合混合效应模型-无交互作用# 3. 可视化
vis(z)
# 4. 包括交互项和再次视觉化
vis(z.int, overlay = TRUE)
# 5. 绘制图表以检验方差齐性(以及正态性)
plot(z)
# 6. 系数
summary(z)
# 8. 模型拟合平均值
means(z, data = x)
# 9. 方差分析表
anova(z) # lmerTest中默认为3类平方和。
# 10. 改为1类
anova(z, type = 1)
![]()

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献16条内容
已为社区贡献16条内容





所有评论(0)