【算法】AOE网找关键活动、关键路径
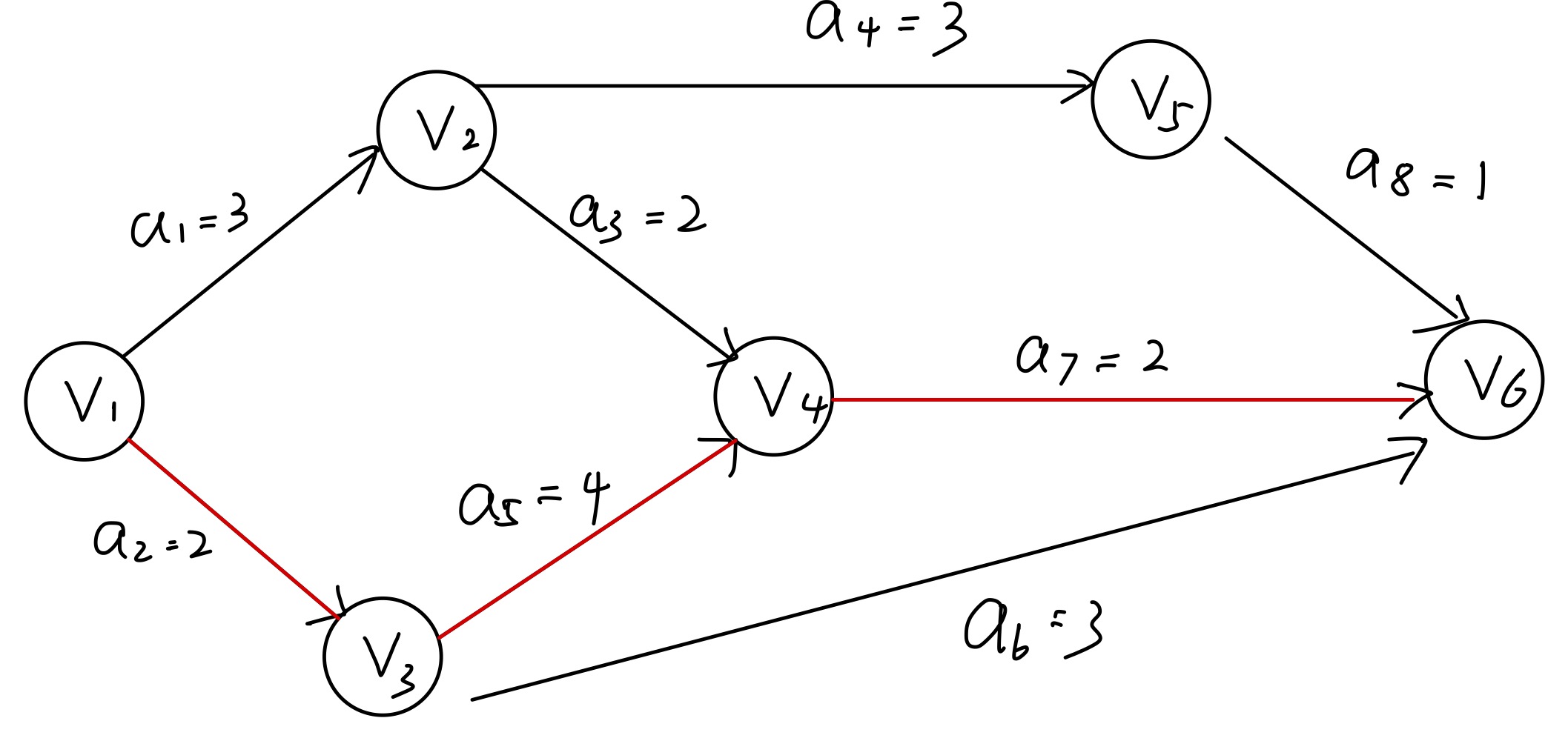
关键路径是什么?整个活动网影响整体耗时的路径。如果活动网没有任意一个分叉,所有节点连起来也为一条关键路径。找关键路径用于解决什么问题?项目推进中,如果要压缩工期,找到关键路径,并减小关键活动的耗时才能减少整体耗时,否则会做无用功。红色的边 = 关键活动。红色边 + 经过的节点 = 关键路径。存在关键路径的前提状态—— 图的顶点活动—— 图的边看本文需要具备的基础拓扑排序、逆拓扑排序参考王道教程,例
1. 前言
-
关键路径是什么?
整个活动网影响整体耗时的路径。如果活动网没有任意一个分叉,所有节点连起来也为一条关键路径。 -
找关键路径用于解决什么问题?
项目推进中,如果要压缩工期,找到关键路径,并减小关键活动的耗时才能减少整体耗时,否则会做无用功。如图示:- 红色的边 = 关键活动。
- 红色边 + 经过的节点 = 关键路径。

-
存在关键路径的前提
带正权的有向无环图,在业务中与数据结构的名词映射:
状态 —— 图的顶点
活动 —— 图的边 -
看本文需要具备的基础
拓扑排序、逆拓扑排序 -
参考
王道教程,例子来源于王道
2. 算法的名词解释
最早发生时间 ve 和 最迟发生时间 vl 都是描述的活动的开始时间。
我们讨论 活动 的 e 和 v 都是在描述这个活动在整个项目中两个属性,并且属性的值与边上的权相关其中:
ve都依赖于之前发生的状态,即当前讨论的v2活动作为箭头的终点,往前找活动
项目起点活动v1无前面的状态,也就无权,则ve(活动v1) = 0vl都依赖于之后发生的状态,即当前讨论的v2活动作为箭头的起点,往后找活动
项目终点活动v6无后面的状态,也就无权,但初始值来自于veve(活动v6) = vl(活动v6)
记忆点:先算完整个项目中状态的最早发生时间,才能算最迟发生时间。按拓扑排序依次计算状态的最早发生时间,按逆拓扑排序计算活动的最迟发生时间

2.1 状态最早发生时间 ve
明确一点,计算项目从开始节点往后推的时间。
引用王道的一个例子,厨师有两个帮手,帮手A负责洗番茄和切番茄,一共耗时4min。
ve(v1) = 0;
则 ve(v2) = ve(v1) + a2 = 1;

2.1.1 处在交叉处状态的 ve

帮手B打鸡蛋,一共耗时2min,要等待所有食材都处理完毕才“可以炒了”。所以 活动“可以炒了”的最早发生时间为4。
2.1.2 本例的所有ve
ve(v1) = 0;
ve(v3) = 0 + a2 = 2;
ve(v2) = 0 + a1 = 3;
ve(v4) = max { [ve(v2) + 连接v2的权] , [ve(v3) + 连接v3的权] } = 6; // 下文将讨论这个的计算依据
ve(v5) = ve(v4) + a4 = 6;
ve(v6) = max { [ve(v5) + 连接v5的权] , [ve(v4) + 连接v4的权] , [ve(v3) + 连接v3的权]} = 8;

2.1.3 求完ve,记得填入vl末项

2.2 求状态最迟发生时间 vl
参照2.1,推广得,最迟发生时间就是按逆拓扑序列进行计算。计算vl的前提是所有ve都被求出
2.2.1 处在交叉处状态的 vl
- 计算最迟发生时间,取最小差值。为什么?

根据上文求的值,已知最早4min的时候 “可以炒了” 必须发生,且已知在最早1min的时候 “可以切了” 必须发生。
- v1 -> v3 (一)
中间只需要完成耗时2min打鸡蛋,则对于v3而言,v1在4min - 2min = 2min时打鸡蛋就可以让V3按时发生 - v1 -> v2 (二)
中间只需要完成耗时1min洗番茄,则对于v2而言,v1在1min - 1min = 0min时洗番茄就可以让V2按时发生 - v2、v3都需要按时发生
取 (一) 和 (二) 的最小值,就能保证V2和V3都按时发生,这个值就是v1的最迟发生时间
上例V1的最迟发生时间为0
翻译过来就是,要同时保证V2和V3不延期,V1必须立刻马上开始
2.2.2 本例的所有vl

3. 求所有活动的 最早发生时间 e 和最迟发生时间 l
数据结构映射:
状态 —— 图的顶点
活动 —— 图的边
v1状态 ---> 活动a1 ---> v2状态
-
v1状态 ---> 活动a1
v1状态在活动a1的驱动下开始变化,也就是v1发生a1必然发生
一个活动必然在两个状态之间,则 v1的最早发生时间 即为活动a1的最早发生时间 -
活动a1 ---> v2状态
保证v2状态按时完成,则v2最迟发生时间 - a1耗时即是活动a1的最迟发生时间 -
综上
活动的最早发生,跟箭头开始的最早发生时间有关
活动的最迟发生,跟箭头终点的最迟发生时间有关

4. 找关键路径
时间余量:vl - ve == 0 的活动为关键活动,关键活动跟状态连起来就为关键路径。
v1 -a2-v3-a5-v4-a7-v6

5. 后记


开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献7条内容
已为社区贡献7条内容





所有评论(0)