概率基础——Metropolis-Hastings算法

Metropolis-Hastings算法是一种马尔科夫链蒙特卡洛（MCMC）方法，用于从复杂分布中抽样。它能够生成服从目标分布的样本序列，从而解决了在概率建模和贝叶斯推断等领域中遇到的抽样问题。本篇博客将介绍Metropolis-Hastings算法的理论基础以及Python实现，并通过例子解释其在实际问题中的应用。

Metropolis-Hastings算法的理论基础

Metropolis-Hastings算法是基于马尔可夫链的一种采样方法。它通过构建一个满足平稳分布的马尔可夫链，并使用接受-拒绝策略来生成服从目标分布的样本。该算法的关键在于设计一个转移核函数，使得转移后的样本能够以一定的概率接受，从而保证了马尔可夫链的收敛性。

Metropolis-Hastings算法的公式推导

假设我们要从目标分布$\pi (x)$中抽样，我们构建一个马尔可夫链，状态空间为$S$，转移核函数为$Q(x^{\prime }|x)$。我们的目标是设计一个接受概率$\alpha (x,x^{\prime })$，使得转移后的样本能够以一定的概率接受。

Metropolis-Hastings算法的转移规则：

1. 从当前状态$x_t$开始，根据转移核函数$Q(x^{\prime }|x_t)$抽取一个候选状态$x^{\prime }$。
2. 计算接受概率$\alpha (x_t,x^{\prime })$：
   $$\alpha (x_t,x^{\prime })=\min \left(1,\frac{\pi (x^{\prime })Q(x_t|x^{\prime })}{\pi (x_t)Q(x^{\prime }|x_t)}\right)$$
3. 以概率$\alpha (x_t,x^{\prime })$接受候选状态$x^{\prime }$，否则保持当前状态$x_t$。

Metropolis-Hastings算法的应用案例

贝叶斯推断

在贝叶斯统计中，Metropolis-Hastings算法常用于从后验分布中抽样，从而进行参数估计、模型比较等任务。通过Metropolis-Hastings算法，我们可以得到后验分布的样本，进而进行贝叶斯推断。

Python实现

下面通过一个简单的例子，使用Python实现Metropolis-Hastings算法对一维高斯分布进行抽样，并绘制出样本分布图像。

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats

# 目标分布：一维高斯分布
def target_distribution(x):
    return stats.norm.pdf(x, loc=5, scale=1)

# 转移核函数：对称随机游走
def transition_kernel(x):
    return stats.norm.rvs(loc=x, scale=1)

# Metropolis-Hastings算法
def metropolis_hastings(target_dist, trans_kernel, n_samples):
    samples = []
    current_state = 0  # 初始状态
    for _ in range(n_samples):
        candidate_state = trans_kernel(current_state)  # 从转移核函数中抽取候选状态
        acceptance_prob = min(1, target_dist(candidate_state) / target_dist(current_state))  # 计算接受概率
        if np.random.rand() < acceptance_prob:  # 接受候选状态
            current_state = candidate_state
        samples.append(current_state)
    return samples

# 抽样
samples = metropolis_hastings(target_distribution, transition_kernel, n_samples=10000)

# 绘制样本分布图像
plt.figure(figsize=(10, 6))
x = np.linspace(0, 10, 1000)
plt.plot(x, target_distribution(x), label='Target Distribution', color='blue')
plt.hist(samples, bins=50, density=True, label='Sample Distribution', color='skyblue', alpha=0.7)
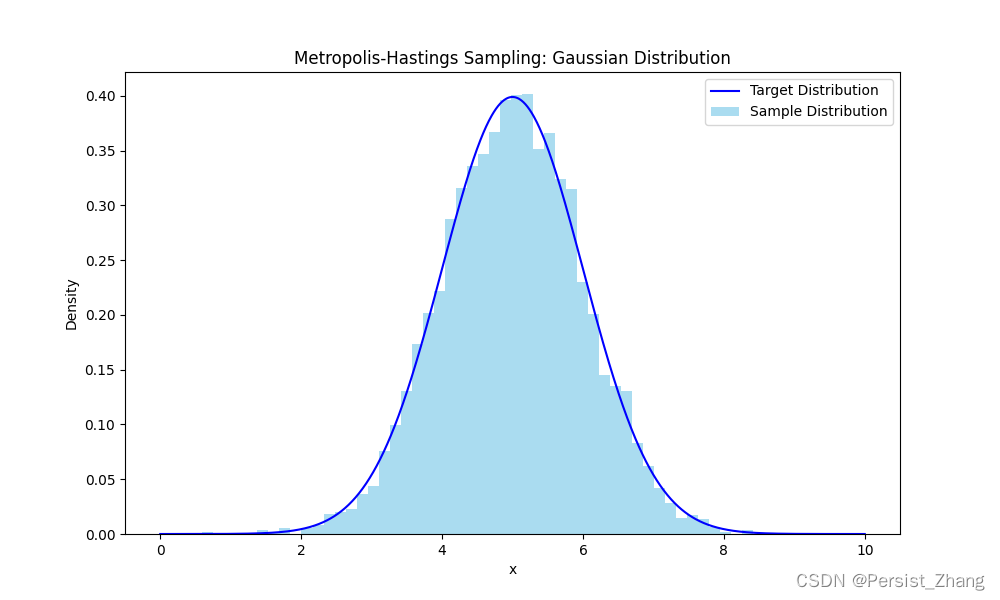
plt.title('Metropolis-Hastings Sampling: Gaussian Distribution')
plt.xlabel('x')
plt.ylabel('Density')
plt.legend()
plt.show()

上述代码实现了一个简单的Metropolis-Hastings算法，并绘制了样本分布图像。我们定义了目标分布为一维高斯分布，转移核函数为对称随机游走。然后，通过Metropolis-Hastings算法进行抽样，并绘制出样本分布图像。

结论

Metropolis-Hastings算法作为一种重要的抽样方法，在概率建模和贝叶斯推断等领域有着广泛的应用。通过本文的介绍，了解了Metropolis-Hastings算法的理论基础以及Python实现。希望本文对您理解Metropolis-Hastings算法有所帮助。