参考资料：
[1]李斌,朱浩文,邢鑫怡,et al.一种高性能多模式可配置SIMON加密电路设计[J].合肥工业大学学报（自然科学版）, 2022(006):045.
[2]Anand, R., Maitra, A. & Mukhopadhyay, S. Grover on SIMON[J]. Quantum Inf Process 19, 340 (2020).
[3]Feizi S , Ahmadi A , Nemati A .A hardware implementation of Simon cryptography algorithm[C]//2014 4th International Conference on Computer and Knowledge Engineering (ICCKE).0[2024-01-03].DOI:10.1109/ICCKE.2014.6993386.

0. 绪论

SIMON加密算法是一种轻量级的对称分组加密算法
主要包括轮函数运算和密钥调度两个部分。

注意辨析SIMON加密算法和量子算法领域解决Simon问题的Simon算法
本文将介绍SIMON加密算法的原理，有关Simon算法的介绍可以参看另一个量子算法专栏Quantum的介绍：（附链接）

• Simon算法
• Quantum专栏

1. 参数配置

1.1 参数介绍

根据所支持的分组长度和密钥长度不同，有10种不同的配置，记作：
$$SIMON2n/mn$$

其中：

• 2n：分组长度
• mn：密钥长度
• n：字长
• m：密钥字数

示例：SIMON 64/128模式：

1. 一个字的长度为32（n）
2. 密钥由4个字构成（m）

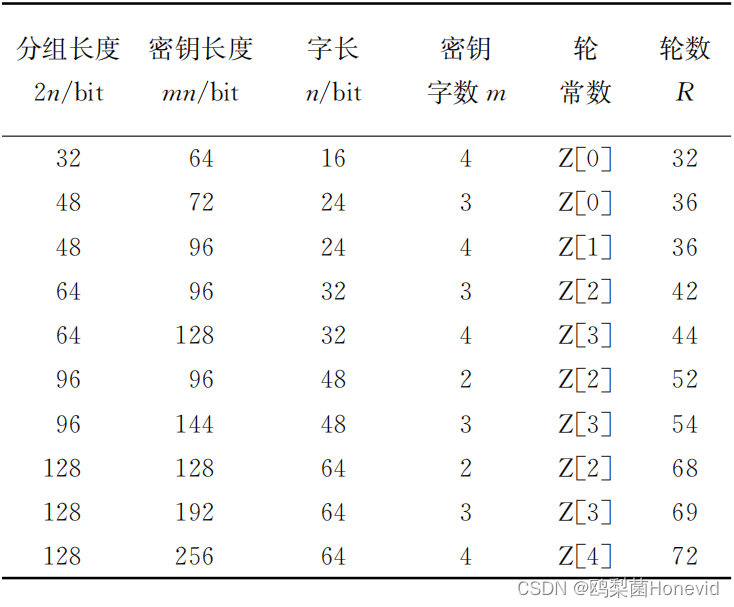
1.2 模式配置表

SIMON加密算法的分组长度、密钥长度以及必要的参数配置如下图：

其中：

• 轮常数：目的是消除循环移位带来的滑动特性
• 轮数：表示完成一次分组加密需要进行的迭代次数

2. 具体算法

2.1 Feistel结构特性

SIMON加密算法采用Feistel结构，主要由按位异或、按位与、非线性的循环移位构成。

Feistel结构是一种分组加密算法结构，有三个主要的特点：

1. 加密、解密过程一样
2. F函数只要固定输入有固定输出即可还原
3. 将分组密码的设计归为F函数的设计

2.2 轮函数运算

一次加密的流程：

1. 对2n位输入分组长度的数据分成高n位XL和低n位XR
2. XL循环左移1位和循环左移8位的数据进行按位与
3. 2中得到的数据和XR进行异或
4. XL循环左移2位，然后与3中得到的数据进行异或
5. 4中得到的数据与相应轮密钥进行异或
6. 5中得到的数据对原XL进行更新，原XL数据直接覆盖原XR数据

重复1-6的操作直至达到1.2表中规定的轮数R，即完成1次加密，相应的公式表达如下：

$$其中：x（或x_{i+1}）是高n位XL；y（或x_i）是低n位XR；$$
$$R_k是轮函数；S^{i}x表示x循环左移i位；k为密钥$$

过程示意图：

2.3 密钥调度

对特定的 SIMON 2n/mn，密钥调度的方法取决于 m 的取值，m 的 3 种取值对应的具体密钥调度方法有所区别。将输入初始密钥等分为m组，有：

当m=2或3 时

1. 对最高n 位循环右移3 位后与低 n 位进行异或得到中间值
2. 同时在循环右移3 位的基础上再右移 1 位与上述中间值再次异或
3. 最终异或上轮常数的第i位后再异或常量M，并更新密钥寄存器的最高 n 位
4. 各组密钥寄存器分别由上一组密钥寄存器的值进行覆盖更新。

相应的公式表达如下：

$$其中：x是高n位XL；y是低n位XR；R_k是轮函数；S^{i}x表示x循环左移i位；k为密钥$$

3 加密解密

3.1 加密

加密 $oracle$ 的输入是一个 2n-$bit$ 的明文块 $P$, 这个块被分成 n-$bit$ 的子块$P=$ $(L_0,R_0)$, 这是密码的初始状态。该加密方案由轮函数的$T$次应用和由密钥调度产生的轮密钥组成。得到的密文为 2n 位块$C=(L_{T-1},R_{T-1})$。

3.2 解密

对密文$C=(L_{T-1},R_{T-1})$进行解密，首先将分组密码的 L 和 R 部分交换，即解密$oracle$ 的输入为$(R_{T-1},L_{T-1})$。然后，以相反的轮密钥次序(即轮密钥$k_{T-1},\dots ,k_0$)运行 T 次轮函数运算，最后交换两个子块。