粒子群优化算法 (PSO)

粒子群优化算法（Particle Swarm Optimization, PSO）是一种基于群体智能的优化算法，最早由Kennedy和Eberhart在1995年提出。它模仿了鸟群觅食的行为，通过群体协作和信息共享，在搜索空间中寻找最优解。本文将详细介绍PSO算法的原理、提供Python代码示例和可视化结果。

算法原理

PSO算法的核心思想是通过一群“粒子”在搜索空间中的相互协作，逐步逼近最优解。每个粒子代表一个可能的解，它具有位置和速度两个属性。粒子的位置表示一个候选解，速度则决定了粒子在下一步的位置变化。

算法的运行过程如下：

1. 初始化：在搜索空间内随机生成一群粒子，初始化它们的位置和速度。
2. 评价适应度：根据目标函数计算每个粒子的适应度值。
3. 更新粒子位置和速度：
   • 每个粒子记住自己历史上最佳的位置（个体最佳位置，$p_{best}$）。
   • 整个粒子群记住历史上最佳的位置（全局最佳位置，$g_{best}$）。
   • 根据个体最佳位置和全局最佳位置，更新每个粒子的速度和位置。
4. 迭代：重复评价和更新步骤，直到达到停止条件（如达到最大迭代次数或适应度满足某个阈值）。

算法公式

粒子的位置和速度更新公式如下：

$$v_i(t+1)=w\cdot v_i(t)+c_1\cdot r_1\cdot (p_{bes{t}_i}-x_i(t))+c_2\cdot r_2\cdot (g_{best}-x_i(t))$$

$$x_i(t+1)=x_i(t)+v_i(t+1)$$

其中：

• $v_i(t)$ 是粒子$i$ 在第 $t$ 次迭代时的速度。
• $x_i(t)$ 是粒子$i$在第$t$ 次迭代时的位置。
• $w$ 是惯性权重，控制速度的延续性。
• $c_1$和 $c_2$是加速常数，通常取值为2。
• $r_1$和 $r_2$是介于0和1之间的随机数。
• $p_{bes{t}_i}$是粒子 $i$ 的历史最佳位置。
• $g_{best}$ 是全体粒子的历史最佳位置。

算法代码

一个简单的PSO算法的Python实现示例：

import numpy as np
import matplotlib.pyplot as plt
import imageio

class Particle:
    def __init__(self, num_dimensions):
        self.position = np.random.uniform(-10, 10, num_dimensions)
        self.velocity = np.random.uniform(-1, 1, num_dimensions)
        self.best_position = self.position.copy()
        self.best_score = float('inf')

class PSO:
    def __init__(self, objective_function, num_particles, num_dimensions, num_iterations, w=0.5, c1=1.5, c2=1.5):
        self.objective_function = objective_function
        self.num_particles = num_particles
        self.num_dimensions = num_dimensions
        self.num_iterations = num_iterations
        self.w = w
        self.c1 = c1
        self.c2 = c2
        self.particles = [Particle(num_dimensions) for _ in range(num_particles)]
        self.g_best_position = np.random.uniform(-10, 10, num_dimensions)
        self.g_best_score = float('inf')
        self.frames = []

    def optimize(self):
        for iteration in range(self.num_iterations):
            for particle in self.particles:
                fitness = self.objective_function(particle.position)
                if fitness < particle.best_score:
                    particle.best_position = particle.position.copy()
                    particle.best_score = fitness
                if fitness < self.g_best_score:
                    self.g_best_position = particle.position.copy()
                    self.g_best_score = fitness

            for particle in self.particles:
                inertia = self.w * particle.velocity
                cognitive = self.c1 * np.random.random() * (particle.best_position - particle.position)
                social = self.c2 * np.random.random() * (self.g_best_position - particle.position)
                particle.velocity = inertia + cognitive + social
                particle.position += particle.velocity

            self.plot_particles(iteration)

        self.save_gif()
        return self.g_best_position, self.g_best_score

    def plot_particles(self, iteration):
        plt.clf()
        positions = np.array([p.position for p in self.particles])
        plt.scatter(positions[:, 0], positions[:, 1], color='blue', label='Particles')
        plt.scatter(self.g_best_position[0], self.g_best_position[1], color='red', marker='*', s=200, label='Global Best')
        plt.xlim(-10, 10)
        plt.ylim(-10, 10)
        plt.title(f'Iteration {iteration + 1}')
        plt.legend()
        plt.savefig(f'frame_{iteration}.png')
        self.frames.append(f'frame_{iteration}.png')

    def save_gif(self):
        images = []
        for filename in self.frames:
            images.append(imageio.imread(filename))
        imageio.mimsave('pso_optimization.gif', images, duration=0.2)

def objective_function(x):
    return np.sum(x**2)

# PSO参数
num_particles = 30
num_dimensions = 2
num_iterations = 100

pso = PSO(objective_function, num_particles, num_dimensions, num_iterations)
optimal_position, optimal_value = pso.optimize()

plt.show()
print(f'Optimal Solution: {optimal_position}')
print(f'Objective Value: {optimal_value}')

代码解释

1. 保存图像帧：

   • 在plot_particles方法中，每次绘制后调用plt.savefig保存当前图像为PNG文件，并将文件名保存到self.frames列表中。

2. 生成GIF：

   • 在save_gif方法中，使用imageio.imread读取每个保存的PNG文件，并使用imageio.mimsave将这些帧合成为GIF图像。

3. 主程序：

   • 创建PSO对象并调用optimize方法进行优化。
   • 优化过程结束后，GIF图像将保存在当前目录下，文件名为pso_optimization.gif。

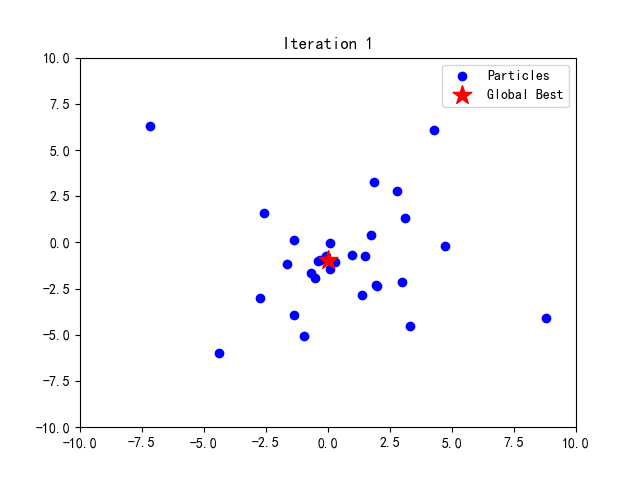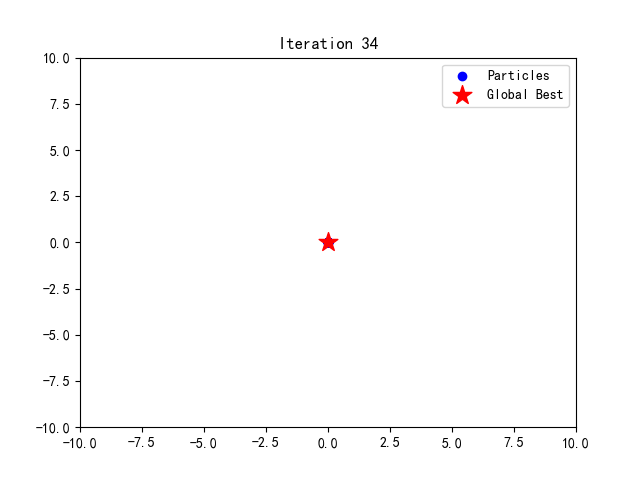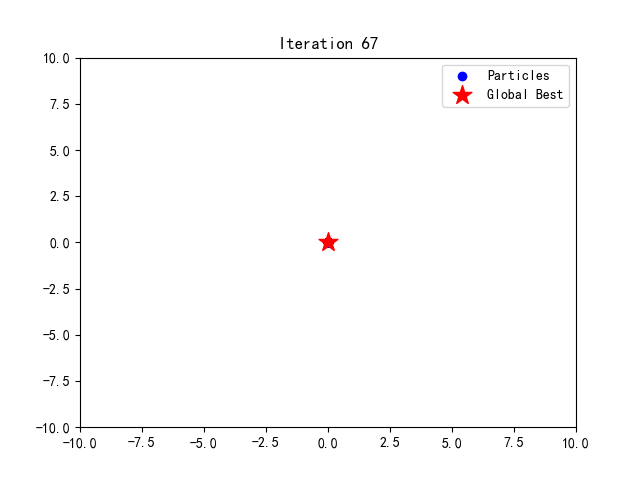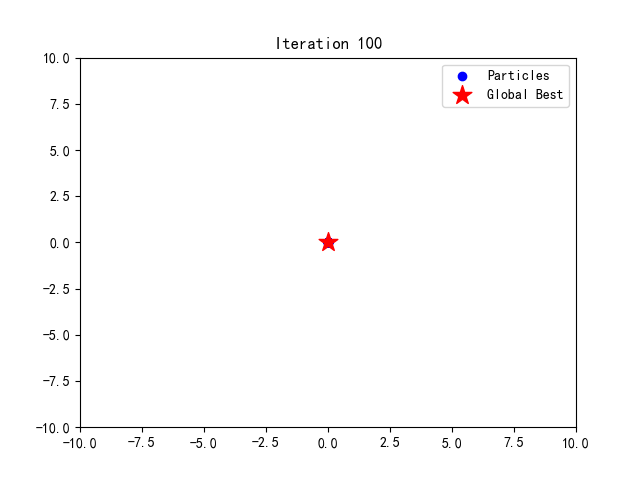
运行此代码后，可以在当前目录下找到生成的GIF文件，展示PSO优化过程的动态变化。

结论

PSO算法是一种简单而有效的优化算法，适用于各种复杂的优化问题。通过模拟自然界的群体行为，PSO能够快速逼近全局最优解。其优点包括易于实现、参数设置简单以及良好的全局搜索能力。然而，PSO也存在收敛速度较慢、易陷入局部最优等问题。通过调整算法参数和引入改进策略，可以进一步提升PSO的性能。