算法与数据结构——并查集、种类并查集和带权并查集
并查集是一种树型的数据结构,用于处理一些不相交集合的合并及查询问题。并查集的思想是用一个数组表示了整片森林(parent),树的根节点唯一标识了一个集合,我们只要找到了某个元素的的树根,就能确定它在哪个集合里。
并查集
什么是并查集?
并查集是一种树型的数据结构,用于处理一些不相交集合的合并及查询问题。
并查集的思想是用一个数组表示了整片森林(parent),树的根节点唯一标识了一个集合,我们只要找到了某个元素的的树根,就能确定它在哪个集合里。
并查集的用途
并查集支持以下两种操作:
合并(Union):把两个不相交的集合合并为一个集合。
查询(Find):查询两个元素是否在同一个集合中。
其主要作用包括以下几个方面:
1、判断两个不同元素是否在同一个集合(连通块)中
2、求某元素所在集合(连通块)的元素个数
3、求连通分支数(如果一个图中所有点都存在可达关系(直接或间接相连),则此图的连通分支数为1;如果此图有两大子图各自全部可达,则此图的连通分支数为2……。
如何实现?
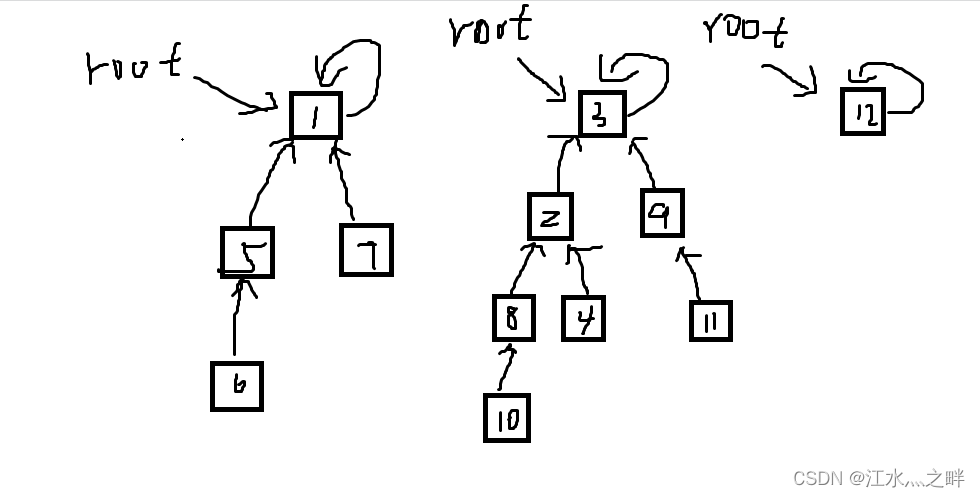
并查集的重要思想在于,用集合中的一个元素代表集合。如下图所示,代表这个集合的节点叫作根节点(root),集合中其他的元素是根节点的子孙。在同一个集合的元素,都能找到相同的根节点来代表他们自己所在的集合,而只有指向**父节点(parent)**指向自己的才能成为根节点(root)。

并查集初始化
考虑以下情形,假设现有n个元素,编号分别为1,2,3…n(编号代表各元素互不相同)。
初始化时,我们给每个元素分配一个唯一标识parent,并且如果两个元素的根节点相同,则他们属于同一个集合。在该定义下,初始化直接令每个元素的parent等于自身编号即可,如图所示,可以看出此时每个节点都是其所在集合的根节点(即p[x]=x),因此,此时每个元素都单独属于一个集合,。

代码如下:
for(int i=1;i<=n;i++) p[i]=i;
并查集的查询操作
从刚刚的介绍来看,我们在查询某个元素位于哪个集合时,只需查询到该元素对应的parent标识即可,即找到该元素所在集合的根节点(parent节点)即可。给定元素 x,我们可以使用如下代码来查询该元素所属集合:
查询,非压缩路径法
//查询编号为x的节点属于哪个集合(非压缩路径,每次查询需要从树底部向上查询到根节点)
int find(int x) {
//如果x不是根节点,就沿着x向上找到x的父节点
//递归判断父节点是否为根节点
if (p[x] != x) return find(p[x]);
//是根节点,返回集合编号
else return x;
}
查询,压缩路径法
//只要执行一次查询,路径上的所有节点的parent都会直接变为根节点(即集合号)
int find_compress_path(int x) {
if (p[x] != x)
p[x] = find_compress_path(p[x]);
else
return p[x];
}
特殊地,初始化时每个元素各自形成成一个集合,此时查询到所在集合就是他们各自的编号值。但是此时,看代码可能还会存在疑问,为什么要使得p[x]==x时,此时找到的x才是所在集合号数呢?看了下面的合并操作,在会过来看查询代码,我们就能慢慢理解了。
并查集的合并操作
根据上述介绍,可知初始化时,每个节点各自是一个集合,那么集合是如何合并的呢?接下来看以下流程:
1、初始化状态,所有节点各自为营,每个节点有自己的阵营(即每个节点都自成一个集合,每个节点的parent节点就是自己,即p[x]=x)

2、但是随着某种条件的进行,1和3由于某种条件(可能是题目中的题意),导致3号要加入1号的阵营,从而1号和3号此时同属为一个集合,此时3号需要合并到1号的集合中去,该怎么做呢?此时自然是改变原有的p[3]=3,令p[3]=1,使得3号指向1,从此3号的parent指向1号节点。当寻找三号所在的集合时,我们就会一值往上寻找3号所在树的根节点(即p[x]=x的节点)来作为集合的代表。

3、随着某种条件的进行,1和2由于某种条件(可能是题目中的题意),导致2号要加入1号的阵营。此时,改变p[2]=2为p[2]=1,使得2号的父节点变为1号节点,从而2号加入到1号的阵营,从此1、2、3号都有了共同的根节点即1号,因此也就使得1、2、3号同属于一个集合了。

4、随着某种条件的进行,与上述描述的情况相同,4、5、6号节点也由于某种条件的促使,使得他们需要成为同一阵营,此时改变p[6]=6,p[5]=5为p[6]=4,p[5]=4,使得5号和6号的父节点指向4号,从此4、5、6号节点有了共同的根节点即4号,因此4、5、6号属于同一个集合。

5、最后,由于某种条件的进行,发现4号阵营中的某个节点其实与1号的阵营某个节点应该同属于一个集合,然而4号阵营的所有元素又都同属于一个集合,因此,此时就需要将1集合和4集合中所有元素都合并到同一个集合。那此时该如何做呢?我们以4号阵营中5号节点,由于某种条件的促使下,应该与1号阵营的2号节点属于同一个集合为例。此时我们就需要找到代表5号所在集合根节点(root)即4号和代表2号所在集合的根节点(root)即1号,然后将4号根节点的父节点指向1号根节点,即将p[4]=4改变为p[4]=1,从此使得4阵营所有节点加入到1阵营中,此时,1,2,3,4,5,6所有节点都同属于一个集合即1号集合。

并查集合并操作的代码实现如下:
//合并(a,b)所在的集合,【按秩合并更优,但效果不明显】
void merge(int a,int b) {
int aSet = find_compress_path(a);
int bSet = find_compress_path(b);
//如果不是同一个,则属于不同集合,需要合并
if (aSet != bSet)
p[bSet] = aSet;//只需将b集合的根节点设置一个parent指针,并且指向b集合的根节点,就可以将b集合合并的a结合当中
}
注意此处需要借用上文查询操作中已经实现的查询代码,因为,当我们执行合并操作的时候,我们首先需要做的就是找到需要合并的元素所在的集合,即需要找到p[x]=x的节点,再执行合并操作,将父节点的指针重新下指向新集合。
查询操作的压缩路径补充
由于每次查询x操作,都需要递归从x元素开始找,再找到x的父节点,一层一层往上查找,直到查找到所在集合的根节点,才能得出x所在的集合。然而并查集的树高往往就是查询时间复杂度的关键所在,而压缩查询的路径能够降低树高从而大大降低查询的时间复杂度。
如下图所示,当我们执行查询8号节点所在的集合时,一旦执行一次查询操作,压缩路径代码将会使得并查集树从图中左侧形状变为图中右侧形状。虽然改变了路径和形状,但是此时并查集树并不会破坏其原有性质,仍然可以通过某个元素x直接查询到x所在的集合(类似于每个节点都是单独一个一个插入进并查集树的状态)。

并查集应用题
AC代码如下:
#include<iostream>
using namespace std;
const int N = 100010;
//定义:初始化为多个集合
int p[N];
//查询编号为x的节点属于哪个集合(非压缩路径,每次查询需要从树底部向上查询到根节点)
int find(int x) {
//如果x不是根节点,就沿着x向上找到x的父节点
//递归判断父节点是否为根节点
if (p[x] != x) return find(p[x]);
//是根节点,返回集合编号
else return x;
}
//查询,压缩路径法
//只要执行一次查询,路径上的所有节点的parent都会直接变为根节点(即集合号)
int find_compress_path(int x) {
if (p[x] != x)
p[x] = find_compress_path(p[x]);
else
return p[x];
}
//合并(a,b)所在的集合,【按秩合并更优,但效果不明显】
void merge(int a,int b) {
int aSet = find_compress_path(a);
int bSet = find_compress_path(b);
//如果不是同一个,则属于不同集合,需要合并
if (aSet != bSet)
p[bSet] = aSet;//只需将b集合的根节点设置一个parent指针,并且指向b集合的根节点,就可以将b集合合并的a结合当中
}
int main() {
int n, m;
ios::sync_with_stdio(NULL);
cin.tie(nullptr);
cin >> n >> m;
//初始化,每个节点都是一个集合,自己就是根节点
for (int i = 1; i <= n; i++) p[i] = i;
while (m--) {
char op;
cin >> op;
int a, b;
cin >> a >> b;
if (op == 'M') merge(a, b);
else
{
if (find_compress_path(a) == find_compress_path(b)) cout << "Yes"<< '\n';
else
cout << "No"<< '\n';
}
}
return 0;
}
AC代码:
#include<iostream>
using namespace std;
const int N = 100010;
int p[N];//集合集
int sz[N];//记录集合(联通块)中的节点个数
int find(int x) {
if (p[x] != x)
p[x] = find(p[x]);
return p[x];
}
void merge(int a, int b) {
int aSet = find(a);
int bSet = find(b);
if (aSet != bSet) {
p[bSet] = aSet;
//合并之后需要将两个连通块集合的个数相加起来
sz[aSet] += sz[bSet];
}
}
int main(){
ios::sync_with_stdio(NULL);
cin.tie(nullptr);
int m, n;
cin >> n >> m;
//初始化联通块集合
for (int i = 1; i <= n; i++) {
p[i] = i;
sz[i] = 1;//记录连通块集合的个数
}
while (m--) {
string op;
int a, b;
cin >> op;
if (op == "C") {
cin >> a >> b;
merge(a, b);
}
else if (op == "Q1") {
cin >> a >> b;
if (find(a) == find(b))
cout << "Yes" << '\n';
else
cout << "No" << '\n';
}
else
{
cin >> a;
cout << sz[find(a)] << endl;
}
}
return 0;
}
种类并查集
种类并查集的概念
种类并查集(Type Union-Find)是并查集的一个变种,它通过扩大原有的并查集空间来维护多种不同的关系。在处理某些问题时,比如需要区分元素之间的“朋友”和“敌人”关系,仅使用普通的并查集是不够的,因为它只能维护元素之间的一种关系。
为了解决这个问题,种类并查集将每个元素的表示扩大到n倍。这样做的目的是为了能够同时维护“朋友”关系和“敌人”关系。具体来说,如果有n个元素,我们会创建一个2n大小的数组,其中前n个位置用来表示元素之间的“朋友”关系,而后n个位置用来表示“敌人”关系。
种类并查集和普通并查集解决问题差异
1、普通并查集,维护的是具有连通性、传递性的关系,例如亲戚的亲戚是亲戚,即a和b是亲戚,则c只要和a、b其中一个是亲戚,则a,b,c都是亲戚,都同属一个集合。
2、但有时候,我们却需要用到种类并查集来维护另一种关系:敌人的敌人是朋友,即a和b是敌人,c和a是敌人,但c却未必并不b有仇从而也为敌人,相反有可能c和b是朋友;同时a和b是朋友,c和a是朋友,但是c却未比能和b成为朋友。
何时使用种类并查集
当我们不能清楚的知道具体哪些元素应该为一类,我们只能只知道哪些元素不能为一类,此时一般并查集就没法处理这种问题了,就需要用到种类并查集。
种类并查集的实现
此处,以敌人的敌人是朋友的关系为例子,对种类并查集的实现进行说明。
1、种类并查集初始化
此处需要维护敌人和朋友两种关系,因此需要初始化两倍大小的并查集。其中令1 ~ n为朋友关系,而n+1 ~ 2n为敌人关系。即对于任意一个i∈[1,n],他的敌人都是i+n,这个敌人并不是真实存在的,只是假想出来的,为了分类使用。比如我们现在有4个人:

2、合并操作
我们现在知道1和2是敌人关系,所以自然就可以推出的2应该和1的敌人1+n是朋友关系,1应该和2的敌人2+n是朋友关系,图中表示为1和6是朋友关系,2和5是朋友关系,故合并1和6以及合并2和5。

此时我们又知道2和4是敌人关系,故可以得到下图。2和4是敌人关系,则可以推出,4和2的敌人2+n是朋友关系;2和4的敌人4+n是朋友关系。图中表示为2和8是朋友关系,4和6是朋友关系。故合并2和8以及4和6.

此处合并操作与普通并查集合并操作并无不同。
注意:需要注意合并的方向,有时合并的方向会影响题目的结果,最好是一次合并实点到虚点、一次合并虚点到实点。
种类并查集的应用
AcWing 240. 食物链
由于该题是A吃B,B吃C,C吃A的循环,此时需要维护三类关系来维护自身同类,被捕食、被捕食
三类,因此需要开3倍的并查集空间,即3n的种类并查集
 AC代码如下:
AC代码如下:
#include<iostream>
using namespace std;
const int N = 300010;
int p[N];
//查询
int find(int x) {
if (p[x] != x)
p[x] = find(p[x]);
return p[x];
}
//合并集合
void merge(int a, int b) {
int aSet = find(a);
int bSet = find(b);
if(aSet!=bSet)
p[bSet] = aSet;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, k;
cin >> n >> k;
//并查集初始化
for (int i = 1; i <= 3 * n; i++) p[i] = i;
//记录假话的数量
int res=0;
while (k--) {
int op, x, y;
cin >> op >> x >> y;
if (x > n || y > n) {
res++;
continue;
}
//说的话是 x和y是同类
else if (op == 1) {
//如果x和y是捕食关系或被捕时关系,则该句话是假话
if (find(x + n) == find(y) || find(x + 2 * n) == find(y)) {
res++;
continue;
}
// 如果上述情况不成立,那说明是真话,则x和y是同类
merge(x, y); //则x和y是一族
merge(x + n, y + n); //x的猎物和y的猎物是一族
merge(x + 2 * n, y + 2 * n); //x的天敌和y的天敌是一族
}
//说的话是 x吃y
else if(op==2)
{
//如过x和y是同类或x和y是被捕时关系时,则该句话时假话
if (find(x) == find(y) || find(x + 2 * n) == find(y)) {
res++;
continue;
}
// 如果上述情况不成立,那说明是真话,则x和y是捕食关系
merge(x + n, y);//x+n和y是一族
merge(x + 2 * n, y + n);//x + 2 * n和y+n是一族
merge(x, y + 2 * n);//x和y+2*n是一族
}
}
cout << res << '\n';
return 0;
}
种类并查集扩大区间的重点注意之处
上面提到种类并查集中,当需要维护k类关系时,就需要将并查集扩大k倍来维护这些关系,即生成kn个区间。
即
1——k,k+1——2k,…(n-1)k+1——n*k的区间,其中每个区间的固有的关系其实不是真实存在的,只是假想出来的,为了分类使用的,最终关系还是得看形成的并查集后,两个元素的根节点是否相同。
以食物链题目为例,简单来说就是,分成的3个区间,一开始只是为了存放两个元素(x,y)之间的对应关系(因为利用种类并查集的题目,都只能得知两者的对应关系)的,最终需要通过合并操作才能得某个元素是类别A还是类别B还是类别C。举个例子来说,x和y两者是捕食关系,但是我们并不知道x和y具体是A类和B类,还是B类和C类,还是C类和A类之间的关系。因此,我们此处就要用到这层对应关系放到假想出来的3个区间当中,x和y两者是捕食关系,所以指定一个点为中心,以x为中心,则将x放到与自己同类的1——n的区间,y则放到以x为中心的n+1——2*n的区间,然后等待合并。
带权并查集
普通的并查集仅仅记录的是集合的关系,这个关系无非是同属一个集合或者是不在一个集合。
带权并查集不仅记录集合的关系,还记录着集合内元素的关系或者说是集合内元素连接线的权值。
带权并查集的实现
带权并查集的实现,需要在普通并查集的基础上,注意以下问题:
1、每个节点都记录的是与根节点之间的权值,那么在Find的路径压缩过程中,权值也应该做相应的更新,因为在路径压缩之前,每个节点都是与其父节点链接着,那个Value自然也是与其父节点之间的权值。
2、在两个并查集做合并的时候,权值也要做相应的更新,因为两个并查集的根节点不同。
还是以 AcWing 240. 食物链 为例子来说明。
如图所示,食物链形成一个循环,通过带权并查集,用某个节点到根节点的路径长度来区别不同的关系。虽然我们无法知道图中根节点1号,具体是A类还是B类还是C类,但是我们却仍然通过到节点到节点之间的的距离,判断他们的对应关系。
1、如果节点x到节点y的距离为0时,此时代表为x和y同类。
2、如果节点x到节点y的距离为1时,此时代表为x吃y。
3、如果节点x到节点y的距离为2时,此时代表为x被y吃。
循环推断,因此可以得出节点到根节点的距离distance%3=0,1,2时,分别代表为根节点的同类、被根节点吃,吃根节点。任意两个节点只需要判断与根节点的关系,就能判断这两个节点之间的一个关系,演变为distance到根节点的距离,就可以判断两个节点之间的距离。

1、初始化
const int N = 100010;
int p[N], dist[N];// dist代表节点x到根节点的距离
//初始化并查集,全局变量dist已经自动初始化为0
for (int i = 1; i <= n; i++) p[i] = i;
2、压缩路径查找操作
//压缩路径查找
int find(int x) {
if (p[x] != x) {
//返回根节点,t暂存p[x]的根节点
int t = find(p[x]);
//上面find(p[x])递归一轮到根节点后,实际上dist[p[x]]存储的已经是p[x]到根节点的距离了
//类似与逐层递归上去,而dist[p[x]],也会递归的返回从根节点到p[x]的距离(可以递归模拟一下)
//x到新父节点(根节点,因为会压缩到根节点)的距离等于x到旧父节点的距离加上旧父节点到根节点的距离
dist[x] += dist[p[x]];
//将x的父节点也设置为根节点,达到压缩路径
p[x] = t;
}
return p[x];
}
3、合并图解

4、AC代码
#include<iostream>
using namespace std;
const int N = 100010;
// dist[x]始终记录的是的时x到p[x](父节点)的距离
//只不过一旦进行了压缩路径查找,路径上所有节点的父节点都会变为根节点
//故此时dist[x]就可以直接代表,x到根节点的路径
int p[N], dist[N];
//压缩路径查找
int find(int x) {
if (p[x] != x) {
//返回根节点,t暂存p[x]的根节点
int t = find(p[x]);
//上面find(p[x])递归一轮到根节点后,实际上dist[p[x]]存储的已经是p[x]到根节点的距离了
//类似与逐层递归上去,而dist[p[x]]也会一层一层的加上父节点到根节点的距离(可以递归模拟一下)
//x到新父节点(根节点,因为会压缩到根节点)的距离等于x到旧父节点的距离加上旧父节点到根节点的距离
dist[x] += dist[p[x]];
//将x的父节点也设置为根节点,达到压缩路径
p[x] = t;
}
return p[x];
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, k;
cin >> n >> k;
//初始化并查集,全局变量dist已经自动初始化为0
for (int i = 1; i <= n; i++) p[i] = i;
int res = 0;
while (k--) {
int op, x, y;
cin >> op >> x >> y;
if (x > n || y > n) {
res++;
}
else
{
int px = find(x), py = find(y);
//说的话是 x和y是同类
if (op == 1) {
//当x和y在同一个集合且不满足d[x]%3!=d[y]%3时,是假话
if (px == py && (dist[x] - dist[y]) % 3) {
res++;
}
else if (px != py) {
p[px] = p[py];
//dist[x] dist[px]
dist[px] = dist[y] - dist[x];
}
}
else
{
//当x和y在同一个集合且不满足d[x]%3!=(d[y]+1)%3时,是假话
if (px == py && ((dist[x] - dist[y] - 1) % 3)) res++;
else if (px != py) {
p[px] = p[py];
dist[px] = dist[y] + 1 - dist[x];
}
}
}
}
cout << res << '\n';
return 0;
}

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献3条内容
已为社区贡献3条内容





所有评论(0)