Uppaal 4.0完整教程(一)：定义,相关概念及工具包

本文是关于工具Uppaal的教程论文。其目标是对工具中实现的时钟自动机的特点进行简要介绍，本小节着重对时钟自动机定义，概念方面进行说明。

子不语zzh

1645人浏览 · 2024-01-18 16:54:24

子不语zzh · 2024-01-18 16:54:24 发布

Uppaal 4.0完整教程(一)：定义及相关概念

A Tutorial on Uppaal 4.0

Updated November 28, 2006

摘要

本文是关于工具Uppaal的教程论文。其目标是对工具中实现的时钟自动机的特点进行简要介绍，展示其界面，并解释如何使用该工具。本文的贡献在于提供参考示例和建模模式。

1 引言

Uppaal是由乌普萨拉大学和奥尔堡大学共同开发的用于实时系统验证的工具箱。它已成功应用于通信协议到多媒体应用等案例研究中[35,55,24,23,34,43,54,44,30]。该工具旨在验证可建模为时钟自动机网络的系统，这些自动机带有整数变量、结构化数据类型、用户定义的函数和通道同步。

Uppaal的第一个版本于1995年发布[52]，此后一直在不断发展[21,5,13,10,26,27]。实验和改进包括数据结构[53]、部分顺序减少[20]、Uppaal的分布式版本[17,9]、引导和最小成本可达性[15,51,16]、对UML Statecharts的研究[29]、加速技术[38]以及新的数据结构和内存减少[18,14]。版本4.0[12]引入了对称减少[36]、广义扫描线法[49]、新的抽象技术[11]、优先级[28]和用户定义的函数。Uppaal还涌现出相关的博士论文[50,57,45,56,19,25,32,8,31]。它具有Java用户界面和用C++编写的验证引擎，并可以免费获取，网址为http://www.uppaal.com/。

本教程涵盖了时钟自动机网络和Uppaal中使用的时钟自动机的特点，详见第2节。工具本身在第3节中描述，三个详细示例在第4、5和6节中讨论。最后，第7节介绍了通常与Uppaal一起使用的建模模式。

2 Uppaal中的时钟自动机

模型检测器Uppaal基于时钟自动机理论[4]（参见[42]中的自动机理论），其建模语言提供了额外的功能，如有界整数变量和紧迫性。Uppaal的查询语言，用于指定要检查的属性，是TCTL（定时计算树逻辑）[39,3]的子集。在本节中，我们介绍Uppaal的建模和查询语言，并对时钟自动机中的时间进行直观解释。

2.1 建模语言

时钟自动机网络 时钟自动机是一种有限状态机，带有时钟变量。它使用一种稠密时间模型，其中时钟变量评估为实数。所有时钟都同步进行。在Uppaal中，系统被建模为多个这样的时钟自动机并行运行的网络。该模型进一步使用有界离散变量，这些变量是状态的一部分。这些变量的用法类似于编程语言：它们被读取、写入，并且受到常见算术运算的影响。系统的状态由所有自动机的位置、时钟值和离散变量的值定义。每个自动机可以单独触发一个边（有时误称为过渡）或与另一个自动机同步[原文注：或在广播同步的情况下多个自动机，这是Uppaal中时钟自动机的另一个扩展。]，从而导致一个新的状态。

图1(a)显示了一个模拟简单灯的时钟自动机。

图1：简单灯(Lamp)的示例

灯有三个位置：关闭、低亮度和高亮度。如果用户按下按钮，即与press?同步，灯将打开。如果用户再次按下按钮，灯将关闭。然而，如果用户快速连按两次按钮，则灯将打开并变得明亮。用户模型显示在图1(b)中。用户可以在任何时候随机按下按钮，甚至根本不按按钮。灯的时钟 $y$ 用于检测用户是否快速（ $y < 5$ ）或慢速（ $y >= 5$ ）。我们提供了基本的时钟自动机语法和语义的定义。在接下来的内容中，我们将跳过Uppaal支持的更丰富的时钟自动机特性，即带有整数变量和urgent(紧急)和committed位置的扩展。有关更多信息，请参阅工具内的帮助菜单。

我们使用以下符号：

符号	说明
$C$	时钟的集合
$B (C)$	形式为 $\bowtie c$ 或 $\bowtie c$ 的简单条件的合取集合，其中 $\\x, y ∈ C$ ， $\mathbb{N}$ ， $\bowtie ∈ \{<, ≤, =, ≥, >\}$

时钟自动机是一个有限的有向图，用条件标注并重置非负实值时钟。

定义1（时钟自动机（TA））。时钟自动机是一个元组 $L, l_0, C, A, E, I)$ ，其中 $L$ 是位置集， $l_0$ ∈ $L$ 是初始位置， $C$ 是时钟集， $A$ 是动作、协动作(co-actions)和内部 $τ -$ 动作的集合， $E ⊆ L × A × B(C) × 2^C × L$ 是具有动作、保护条件和待重置时钟集的位置之间的边集， $I : L \to B (C)$ 为位置分配不变量。

在之前图1的例子中，y:=0 是时钟 $y$ 的重置，标签press? 和 press! 表示动作-协动作(action-co-action)（这里是通道同步）。

现在我们定义时钟自动机的语义。时钟估值是一个函数 $u : C → R_{≥0}$ ，它从时钟集映射到非负实数。让 $\mathbb{R}^C$ 是所有时钟估值的集合。对所有 $x \in C$ ，令 $u_0(x) = 0$ 。我们将滥用(abuse)符号，将保护条件(guards)和不变量(invariant)视为时钟估值集，记 $u \in I (l)$ 表示 $u$ 满足 $I (l)$ 。

定义2（TA的语义）。设 $L, l_0, C, A, E, I)$ 是一个时钟自动机。语义(semantics)定义为一个标记转换系统 $S, s_0, →>$ ，其中 : $\mathbb{R}^C$ 是状态集， $s_0 = (l_0, u_0)$ 是初始状态， $S×(\mathbb{R}_{≥0}∪A)×S$ 是转换关系，满足：

$if\ \forall\ d':0 ≤ d' ≤ d\Longrightarrow u + d' ∈ I(l)，则 (l, u) \stackrel{d}{→} (l, u + d)$ ，
$\ \exist\ e = (l, a, g, r, l') ∈ E 使得 u ∈ g, u' = [r \mapsto 0]u 且 u' ∈ I(l')，则 (l, u) \stackrel{a}{→} (l', u')$ 。

其中对于 $\mathbb{R}_{≥0}$ ， $u + d$ 将 $C$ 中的每个时钟 $x$ 映射到值 $u (x) + d$ ， $\mapsto0]u$ 表示将 $r$ 中的每个时钟映射为 0 并在 $\ r C \backslash r$ 上与 $u$ 一致的时钟估值。图2说明了TA的语义。

图2：时钟自动机的语义：从给定初始状态的不同转变(transition)

从给定的初始状态出发，我们可以选择采取一个动作或延迟转换（这里有不同的值）。根据所选择的延迟，可能会禁止进一步的动作。

时钟自动机通常组合成一个共享时钟和动作集的时钟自动机网络，由 $n$ 个时钟自动机 $\mathcal{A}_i= (L_i, l^0_i, C, A, E_i, I_i)$ ， $1 \leq i \leq n$ 组成。位置向量是一个向量 $\bar{l} = (l_1, ..., l_n)$ 。我们将不变量函数组合成一个关于位置向量的公共函数 $I(\bar{l}) = ∧_iI_i(l_i)$ 。我们写 $\bar{l}[l'_i/l_i]$ 表示将向量中的第 $i$ 个元素 $l_i$ 替换为 $l'_i$ 。下面我们定义时钟自动机网络的语义。

定义3（时钟自动机网络的语义）。设 $\mathcal{A}_i = (L_i, l^{0}_i, C, A, E_i, I_i)$ 是 $n$ 个时钟自动机的网络。设 $\bar{l}_0 = (l^0_1, ..., l^0_n)$ 是初始位置向量。语义定义为一个转换系统 $S, s_0, →>$ ，其中 $(L_1 × ··· × L_n) × \mathbb{R}^C$ 是状态集， $s_0 = (\bar{l}_0, u_0)$ 是初始状态， $\to\subseteq S \times S$ 是由以下定义的转换关系：

$if\ \forall\ d':0 ≤ d' ≤ d\Longrightarrow u + d' ∈ I(\bar{l})，则 (\bar{l}, u) \stackrel{d}{→} (\bar{l}, u + d)$
$if\ \exist\ l_i \stackrel{τgr} {→} l'_i\ 使得\ u ∈ g\ ,u' = [r \mapsto 0]u$ 且 $I(\bar{l}[l'_i/l_i])，则(\bar{l}, u) \stackrel{a}{→} (\bar{l}[l'_i/l_i], u')$
$if\ \exist\ l_i \stackrel{c?g_ir_i}{→} l'i 和\ l_j \stackrel{c!g_jr_j} {→} l'_j 使得\ u ∈ (g_i ∧ g_j)，u' = [r_i ∪ r_j \mapsto 0]u 且 u' ∈ I(\bar{l}[l'_j/l_j, l'_i/l_i])，则 (\bar{l}, u) \stackrel{a}{→} (\bar{l}[l'_j/l_j, l'_i/l_i], u')$

作为语义的一个例子，图1中的灯可能有以下状态（我们跳过用户）：
$(L am p . o ff, y = 0) \to (L am p . o ff, y = 3) \to$
$(L am p . l o w, y = 0) \to (L am p . l o w, y = 0.5) \to$
$(L am p . b r i g h t, y = 0.5) \to (L am p . b r i g h t, y = 1000) ...$

在 Uppaal 中的时钟自动机 Uppaal 建模语言通过以下附加功能扩展了时钟自动机（参见图 3：

图3：常量和变量的声明，以及在第4 节列车门示例的两个模板之间一些通道同步和一些committed位置的示意图

模板(Templates) 自动机是用一组参数定义的，这些参数可以是任何类型的（例如， $in t$ ， $c han$ ）。这些参数在过程声明中替换为给定的参数。

常量(Constants) 被声明为 const name value。根据定义，常量不能被修改，并且必须具有整数值。

有界整数变量(Bounded integer variables) 被声明为 int[min,max] name，其中 $min$ 和 $ma x$ 分别是下界和上界。守卫(guard)、不变量(invariant)和赋值(assignment)可能包含范围在有界整数变量上的表达式。在验证时检查这些界限，违反界限会导致无效状态被丢弃（在运行时）。如果省略界限，则使用默认范围 -32768 到 32768。

二进制同步通道(Binary synchronisation) 被声明为 chan c。标记为 c! 的边与标记为 c? 的边同步。如果启用了几种组合，则非确定性地选择同步对。

广播通道(Broadcast channels) 被声明为 broadcast chan c。在广播同步中，一个发送者 c! 可以与任意数量的接收者 c? 同步。任何当前状态下可以同步的接收者都必须这样做。如果没有接收者，那么发送者仍然可以执行 c! 动作，即广播发送永远不会阻塞。

Urgent 同步(Urgent synchronisation) 通道通过在通道声明前加上关键字 urgent 来声明。如果在Urgent通道上启用了同步转换，则不得发生延迟。使用urgent通道进行同步的边不能有时间约束，即不允许时钟守卫。

Urgent 位置(Urgent locations) 在语义上等同于添加一个额外的时钟 $x$ ，该时钟在所有进入边上重置，并且在该位置具有不变量x<=0。因此，当系统处于Urgent位置时，不允许时间流逝。

Committed 位置(Committed locations) 对执行的限制比Urgent位置更严格。如果状态(state)中的任何位置是Committed的，则该状态为Committed状态。committed状态不能延迟，下一个转换必须涉及至少一个committed位置的外出边。

数组(Arrays) 时钟、通道、常量和整数变量允许使用数组。它们是通过在变量名后附加大小来定义的，例如 chan c[4]; clock a[2]; int[3,5] u[7];。

初始化器(Initialisers) 用于初始化整数变量和整数变量数组。例如，int i = 2; 或 int i[3] = {1, 2, 3};。

记录类型(Record types) 使用 C 语言中的 struct 构造声明。

自定义类型(Custom types) 使用类似 C 语言的 typedef 构造定义。您可以从其他基本类型（例如记录）定义任何自定义类型。

用户函数(User functions) 可以在模板内全局定义或局部定义。模板参数可以从局部函数访问。语法类似于 C，但没有指针。C++ 语法支持仅用于参数的引用。

在 Uppaal 中的表达式 Uppaal 中的表达式涉及时钟和整数变量。BNF 在附录中的图 33 中给出。
图33

图33：BNF（巴科斯-瑙尔范式）中表达式的语法

表达式与以下标签一起使用：

选择(Select) 选择标签包含以逗号分隔的 name : type 表达式列表，其中 name 是变量名，type 是定义的类型（内置或自定义）。这些变量只能在关联的边上访问，并且它们将在其各自类型的范围内取一个非确定性值。

守卫(Guard) 守卫是满足以下条件的特殊表达式：它是无副作用的；它评估为布尔值；仅引用时钟、整数变量和常量（或这些类型的数组）；时钟(clocks)和时钟差(clock difference)仅与整数表达式比较；时钟上的守卫本质上是合取conjunctions（允许对整数条件进行析取disjunctions）。守卫可以调用返回 bool 的无副作用函数，尽管此类函数不支持时钟约束。

同步(Synchoronisation)：同步标签要么是Expression!的形式，要么是Expression?的形式，或者是一个空标签。表达式必须没有副作用，计算结果为一个通道，并且只能引用整数、常数和通道。

更新(Update)：更新标签是一个以逗号分隔的表达式列表，带有副作用；表达式只能引用时钟、整数变量和常数，并且只能给时钟赋整数值。它们也可以调用函数。

不变量(Invariant)：不变量是满足以下条件的表达式：它没有副作用；只引用时钟、整数变量和常数；它是形式为x<e或x<=e的条件的合取，其中 $x$ 是时钟引用， $e$ 计算为整数。不变量可以调用返回 bool 的无副作用函数，尽管这样的函数不支持时钟约束。

2.2 查询语言

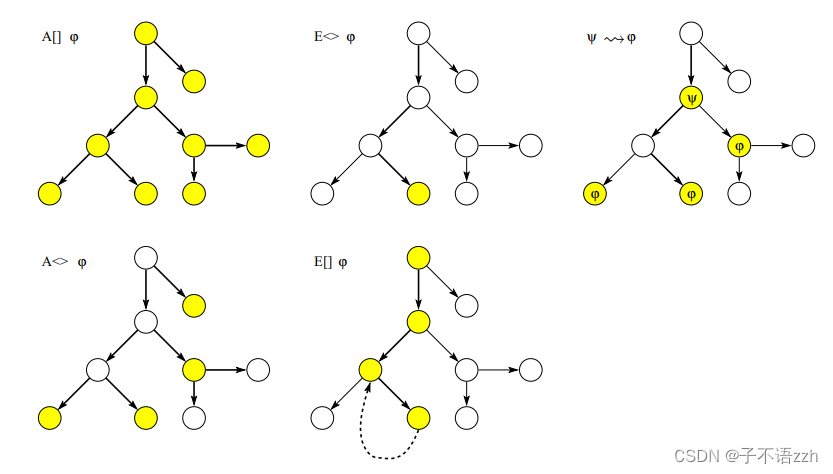
模型检查器(model-checker)的主要目的是验证模型是否符合需求规范。像模型一样，需求规范必须用形式化明确且机器可读的语言表达。科学文献中存在几种这样的逻辑，Uppaal使用的是TCTL的简化版本。与TCTL一样，查询语言由路径公式(path formula)和状态公式(state formula)组成。状态公式描述单个状态，而路径公式则量化模型的路径或轨迹。路径公式可以分为可达性、安全性和活性。图4展示了Uppaal支持的不同路径公式。每种类型在下文中有所描述。

图 4：Uppaal 支持的路径公式。填充的状态表示满足给定状态公式 φ 的状态。粗体边用于显示公式评估的路径

【译者注：在这里插入图片描述
这里面的最终 eventually我的理解是在某路径的某个后续节点上
】

状态公式(State Formula) 状态公式是一个表达式（见图33），可以在不考虑模型行为的情况下针对某个状态进行评估。例如，这可能是一个简单的表达式，比如i == 7，在i等于7时该表达式在某状态下为真。状态公式的语法是守卫的超集，即状态公式是一个无副作用的表达式，但与守卫不同的是，使用分支的方式没有限制。也可以使用表达式P.l来测试特定进程是否处于给定位置，其中P是一个进程，l是一个位置。

在 Uppaal 中，死锁(deadlock)使用特殊的状态公式表示（尽管这严格来说不是状态公式）。该公式仅由关键字deadlock组成，适用于所有死锁状态。如果一个状态本身或其任何延迟后继都没有外出动作转换，则该状态是死锁状态。由于Uppaal当前的限制，死锁状态公式只能与可达性和不变性路径公式一起使用（见下文）。

可达性属性(Reachability Properties) 可达性属性是最简单的属性形式。它们询问是否有任何可达状态可能满足给定的状态公式φ。另一种表述方式是：是否存在一条从初始状态开始的路径，使得沿该路径,φ最终得到满足。在设计模型时，经常使用可达性属性进行完整性检查。例如，在创建涉及发送者和接收者的通信协议模型时，询问发送者是否有可能发送消息，或者消息是否可能被接收，是有意义的。这些属性本身并不保证协议的正确性（即任何消息最终都会被传递），但它们验证了模型的基本行为。

我们使用路径公式E ◊ φ来表示某个满足φ的状态应该是可达的。在Uppaal中，我们使用语法E<> ϕ来写这个属性。

安全属性(Safety Properties) 安全属性的形式是：“某些坏事永远不会发生”。例如，在核电站模型中，一个安全属性可能是操作温度始终（不变地）在某个阈值以下，或者熔毁永远不会发生。这种属性的一个变体是“某些事情可能永远不会发生”。例如，在玩游戏时，一个安全状态是我们仍然可以赢得游戏的状态，因此我们可能不会输。

在Uppaal中，这些属性被积极地表述，例如，某些好事始终为真。让φ成为一个状态公式。我们用路径公式 A□φ[注3：A□φ=¬E⋄¬φ]来表达φ在所有可达状态中应该为真，而E□φ则表示应该存在一条最大路径，使得φ始终为真。在Uppaal中，我们分别写作A[] φ和E[] φ。

活性属性(Liveness Properties) 活性属性的形式是：某些事情最终会发生，例如，按下遥控器的开关后，电视最终应该打开。或者在通信协议模型中，任何已发送的消息最终都应该被接收。
活性在其简单形式中用路径公式A ⋄ φ表达，意味着φ最终会得到满足。更有用的形式是引导或响应属性，写作φ ⇝ ψ，读作每当φ得到满足时，最终ψ也会得到满足，例如，每当发送消息时，最终它将被接收。
在Uppaal中，这些属性分别写作A<> φ和φ --> ψ。

2.3 理解时间

不变量和守卫(Invariants and Guards) Uppaal使用连续时间模型。我们用一个简单的例子来说明时间的概念，该例子使用观察者(observer)来进行说明。通常，观察者是一个负责检测事件而不改变被观察系统的附加自动机。在我们的例子中，时钟重置（x:=0）被委派给观察者，用于说明目的。

图5：带有观察者的第一个例子

图5展示了第一个模型及其观察者。我们有两个并行的自动机。第一个自动机有一个自循环，由x>=2（x是一个时钟）守卫，与第二个自动机上的reset通道同步。第二个自动机，即观察者，检测自循环边何时被采用，然后回到空闲状态并重置时钟x。我们将x的重置从自循环移至观察者，只是为了测试重置之前的转换发生了什么。注意，taken位置被标记为c（committed），以避免在该位置延迟。

以下属性可以在Uppaal中验证（参见第3节以了解界面概述）。假设我们将观察者自动机命名为Obs，我们有：

$A[]\ Obs.taken\ imply\ x>=2$ ：【译者注：imply关键字表示蕴含关系】所有对x的重置都发生在x大于2时。这个查询意味着在所有可达状态中，处于Obs.taken位置意味着x>=2。
$E<>\ Obs.idle\ and\ x>3$ ：这个属性要求，有可能达到一个状态，其中Obs处于空闲位置并且x大于3本质上我们检查我们是否可能在重置之间至少延迟3个时间。对于更大的值，如30000，结果也是一样的，因为这个模型中没有不变量。

我们更新第一个模型，在loop位置添加一个不变量，如图6所示。

图6：带有不变量的更新后的示例。观察者与图5中的相同，这里未显示

该不变量是一个进度条件：系统不允许在该状态停留超过3个时间单位，以便必须采取转换并在我们的例子中重置时钟。现在时钟x有3作为上限。以下属性成立：

$A[]\ Obs.taken\ imply\ (x>=2\ and\ x<=3)$ 表明当x在2和3之间时将采取转换，即在2到3的延迟后。
$E<>\ Obs.idle\ and\ x>2$ ：当x在2到3之间时，可以采取转换。使用下一个属性检查3的上限。
$A[]\ Obs.idle\ imply\ x<=3$ ：表明上限得到了遵守。

之前的属性 $E<>\ Obs.idle\ and\ x>3$ 不再成立。

现在，如果我们移除不变量并将守卫条件改为 x>=2 and x<=3，你可能会认为这和之前一样，但其实并非如此！系统没有进展条件(progress condition)，只是守卫条件有所变化。图 7 展示了发生的情况：

图7：更新守卫无不变量的例子

系统可能采取与之前相同的转换，但也可能发生死锁。如果系统在 3 个时间单位后没有进行转换，那么系统可能会陷入停滞。实际上，系统不符合 A[] not deadlock 的属性。属性 A[] Obs.idle imply x<=3 不再成立，死锁也可以通过属性A[] x>3 imply not Obs.taken 来说明，即在 3 个时间单位后，转换不再被采取。

Committed 位置和 Urgent 位置 在 Uppaal 中有三种不同类型的位置：带或不带不变量的普通位置（例如，前例中的 x<=3），urgent位置和committed位置。图 8 展示了三个自动机来说明它们之间的区别。

图8：并行自动机，具有 normal、 urgent 和 committed 状态。时钟是局部的，即 P0.x 和 P1.x 是两个不同的时钟

标记为 u 的位置是urgent的，而标记为 c 的位置是committed的。自动机中的时钟是局部的，即 P0 中的 x 与 P1 中的 x 不同。

为了理解普通位置和urgent位置之间的区别，我们可以观察到以下属性成立：

$E<>\ P0.S1\ and\ P0.x>0$ ：在 P0 的 S1 中等待是可能的。
$A[]\ P1.S1\ imply\ P1.x==0$ ：在 P1 的 S1 中等待是不可能的。

urgent位置相当于带有重置指定时钟 y 并标记有不变量 y<=0 的入边的位置【译者注：意思为自带一条有这些东西的入边】。在urgent状态中，时间可能不会前进，但允许与普通状态的交错。

committed位置更具限制性：在所有 P2.S1 激活的状态中（在我们的例子中），唯一可能的转换是触发从 P2.S1 出去的边。一个激活了committed位置的状态被称为committed状态：不允许延迟，且必须在后继状态（或如果有多个committed位置，则为其中之一）离开committed位置。

3 Uppaal 工具包概览

Uppaal使用客户端-服务器架构，将工具分为图形用户界面和模型检查引擎。用户界面（即客户端）是用Java实现的，而引擎（即服务器）则为不同平台（Linux、Windows、Solaris）编译。正如名称所暗示的，这两个组件可以在不同的机器上运行，因为它们通过TCP/IP进行通信。还有一个独立的引擎版本，可以在命令行上使用。

3.1 Java客户端

这个工具背后的想法是使用图形编辑器对系统进行时钟自动机建模，通过模拟来验证其行为是否符合预期，最后验证它是否满足一组属性。Java客户端的图形界面（GUI）体现了这一想法，分为三个主要部分：编辑器、模拟器和验证器，通过三个“标签页”访问。

编辑器(The Editor) 一个系统被定义为并行放置的时钟自动机网络，这些自动机在工具中称为进程。一个进程是从带参数的模板实例化的。编辑器分为两部分：一个树形窗格用于访问不同的模板和声明，以及一个绘图画布/文本编辑器。图9展示了第4节中的火车闸门示例的编辑器。

图9：火车道闸示例中的列车自动机。在工具栏中选择按钮已激活。在此模式下，用户可以移动位置和边，或编辑标签。其他模式用于添加位置、边和边上的顶点（称为钉子）。新位置默认没有名称。两个文本字段允许用户定义模板名称及其参数。有用的技巧：中间鼠标按钮是添加新元素的快捷方式，即在画布、位置或边上按下它会分别添加新位置、边或钉子

位置用名称和不变量标记，边用守卫条件（例如，e == id）、同步（例如，go?）和赋值（例如，x:=0）标记。

左侧的树形结构可访问系统描述的不同部分：

全局声明 包含全局整数变量、时钟、同步通道和常量。

模板火车、门和IntQueue是不同的带参数时钟自动机。模板可能有变量、通道和常量的本地声明。

进程分配 将模板实例化为进程。进程分配部分包含这些实例的声明。

系统定义 系统中的进程列表。

标签和声明中使用的语法在工具的帮助系统中有描述。本地和全局声明显示在图10中。

图10

图10：火车道闸示例的不同本地和全局声明。我们叠加了几个工具的屏幕截图，以紧凑的方式展示这些声明

图形语法直接源于第2节中时钟自动机的描述。

模拟器(The Simulator) 模拟器有三种使用方式：用户可以手动运行系统并选择要采取的转换，可以切换到随机模式让系统自行运行，或者用户可以通过跟踪（保存或从验证器导入）来查看某些状态是如何可达的。图11展示了模拟器。

图11

图11. 火车道闸示例的模拟器选项卡视图。在变量面板中对约束系统的解释取决于是否选择了转换面板中的某个转换。如果没有选择任何转换，那么约束系统将显示沿路径可以达到的所有可能的时钟赋值。如果选择了一个转换，那么只会显示可以从中进行转换的时钟赋值。在不使用鼠标进行模拟器导航的情况下的键盘绑定可以在集成的帮助系统中找到

它分为四个部分：

控制部分用于选择和触发启用的转换，通过跟踪，切换随机模拟。
变量视图显示整数变量的值和时钟约束。Uppaal不显示具有实际时钟值的具体状态。由于这样的状态有无限多个，Uppaal反而显示称为符号状态(symbolic state)的具体状态集。一个符号状态中的所有具体状态共享相同的位置向量和离散变量的相同值。时钟的可能值由一组约束描述。符号状态中的时钟验证正是满足所有约束的那些。
系统视图显示当前状态的所有实例化自动机和活动位置。
消息序列图显示不同进程之间的同步以及每一步的活动位置。

验证器(The Verifier) 图12展示了验证器的“标签页”。

图12

图12：火车闸门示例的验证标签页视图

属性可以在概览列表中选择。用户可以对一个或多个属性进行模型检查，插入或移除属性，并切换视图以查看列表中的属性或评论。选择一个属性时，可以编辑其定义（例如，E<> Train1.Cross and Train2.Stop …）或评论以非正式地记录属性的含义。底部的状态面板显示与服务器的通信。

当启用跟踪生成并且模型检查器找到一个跟踪时，会询问用户是否想将其导入模拟器。满足的属性标记为绿色，违反的标记为红色。如果在选项菜单中选择了过度近似或不足近似，则可能发生在所使用的近似下验证是不确定的情况。在这种情况下，属性被标记为黄色。

3.2 独立验证器

在执行大型验证任务时，从GUI内部执行这些任务往往很麻烦。对于这种情况，称为verifyta的命令行独立验证器更合适。它还使在内存充足的远程UNIX机器上运行验证变得容易。它接受所有在GUI中可用的选项的命令行参数，请参见附录中的表3。

表3. verifyta 的选项及其在 GUI 中的相应选项。verifyta 的默认选项以粗体显示

【该表翻译如下：

状态空间表示

-C DBM
在用于存储可达状态的状态表示中，使用DBM（差分约束矩阵）而不是最小约束图[53]。这会增加内存使用量（在有许多时钟的模型中尤其如此），但通常更快。
-A 过度近似
使用凸包过度近似[7]。对于时序系统，这可以大幅提高验证速度。对于非时序系统，这没有效果。
-Z 不足近似
使用位状态哈希不足近似。这将内存消耗减少到或多或少固定的量。通过改变哈希表大小来控制近似的精度。在[40,41]中称为超迹。
-T 重用
通过在可能时重用生成的状态空间来加速验证。对于某些属性的组合，此选项可能导致更大的状态空间表示，从而抵消加速效果。
-U 当使用最小约束图表示状态时，此选项改变了状态的比较方式。它以更耗时的比较运算符为代价来减少内存消耗。减少的内存使用可能会抵消开销。在GUI中，这个选项始终开启。
-H 改变验证期间使用的哈希表大小。可以为大型系统提供加速。

状态空间缩减