4.5-1

对下列递归式，使用主方法求出渐进紧确界

解：

a. $T(n)=2T(n/4)+1$

根据主定理

$$a=2,b=4,f(n)=1,n^{{\log }_{b}a}=n^{{\log }_{4}2}=n^{0.5}$$
对于常数$ϵ=0.5$,有
$$f(n)=1=O(n^{{\log }_{b}a-ϵ})=O(n^{0.5-0.5})=O(1)$$

符合主定理情况1，所以$T(n)=\Theta (n^{{\log }_{b}a})=\Theta (\sqrt{n})$。

b. $T(n)=2T(n/4)+\sqrt{n}$

根据主定理
$$a=2,b=4,f(n)=\sqrt{n},n^{{\log }_{b}a}=n^{{\log }_{4}2}=\sqrt{n}$$
所以
$$f(n)=\sqrt{n}=\Theta (n^{{\log }_{b}a})=\Theta (\sqrt{n})$$
符合主定理情况2，所以$T(n)=\Theta (n^{{\log }_{b}a}\lg n)=\Theta (\sqrt{n}\lg n)$。

c. $T(n)=2T(n/4)+n$

根据主定理
$$a=2,b=4,f(n)=n,n^{{\log }_{b}a}=n^{{\log }_{4}2}=\sqrt{n}$$
对于常数$ϵ=\frac{1}{2}$,有$f(n)=n=\Omega (n^{{\log }_{b}a+ϵ})=\Omega (n)$，且对于$\frac{1}{2}\le c<1$,满足：
$$af(n/b)=2f(n/4)=2\ast \frac{n}{4}=\frac{n}{2}\le cf(n)=cn$$
符合主定理情况3，所以$T(n)=\Theta (f(n))=\Theta (n)$。

d. $T(n)=2T(n/4)+n^2$

根据主定理
$$a=2,b=4,f(n)=n^2,n^{{\log }_{b}a}=n^{{\log }_{4}2}=\sqrt{n}$$
对于常数$ϵ=\frac{3}{2}$,有$f(n)=n^2=\Omega (n^{{\log }_{b}a+ϵ})=\Omega (n^2)$，且对于$\frac{1}{8}\le c<1$,满足
$$af(n/b)=2f(n/4)=2\ast \frac{n^2}{16}=\frac{n^2}{8}\le cf(n)=cn$$
符合主定理情况3，所以$T(n)=\Theta (f(n))=\Theta (n^2)$。

4.5-4

主方法能应用于递归式$T(n)=4T(n/2)+n^2\lg n$吗？请说明为什么可以或者为什么不可以。给出这个递归式的一个渐进上界。
《算法导论》中给出如下形式的主定理

因为
$$f(n)=n^2\lg n\ne \Theta (n^2)\ne O(n^{2-ϵ})\ne \Omega (n^{2+ϵ})$$
不满足上述三种情况的任何一种

$a=4,b=2,f(n)=n^2\lg n,n^{{\log }_{b}a}=n^{{\log }_{2}4}=n^2$
$n^2\lg n$渐进大于$f(n)$,但它不是多项式意义上的大于。

对于任意正常数$ϵ,f(n)/n^{{\log }_{b}a}=(n^2\lg n)/n^2=\lg n$均渐进小于$n^{ϵ}$。

因此主方法不能应用于此递归式。

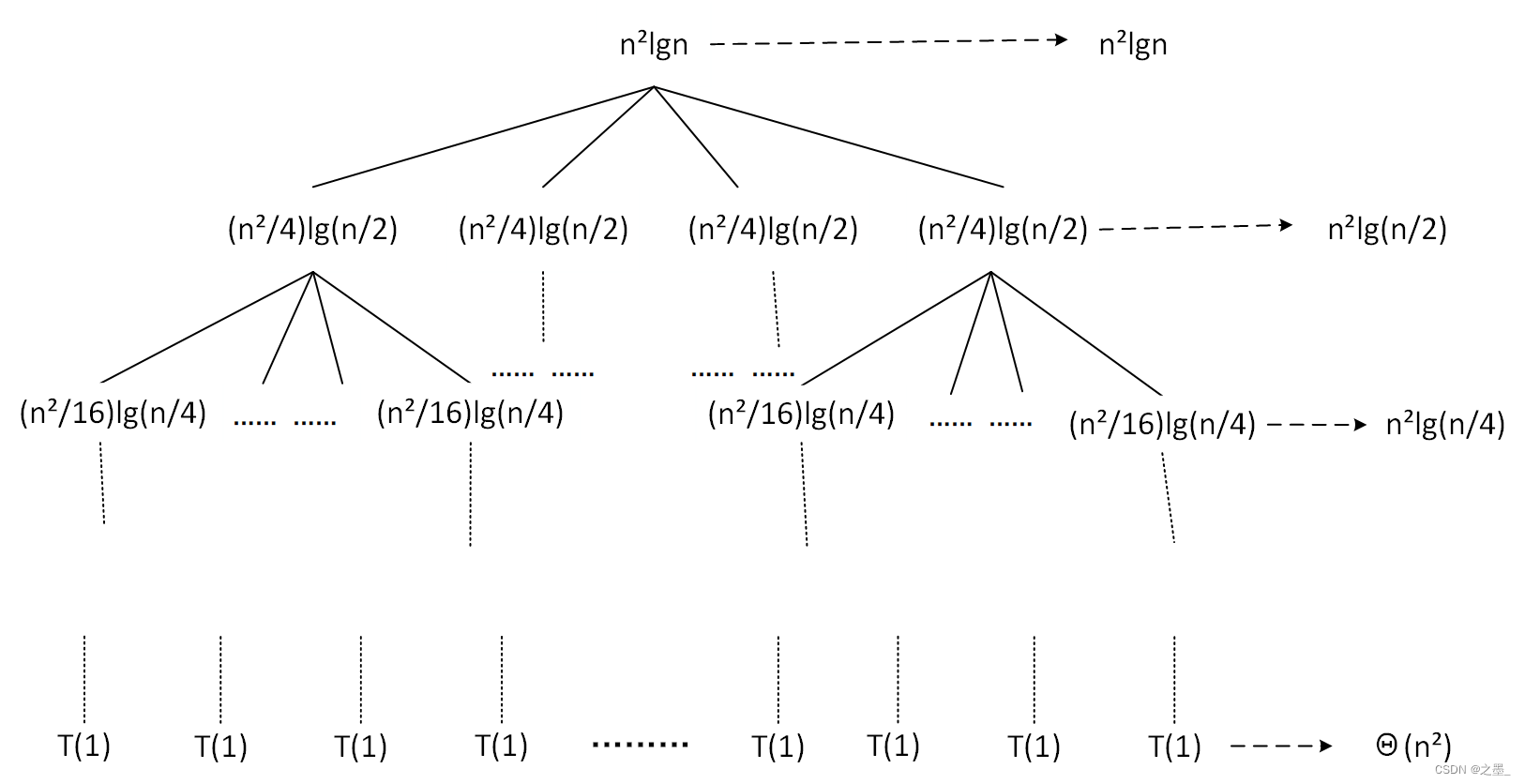
创建上述递归式的对应递归树如下

​ 在递归树中，深度为$i$的结点对应规模为$n/2^i$。当$n/2^i=1$时，即$i={\log }_{2}n$时，子问题规模变为$1$，对应叶结点$T(1)$，因此递归树高度为${\log }_{2}n$，有${\log }_{2}n+1$层。
​ 每层的结点数都是上一层的$4$倍，因此深度为$i$ 的结点数为$4^i$。深度为$i$的结点对应规模为$n/2^i$的子问题。因为每一层子问题规模都是上一层的$1/4$,所以对$i=0,1,2,\dots ,{\log }_{2}n-1$,深度为$i$的每个结点的代价为$(n/2^i{)}^2\ast \lg (n/2^i)$。因此对于对$i=0,1,2,\dots ,{\log }_{2}n-1$,深度为$i$的所有结点的总代价为$4^i(n/2^i{)}^2\ast \lg (n/2^i)=n^2\ast \lg (n/2^i)$。树的最底层深度为$ \log_2n$，有$4^{{\log }_{2}n}=n^2$个结点，每个结点的代价为$T(1)$，总代价为$n^2$，即$\Theta (n^2)$,确定整棵树的代价：
$$\begin{array}{rl}T(n)& =n^2\lg n+n^2\lg \frac{n}{2}+\dots +\Theta (n^2)\\ & =\sum _{i=0}^{{\log }_{2}n-1}{n}^2\lg (\frac{n}{2^i})+\Theta (n^2)\\ & =\frac{1}{2}{n}^2{\lg }^{2}n+\Theta (n^2)\\ & =O(n^2{\lg }^{2}n)\end{array}$$
​ 由此，对于原始递归式推导出一个猜测$T(n)=O(n^2{\lg }^{2}n)$。使用代入法验证猜测，即验证$T(n)=O(n^2{\lg }^{2}n)$是递归式$T(n)=4T(n/2)+n^2\lg n$的一个上界。即要证明：存在正常数$c$，使得$T(n)\le c{n}^2{\lg }^{2}n$对足够大的$n$都成立。

$n=1$时，$T(1)=1,c{n}^2{\lg }^{2}n=0$，$c$取任何值$T(n)\le c{n}^2{\lg }^{2}n$均不成立

$n=2$时，$T(2)=4T(1)+1^2\lg 1=4$，令$c\ge 1$即可使$T(n)\le c{n}^2{\lg }^{2}n$

$n\ge 3$时，假设$T(n)\le c{n}^2{\lg }^{2}n$对$n=3,4,\dots ,n$均成立，则有
$$\begin{array}{rl}T(n)& =4T(n/2)+n^2\lg n\\ & \le 4c(\frac{n}{2}{)}^2{\lg }^2\frac{n}{2}+n^2\lg n\\ & =c{n}^2(\lg n-\lg 2{)}^2+n^2\lg n\\ & =c{n}^2{\lg }^{2}n-2c{n}^2\lg (2+n)+n^2\lg n+c{n}^{2}l{g}^{2}2\\ & \le c{n}^2{\lg }^{2}n\end{array}$$
​ 即证明$c{n}^2{\lg }^{2}n-2c{n}^2\lg (2+n)+n^2\lg n+c{n}^{2}l{g}^{2}2\le c{n}^2{\lg }^{2}n$对某个常数$c>0$成立。

对上式进行变换
$$\begin{array}{r}\frac{\lg n}{2\lg (2+n)-l{g}^{2}2}=\frac{1}{2\lg 2-\frac{{\lg }^{2}2}{\lg n}}\le c\end{array}$$

$n\ge 3$时，$\frac{1}{2\lg 2-\frac{{\lg }^{2}2}{\lg n}}$是单调递减的，并且$n=3$时取得最大值$\frac{1}{2\lg 2-\frac{{\lg }^{2}2}{\lg 3}}$。结合$n=1,n=2$的情况，可知存在一个正常数$c$，使得$T(n)\le c{n}^2{\lg }^{2}n$对足够大的$n$都成立。

因此递归式的一个上界为$T(n)=O(n^2{\lg }^{2}n)$。

主定理另一种形式

对上述问题，《算法导论》中给出的主定理无法求解，但如下形式的主定理可以求解，其符合下述主定理的的第二种情况。

因为
$$\begin{gathered} \text{for k=1≥0} \\ f(n)=n^2\lg n=\Theta (n^2{\lg }^{1}n)=\Theta (n^2{\lg }^{2}n) \end{gathered}$$
所以符合情况$2$，存在一个上界$\Theta (n^2{\lg }^{2}n)$