使用牛顿法求解非线性方程
牛顿法,也称为牛顿-拉弗森方法,是一种强大的数值算法,用于快速找到函数的零点,即求解f(x)=0的x值。这个方法特别适用于求解复杂的非线性方程,其中解析解可能难以找到或者不存在。牛顿法的关键优势在于它的收敛速度非常快,尤其是当初始猜测接近实际解时。本文详细介绍了牛顿法的基本思想并使用此方法解决了一个实际问题,同时给出了基于此方法的MATLAB代码。
牛顿法的介绍
牛顿法,也称为牛顿-拉弗森方法,是一种强大的数值算法,用于快速找到函数的零点,即求解 f ( x ) = 0 f(x)=0 f(x)=0的 x x x值。这个方法特别适用于求解复杂的非线性方程,其中解析解可能难以找到或者不存在。牛顿法的关键优势在于它的收敛速度非常快,尤其是当初始猜测接近实际解时。
基本原理
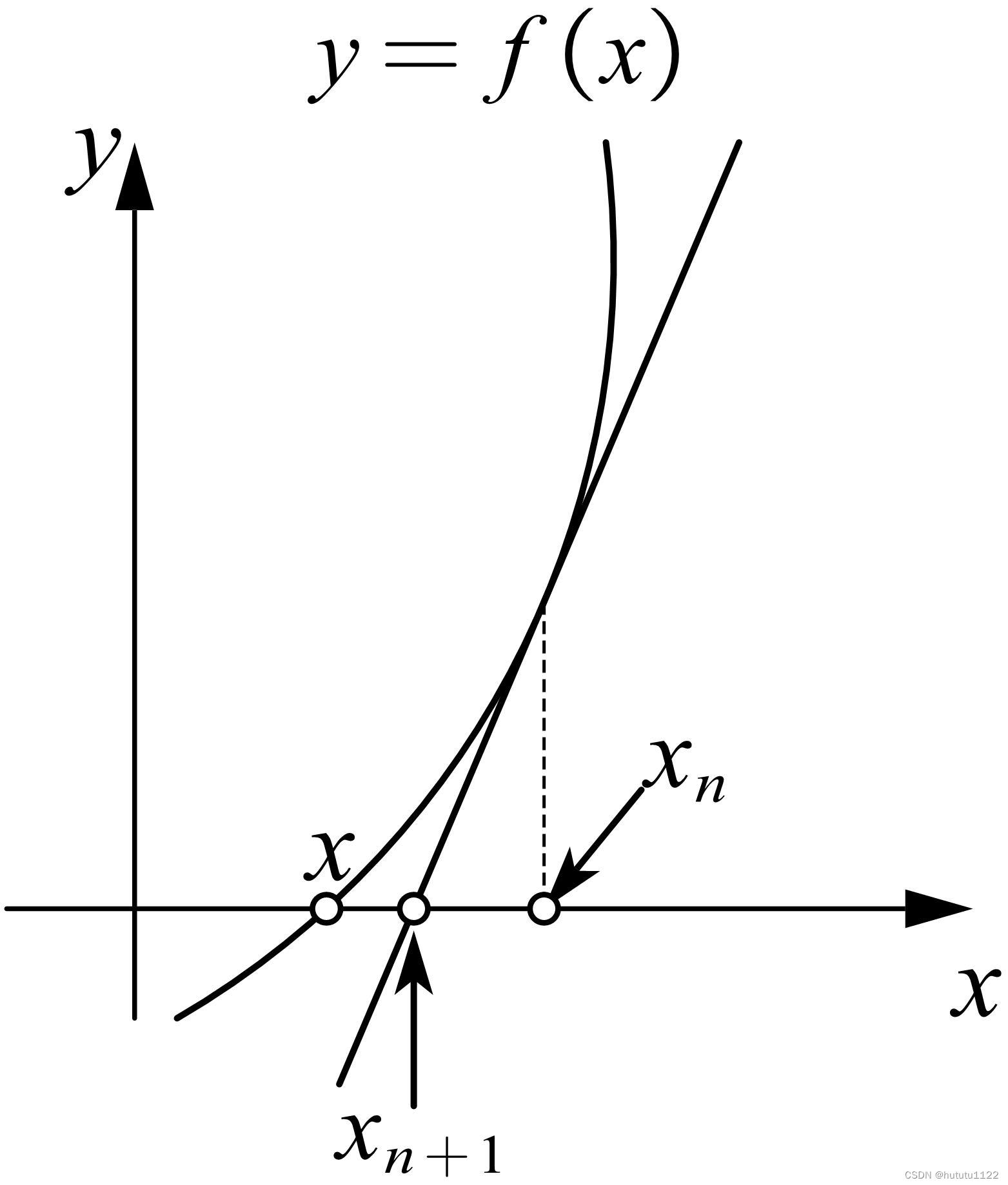
牛顿法的基本思想是利用函数在某点的线性近似来预测函数的根。如下图所示:

给定一个近似解
x
n
x_n
xn ,你可以找到函数在这一点的切线,然后看这条切线与x轴的交点
x
n
+
1
x_{n+1}
xn+1。这个交点作为下一个近似解。数学上,这个过程可以用以下公式描述:
x
n
+
1
=
x
n
−
f
(
x
n
)
f
′
(
x
n
)
x_{n+1}=x_n-\frac{f(x_n)}{f^{\prime}(x_n)}
xn+1=xn−f′(xn)f(xn)
这里,
f
′
(
x
n
)
f^{\prime}(x_n)
f′(xn)是函数
f
f
f在
x
n
x_n
xn处的导数。
迭代过程
1、选择初始猜测
x
0
x_0
x0:这是迭代过程的起点。理想的初始猜测应该尽可能接近实际解,但是牛顿法对初始猜测的准确度要求不是非常高。
2、计算函数值和导数:在当前猜测点
x
n
x_n
xn处计算函数
f
(
x
n
)
f(x_n)
f(xn)和其导数
f
′
(
x
n
)
f^{\prime}(x_n)
f′(xn)。
3、更新猜测:使用上面的迭代公式计算下一个猜测
x
n
+
1
x_{n+1}
xn+1。
4、检查收敛条件:如果
∣
x
n
+
1
−
x
n
∣
∣x_{n+1}-x_n∣
∣xn+1−xn∣小于预定的容忍度
ϵ
ϵ
ϵ,则认为找到了足够精确的解,迭代结束。
5、重复:如果未达到收敛条件,则使用新的$x_{n+1} $重复步骤 2 至 4,直到满足收敛条件或达到最大迭代次数。
特点和考虑事项
1、快速收敛:在好的初始猜测和函数性质允许的情况下,牛顿法可以非常快速地收敛到精确解。
2、依赖导数:需要计算函数的导数,对于某些复杂函数,可能会相对困难。
3、可能的失败:如果
f
′
(
x
n
)
=
0
f^{\prime}(x_n)=0
f′(xn)=0,则迭代公式无法应用,需要选择新的初始猜测。此外,如果初始猜测太远离真实解,或者函数在求解区域内行为怪异,牛顿法可能不会收敛。
实例:求解复杂非线性方程
考虑非线性方程
f
(
x
)
=
c
o
s
(
x
)
−
x
3
f(x)=cos(x)-x^3
f(x)=cos(x)−x3。目标是找到这个方程的一个根。
1、函数及其导数:
f
(
x
)
=
c
o
s
(
x
)
−
x
3
f(x)=cos(x)-x^3
f(x)=cos(x)−x3
f
′
(
x
)
=
−
sin
(
x
)
−
3
x
2
f^{\prime}(x)=-\sin(x)-3x^2
f′(x)=−sin(x)−3x2
2、初始猜测:假设
x
0
=
0.5
x_0=0.5
x0=0.5作为起始点。
3、迭代更新:应用牛顿法迭代公式寻找根。
解决此实例的MATLAB代码
function [x,i] = newtonMethodExample()
% 定义初始猜测
x0 = 0.5;
% 容忍度
tol = 1e-6;
% 最大迭代次数
maxIter = 1000;
% 当前猜测
x = x0;
for i = 1:maxIter
% 计算函数值和导数值
fx = cos(x) - x^3;
dfx = -sin(x) - 3*x^2;
% 更新猜测之前存储当前值作为上一次的猜测
x_prev = x;
% 更新猜测
x = x - fx / dfx;
% 检查收敛,这次是基于新旧值的差异
if abs(x - x_prev) < tol
fprintf('Found solution after %d iterations: x = %f\n', i, x);
return;
end
end
fprintf('Solution did not converge after %d iterations. Last approximation was x = %f\n', maxIter, x);
end
这段代码定义了一个名为newtonMethodExample的函数,它实现了牛顿法来找到给定方程的根。函数开始于一个初始猜测(
x
0
=
0.5
x_0=0.5
x0=0.5),并在满足容忍度条件或达到最大迭代次数时停止迭代。每次迭代计算当前点的函数值和导数值,然后根据牛顿法的公式更新猜测。
要运行这个函数,只需要在MATLAB的命令行窗口调用函数,它将执行迭代过程,并输出找到的解和迭代次数。
代码的运行结果为:

可得经过6次迭代后,我们找到了方程
f
(
x
)
=
c
o
s
(
x
)
−
x
3
f(x)=cos(x)-x^3
f(x)=cos(x)−x3 的一个根,其值约为 0.865474。这个例子展示了牛顿法在求解更复杂的非线性方程中的应用,以及它快速收敛到解的能力。

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献3条内容
已为社区贡献3条内容





所有评论(0)