带时间窗的取送货问题(Pickup and Delivery Problem with Time Windows)
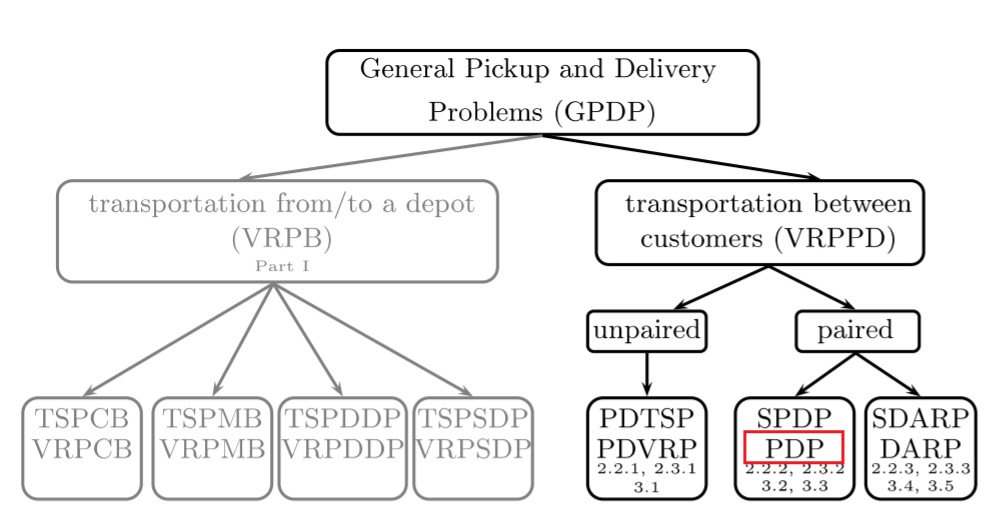
广义取送货问题(General Pickup and Delivery Problems,GPDP)可以分为两类:Backhauls,VRPB:从配送中心(depot)取货运输货物到客户点,再从客户点取货运输至配送中心交付(backhoul)。,VRPPD:货物在取货点和送货点之间流转。
取送货问题及其变体
广义取送货问题(General Pickup and Delivery Problems,GPDP)可以分为两类:
-
Vehicle Routing Problems with Backhauls,VRPB:从配送中心(depot)取货运输货物到客户点,再从客户点取货运输至配送中心交付(backhoul)。
transportation of goods from the depot to linehaul customers and from backhaul customers to the depot -
Vehicle Routing Problems with Pickups and Deliveries,VRPPD:货物在取货点和送货点之间流转。按照取货点和交货点是否是成对的,可以进一步分为两类:
- unpaired:对于货物,从某一取货点取货,可以交付至任意送货点。如果只有一辆车,那么问题简化为Pickup and Delivery Traveling Salesman Problem,PDTSP。如果是多辆车,Pickup and Delivery Vehicle Routing Problem,PDVRP。
- paired:对于某一订单,从某一指定取货点取货,只能交付至指定的送货点。如果研究的对象是货物,则有Single Pickup and Deleivery Problem,SPDP(一辆车)和PDP两个问题。如果研究的对象是乘客,则有e Dial-A-Ride Problem,DARP问题,对于一辆车的情况为the single vehicle case of the DARP as SDARP.
本文研究的取送货问题为PDP,如图:

接下来,本文所说的取送货问题,均为同车型,多辆车的Pickup and Delivery Problem,Homogeneous Multi vehicle pickup and delivery problem用PDP表示。
取送货问题数学模型(Homogeneous Multi vehicle pickup and delivery problem formulations)
每一个取货点的货量都可以满足其对应交货点的需求(因为每个取货点都关联一个交货点,因此
n
=
n
~
n=\tilde n
n=n~)
参数
- n n n:取货点数量。
- n ~ \tilde{n} n~:送货点数量,因为这里是Paired PDP问题,故 n = n ~ n=\tilde{n} n=n~。
- P P P:取货点集合, P = { 1 , . . . , n } P = \{1,..., n\} P={1,...,n}
- D D D:送货点集合, D = { n + 1 , . . . , n + n ~ } D = \{n +1,..., n +\tilde{n}\} D={n+1,...,n+n~}
- V V V:节点集合 V = { 0 , n + n ~ + 1 } ∪ P ∪ D V=\{0, n+\tilde n+1\} \cup P \cup D V={0,n+n~+1}∪P∪D
- A A A:边集, A = { ( i , j ) : i , j ∈ V , i ≠ n + n ~ + 1 , j ≠ 0 , i ≠ j } A=\{(i,j): i,j \in V, i \neq n+\tilde n+1, j \neq 0, i \neq j\} A={(i,j):i,j∈V,i=n+n~+1,j=0,i=j}
- K K K:车辆集合
- q i q_i qi:客户点 i i i的需求量(供应量),如果是取货点,则 q i > 0 q_i>0 qi>0;如果是送货点,则 q i < 0 q_i<0 qi<0;如果是起点0、终点 n + n ~ + 1 n +\tilde{n}+1 n+n~+1,则 q 0 = q n + n ~ + 1 = 0 q_0=q_{n +\tilde{n}+1}=0 q0=qn+n~+1=0。
- e i e_i ei:客户点 i i i允许的最早开始服务时间。
- l i l_i li:客户点 i i i允许的最晚开始服务时间。
- d i d_i di:客户点 i i i的服务时间(作业时间)。
- c i j k c_{ij}^k cijk:车辆k从点i到j的运输成本。
- t i j k t_{ij}^k tijk:车辆k从点i到j的行驶时间。
- C k C^k Ck:车辆 k k k的容量。
- T k T^k Tk:车辆 k k k作业时间上限(maximum route duration of vehicle/route k)
决策变量
- x i j k x_{ijk} xijk:车辆路径决策变量, x i j k = 1 x_{ijk}=1 xijk=1,车辆 k k k经过弧 ( i , j ) (i,j) (i,j);
- Q i k Q_{i}^{k} Qik:车辆 k k k离开节点 i i i时的装载量;
- B i k B_{i}^{k} Bik:车辆 k k k服务 i i i点的开始时刻;
混合整数规划模型
min
∑
k
∈
K
∑
(
i
,
j
)
∈
A
c
i
j
k
x
i
j
k
subject to.
∑
k
∈
K
∑
j
:
(
i
,
j
)
∈
A
x
i
j
k
=
1
∀
i
∈
P
∪
D
,
∑
j
:
(
0
,
j
)
∈
A
x
0
j
k
=
1
∀
k
∈
K
,
∑
i
:
(
i
,
n
+
n
~
+
1
)
∈
A
x
i
,
n
+
n
~
+
1
k
=
1
∀
k
∈
K
,
∑
i
:
(
i
,
j
)
∈
A
x
i
j
k
−
∑
i
:
(
j
,
i
)
∈
A
x
j
i
k
=
0
∀
j
∈
P
∪
D
,
k
∈
K
,
x
i
j
k
=
1
⇒
B
j
k
≥
B
i
k
+
d
i
+
t
i
j
k
∀
(
i
,
j
)
∈
A
,
k
∈
K
,
x
i
j
k
=
1
⇒
Q
j
k
=
Q
i
k
+
q
j
∀
(
i
,
j
)
∈
A
,
k
∈
K
,
max
{
0
,
q
i
}
≤
Q
i
k
≤
min
{
C
k
,
C
k
+
q
i
}
∀
i
∈
V
,
k
∈
K
,
∑
j
:
(
i
,
j
)
∈
A
x
i
j
k
−
∑
j
:
(
n
+
i
,
j
)
∈
A
x
n
+
i
,
j
k
=
0
∀
i
∈
P
,
k
∈
K
B
i
k
≤
B
n
+
i
k
∀
i
∈
P
,
k
∈
K
.
∀
i
∈
V
,
k
∈
K
,
e
i
≤
B
i
k
≤
l
i
∀
i
∈
V
,
k
∈
K
,
B
n
+
n
~
+
1
k
−
B
0
k
≤
T
k
∀
k
∈
K
,
x
i
j
k
∈
{
0
,
1
}
∀
(
i
,
j
)
∈
A
,
k
∈
K
\begin{align} \min \quad & \sum_{k\in K}\sum_{(i,j) \in A} c_{ij}^k x_{ij}^k \\ \text{subject to.} \quad &\sum_{k \in K} \sum_{j:(i, j) \in A} x_{i j}^{k} =1 & \forall i \in P \cup D, \\ &\sum_{j:(0, j) \in A} x_{0 j}^{k}=1 & \forall k \in K, \\ &\sum_{i:(i, n+\tilde{n}+1) \in A} x_{i, n+\tilde{n}+1}^{k} =1 & \forall k \in K, \\ &\sum_{i:(i, j) \in A} x_{i j}^{k}-\sum_{i:(j, i) \in A} x_{j i}^{k} =0 &\forall j \in P \cup D, k \in K, \\ &x_{i j}^{k}=1 \Rightarrow B_{j}^{k} \geq B_{i}^{k}+d_{i}+t_{i j}^{k} & \forall(i, j) \in A, k \in K, \\ &x_{i j}^{k}=1 \Rightarrow Q_{j}^{k} =Q_{i}^{k}+q_{j} & \forall(i, j) \in A, k \in K, \\ &\max \left\{0, q_{i}\right\} \leq Q_{i}^{k} \leq \min \left\{C^{k}, C^{k}+q_{i}\right\} & \forall i \in V, k \in K, \\ & \sum_{j:(i, j) \in A} x_{i j}^{k}-\sum_{j:(n+i, j) \in A} x_{n+i, j}^{k}=0 &\quad \forall i \in P, k \in K\\ & B_{i}^{k} \leq B_{n+i}^{k} \quad \forall i \in P, k \in K . & \forall i \in V, k \in K,\\ & e_i \leq B_i^k \leq l_i & \forall i \in V, k \in K,\\ & B_{n+\tilde{n}+1}^k -B_{0}^k \leq T^k &\forall k \in K,\\ &x_{i j}^{k} \in\{0,1\} & \forall(i, j) \in A, k \in K \\ \end{align}
minsubject to.k∈K∑(i,j)∈A∑cijkxijkk∈K∑j:(i,j)∈A∑xijk=1j:(0,j)∈A∑x0jk=1i:(i,n+n~+1)∈A∑xi,n+n~+1k=1i:(i,j)∈A∑xijk−i:(j,i)∈A∑xjik=0xijk=1⇒Bjk≥Bik+di+tijkxijk=1⇒Qjk=Qik+qjmax{0,qi}≤Qik≤min{Ck,Ck+qi}j:(i,j)∈A∑xijk−j:(n+i,j)∈A∑xn+i,jk=0Bik≤Bn+ik∀i∈P,k∈K.ei≤Bik≤liBn+n~+1k−B0k≤Tkxijk∈{0,1}∀i∈P∪D,∀k∈K,∀k∈K,∀j∈P∪D,k∈K,∀(i,j)∈A,k∈K,∀(i,j)∈A,k∈K,∀i∈V,k∈K,∀i∈P,k∈K∀i∈V,k∈K,∀i∈V,k∈K,∀k∈K,∀(i,j)∈A,k∈K
- 目标函数(1)最小化总体行驶成本;
- 约束(2)保证了每个客户点都被访问了一次;
- 约束(3-5)分别保证了每辆车必须从始发站出发,到达并离开每个客户点,并最终回到终点站;约束(5)为Flow conservation
- 约束(6)消除子回路。
- 约束(7-8)车辆容量约束
- 约束(9),联结约束(coupling constraint),同一需求的起点和终点都必须是同一辆车提供服务
- 约束(10),优先级约束(precedence constraint),针对每一货运需求,取货任务的服务顺序须于送货任务前。
- 约束(11)时间窗约束
- 约束(12)路径时长限制
【注】约束(6)和(7)是非线性的,可以用大M进行线性化
参考:
- Parragh S N, Doerner K F, Hartl R F. A survey on pickup and delivery problems: Part II: Transportation between pickup and delivery locations[J/OL]. Journal für Betriebswirtschaft, 2008, 58(2): 81-117. https://doi.org/10.1007/s11301-008-0036-4.

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献16条内容
已为社区贡献16条内容





所有评论(0)