介绍恒压频比的开环控制方法驱动永磁同步电机的转动，首先分析恒压频比的控制原理：恒压频比的控制方法是一种常用的开环控制策略，它通过调节电机定子电压和频率的比例来保持电机磁场的恒定。在这种控制方法中，控制器根据电机的转速和负载情况，实时调整定子电压和频率，以确保电机在稳定范围内运行。通过调节恒压频比，可以控制电机的转速和负载，从而实现精确的控制和调节。这种控制方法具有简单、易于实现和鲁棒性强的特点，因此在永磁同步电机的转动控制中得到了广泛的应用。

在Matlab/Simulink中的仿真分析：为了验证恒压频比开环控制方法的可行性，我们可以在Matlab/Simulink中建立相应的仿真模型。在仿真模型中，我们可以设置电机的参数、负载情况、转速要求等，然后模拟恒压频比控制器的工作过程，观察电机的转速和负载变化情况。

通过仿真分析，我们可以验证恒压频比控制方法的准确性和稳定性，为后续的工程实现提供理论支持。

一、 恒压频比（V/F）控制原理

变频调速系统在电机控制中扮演着重要角色。为了确保电机的优良调速性能，我们需要深入理解变频过程中的电机气隙磁通变化。变频调速系统通过改变电机定子上的电源频率来调整电机的转速。在变频过程中，电机气隙磁通的变化是一个关键因素。气隙磁通的大小和形状直接影响电机的电磁性能和机械特性。为了保持电机气隙磁通为最大值，我们需要对变频控制系统进行精确调整。这可以通过控制电源频率、电压和电流来实现。通过优化这些参数，我们可以在允许的电流下获得最大转矩，从而提高电机的调速性能。交流电机每相定子感应电动势为:

式中4.44Nk是由电动机结构决定的常数。从上式可以看出，在改变频率时要保持气息磁通。不变，就需要同时改变E，使E,随变化并保持E。1为固定的常数C。因为E,不能直接检测和控制，在忽略定子绕组电阻时E,近似等于电动机端电压U,，而U,和,都可方便地通过变频器控制，因此变频调速系统保持U./,为常数的控制就称为恒压频比控制(VF)。恒压频比开环控制框图如下所示：

永磁同步电机和异步电机在恒压频比控制方法上确实存在相似之处。这种控制方法通过调整电机的输入电压和频率，使气隙磁通保持恒定，从而实现电机的稳定运行。然而，需要注意的是，这种控制方法并没有引入电机电流、电压、位置等物理量的反馈机制。因此，在实际应用中，其动态性能可能相对较差。在给定目标转速发生变化或者负载突变的情况下，电机可能会出现失步和震荡的问题，但该控制方法胜在简单，多适用于对转速精度要求不高的场合。

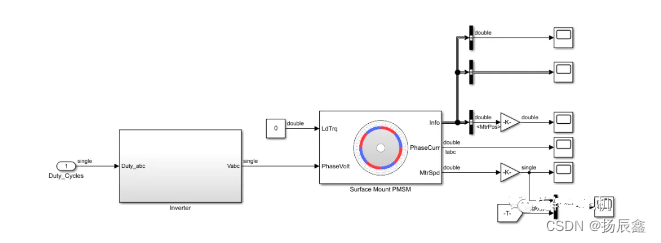
永磁同步电机恒压频比开环控制系统Matlab/Simulink仿真框图如下：

二、仿真电路分析

2.1.1.恒压频比控制算法

恒压频比控制算法：永磁同步电机转速与频率的换算关系如下所示：

首先，将设定的电机目标转速通过上式换算为频率，由于该开环控制系统没有自动限制启动电流的作用，因此加入了一个斜坡函数使频率有一个平缓的变化过程。例如仿真中设定的目标转速为1200r/min，换算为频率的过程如下图所示：

然后，由恒压频比V/F控制算法特性（下图所示），使输入电压与频率同步变化，从而保持气隙磁通恒定。低频时Us和Eg都较小，定子电阻和漏感压降所占分量比较显著，不能再忽略，此时人为的把定子电压抬高一些，近似的补偿定子阻抗压降，如下图b线所示：

由上图可知输入电压与频率的关系为（带低频补偿的b线，已知（0，U0）（f1N，UsN））：

将频率通过上式换算为电压，由电机的额定转速计算出额定频率f1N（永磁同步电机转速与频率的关系）。永磁同步电机的恒压频比控制为基频以下调速，系统最高频率不能超过额定频率f1N，例如仿真中所选永磁同步电机的额定转速为12540r/min，计算出额定频率f1N为1463Hz，为系统最高设定频率。

目标转速设置为1200r/min，将转速换算为频率，再由频率的变化得到输入电压的变化，如下图所示：

此处作了一个归一化处理，将电压的变化除以电机额定电压，使输出电压的范围落在[0,1]区间内。

将频率转换为角速度，再对角速度求积分获得当前的角度，如下图所示：

此时已获得输入电压的幅值Um与相角wt，再通过下式将幅值与相角的电压表示转化为两相αβ坐标系下的电压表示：

αβ坐标系下的电压表示为：

接着采用反Clark变换，得到最终输入到电机的三相电压：

2.1.2.输出处理

 对恒压频比控制算法的输出电压做处理，使其落在[0,1]的范围内：

2.1.3.主电路

主电路包括逆变电路与永磁同步电机，逆变电路如下图所示，采用Average-Value Inverter模块直接生成三相正弦电压，下图为目标转速1200r/min下输入到电机的电压波形。

2.2.仿真结果分析

2.2.1.设定目标转速为1200r/min

目标转速与实际转速的波形曲线：

稳态时，目标转速与实际转速的误差：

稳态时，电机定子电流：

电机转子位置：

 dq坐标系下的定子电流值：

电磁转矩：

2.2.1.设定目标转速为变化值

目标转速：

目标转速与实际转速：

 从图中可以看出电机加减速有一段斜坡时间，电机加减速的快慢由恒压频比控制算法中由转速换算为频率时所设置的斜坡函数斜率有关。

总结

永磁同步电机和异步电机在恒压频比控制方法上确实存在相似之处。这种控制方法通过调整电机的输入电压和频率，使气隙磁通保持恒定，从而实现电机的稳定运行。

然而，需要注意的是，这种控制方法并没有引入电机电流、电压、位置等物理量的反馈机制。因此，在实际应用中，其动态性能可能相对较差。在给定目标转速发生变化或者负载突变的情况下，电机可能会出现失步和震荡的问题。

为了解决这个问题，可以在控制系统中加入电机电流、电压、位置等物理量的反馈机制。这样，控制系统就可以根据这些物理量的变化来调整电机的输入电压和频率，从而改善电机的动态性能。同时，还可以引入一些先进的控制算法，如模糊控制、神经网络控制等，来提高控制系统的性能和稳定性。