4. 分析：完整规范

本节概述了网络分析概念的更正式规范，在此基础上构建了 sDNA 积分、可达性地图、测地线、网络半径和凸包。

请注意，从sDNA版本3开始，该规范中的一些已经改变，特别是拆分连线的处理（其基本原理在博客文章中解释）。版本 1 和 2 的规范仍然可用。

4.1. 定义

连线【link】

跨越两个连接点或连接点和端点之间的间隙的一条或多条折线。

SDNA 接受链接节点格式的数据(尽管严格来说，节点是不必要的)。它还接受折线节点格式的数据。请注意，我们在链接和折线之间做了区分: 这些格式的一些用户没有这样做，而且将把它们视为同一件事情。这对于理解 sDNA 很重要，但是在使用软件时并不重要，因为它可以接受任何一种格式。

为了表示运输网络，折线可以以道路或路径中心线为中心。波形线也可以用来勾勒出行人路线和人行横道，从而形成一个行人中心线网络。据我们所知，迄今为止最大的一座长达1400公里，是为 Yvelines 的圣昆廷集聚区而建造的。

多线段【Polyline】

一个链接由一条或多条折线组成。这与多边形的 GIS 或 CAD 概念相匹配: 作为单个单元处理的连续的线段链，通常带有许多附加的数据字段。折线的长度、角度(直接性/弯曲度)、连接性(折线的其他端点的数量)都有所不同。

在 sDNA 内部，折线被视为不可分割的起源; 所有源自折线的流被视为源自其中间(根据距离度量定义为欧几里得或角中心)。作为目的地，折线在离散空间模式下被视为不可整数，或在连续空间模式下被视为可整数。

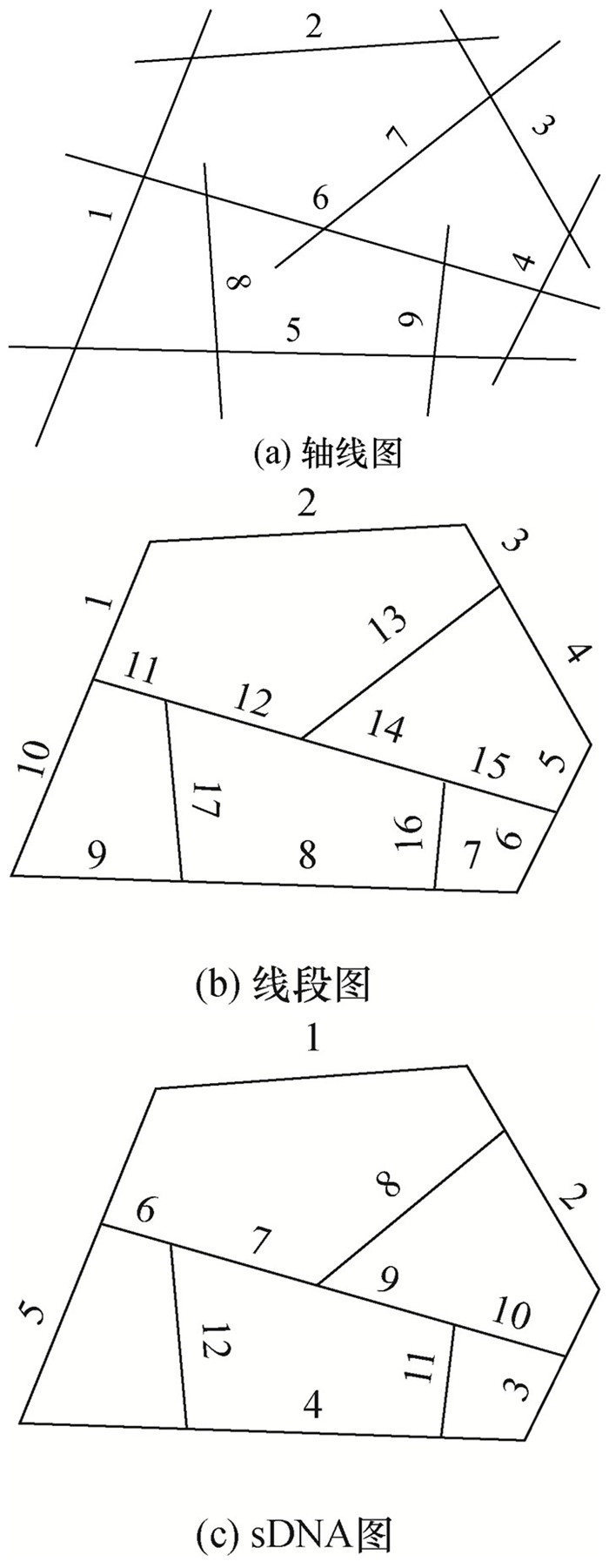
【注释】sDNA与传统空间句法对于线段的不同定义

交叉点（junction）

至少连接 3 个连线末端的点。

距离公制【Distance Metric】

度量是一个函数，用来定义网络上的点之间是“接近”还是“远离”对方的意义。SDNA 目前支持

• 欧氏度量
  在网络中定义的距离单位中沿网络测量的距离。这是日常生活中关于距离的概念
• 角度
  以角度变化量度的距离，即连杆上的转角和连接处的转弯
• 定制公制
  测量距离根据用户选择的数据字段定义在多线
• 混合公制
  根据用户定义的公式测量的距离，该公式可以基于欧几里得度量、角距离、身高增益和损失以及自定义数据
• 其他指标
  我们提供了一些具体的指标，适合于城市网络分析(车辆，行人，自行车)

半径【Radius】

分析是从用户定义的半径内的每个原点执行的，半径以数据的空间单位表示。通常，原点集等于折线集，因此围绕每条折线进行分析。 用户通常希望以米为单位表示半径，因此在使用sDNA之前，必须注意将空间数据投影到以米为单位的坐标系中。半径可以理解为可变的浮动集水区、分析位置或最大行程距离。 存在两种处理半径边界的模式：

离散空间 【Discrete space】
当且仅当折线的中心落在半径内时，所有折线都包含在每个原点的半径中 连续空间折线将动态分割，并且只有那些正好落在每个原点半径内的部分才会包含在该原点的分析中。分数折线的权重根据其表示的链接长度的分数向下调整。

连续空间【Continuous space】
比离散空间需要的计算量略多，但建议用于半径与最长折线具有相同（或更小）数量级的分析。这通常意味着小规模分析，例如行人或骑自行车者网络。

默认情况下，半径表示为欧氏距离，但可以在离散空间模式下设置其他径向度量（角度、自定义、混合等）。如果使用带状半径，则每个半径将排除下一个最小半径的链接。

测地线【Geodesic】

根据给定的距离度量，测地线是网络上两点之间的最短路径。

存在各种特殊情况，严格来说这是不正确的。注意，当使用非欧几里德度量时，网络半径可能比测地线短。由于网络半径要求具体分析的局部性，我们约束这样的测地线只使用半径内的网络。可以在高级配置和命令行选项中修改此行为。处理这些边缘案例的含义在[1]中进行了探讨。
[1]Cooper （2015） 接近性和中介性度量的空间定位：一种自相矛盾但有用的网络分析形式. 国际地理信息科学杂志29（8）http://www.tandfonline.com/doi/abs/10.1080/13658816.2015.1018834

4.2.加权【Weighting】

通过加权来确定分析中每个起点和终点的重要性。权重可以是

• 每个多段线
• 每个链接
• 每个单位长度。

所有这些都可以基于自定义数据。如果未给定权重，则所有权重都将默认为1，尽管此默认值可以按多段线、链接或单位长度进行解释（如上所述）。

权重的选择应该反映出您认为是分析中网络数量的最佳衡量标准：链接数量、长度或自定义属性（如人口加工作数量或地址点数量）。如果你没有实际的人口普查数据，城市网络的推荐选择是链接数量。这是因为链路密度随着工作岗位和人口数量的增加而增加：因此，通过链路数量来测量网络在一定程度上有助于通过网络几何结构捕捉这些其他变量。

加权	输出后缀	出发地/目的地重量字段	结果
链接		留空	所有起点和终点链路的权重均为 1。建议默认用于不带重量数据的分析
长度	Wl	留空	所有起点和终点链接的权重都等于它们的长度。长度比链接计数更能代表城市密度的情况的替代默认值
多段线	Wp	留空	所有折线的权重均为 1（不推荐，我们不知道这样做的逻辑用途）
链接		指定用户权重数据	所有起点和目的地链接的权重等于用户定义字段提供的自定义权重（或由多段线表示的链接的平均值）。建议用于根据土地利用数据附加权重
长度	Wl	指定用户权重数据	所有起点和目的地链接的权重等于用户定义字段提供的自定义权重（或由多段线表示的链接的平均值）。建议用于根据土地利用数据附加权重
长度	Wp	指定用户权重数据	所有折线的权重都等于自定义权重。建议用于在子链路级别附加地址点或人口普查数据

请注意，地址点(附加到单个建筑物)可以通过使用 GIS 空间连接来处理，从点数据到网络传输诸如楼面面积等数据。如果子链接精度是必要的，链接应分裂成多个子链接。

4.3 处理单向系统【Handling of one-way systems】

在计算测地线时，分析考虑了指定的单向和垂直单向连接。然而，当计算单个链接对其自身的接近度/间距/半径重量等的贡献时，假设链接上的所有点都可以直接从彼此到达，而不考虑单向状态。这是为了保持与原点近似和链接中心的选择以及在 sDNA 内处理其他微模型情况的一致性。在没有黑洞/白洞的情况下(单向系统中的点不可能逃脱/进入) ，这将导致所有足够大半径的链接/长度/重量的正确计算(也就是说，如果半径超过了从任何链接到单向系统本身的最大测地线)。起源的自我封闭/自我介于两者之间通常对整体分析只有很小的贡献，主要是为了一致性。

4.4 输出结果的数学定义【Mathematical definition of outputs】

4.4.1 记号

在以下各节中，

• 全球空间系统中的折线集表示为 N【The set of polylines in the global spatial system is denoted N】
• 从链接 x 开始的网络半径中的折线集表示为 Rx【The set of polylines in the network radius from link x is denoted Rx】
• 半径内任何折线 y 的比例表示为 P（y）。在离散空间分析中，这总是等于 0 或 1，即 y∈Rx⇔P（y）=1。在连续空间中，0≤P（y）≤1【The proportion of any polyline y within the radius is denoted P(y). In discrete space analysis, this always equals 0 or 1, i.e. y∈Rx⇔P(y)=1. In continuous space, 0≤P(y)≤1】
• Length of a polyline y is denoted L(y)【折线 y 的长度表示为 L（y）】
• The distance according to a metric M, along a geodesic defined by M, between an origin polyline x and a destination polyline y is denoted dM(x,y)【根据度量 M 沿 M 定义的测地线，在原点折线 x 和目标折线 y 之间的距离表示为 dM（x，y）】
• 【在原点折线 x 和目标折线 y 之间沿度量 M 定义的测地线的网络欧几里得距离表示为 dEM（x，y）】【The network Euclidean distance along a geodesic defined by a metric M, between an origin polyline x and a destination polyline y is denoted dEM(x,y)】
• 【折线 y 的权重表示为 W（y）】【Weight of a polyline y is denoted W(y)】

W(y) is computed differently according to the weighting scheme. If 【W（y） 根据加权方案以不同的方式计算。如果】

【其中 L（Z） 是由一条或多条多段线 P 组成的链接 Z 的长度，使得 y∈P】【where L(Z) is the length of the link Z formed of one or more polylines P such that y∈P】
.

4.4.2 中心性度量【Centrality measures】

远离度or距离中心性

根据所选的距离度量，远距离测量为平均角度、欧几里得、自定义或混合距离。它分别缩写为MAD，MED，MCD和MHD。

请注意，平均而言，同一链路内两个任意点之间的遍历距离是遍历整个链路的距离的1/3。原点链接对其自身远距离的贡献以这种方式包括在内。

邻近度or接近中心性【Closeness】

sDNA不是衡量邻近度，而是衡量距离度，这告诉你完全一样的事情，以不同的方式。文献通常将邻近度定义为1/距离度，尽管这是一个指数分布，因此在统计上更难处理。另一个不受这个问题影响的邻近度定义是距离。我们不倾向于使用任何一种，更倾向于使用Farness【距离度】或NQPD用于相同的目的。

【注释】
sDNA模型中的接近度指标与交通可达性(accessibility)相似，用于衡量给定半径内其他路段的接近难易程度。接近度是用路段权重与相邻路段距离之比的期望值来衡量的，即考虑距离作为惩罚因素的网络平均权重(network quantity penalized by distance，NQPD)，表示如下[21]：

式中：x为待计算的路段；Rx为从路段x出发，在给定半径R内可达的其他路段集合；W(y)为路段y的权重，可表示路段长度或兴趣点数量等；d(x, y)为路段x和y之间的距离，包括Euclid距离或角度距离等；P(y)表示路段y在Rx中的比例。离散空间中，P(y)=1, y∈Rx; P(y)=0, y∉Rx；连续空间中，P(y)为路段y在半径R内部分的长度占比。

平均测地线长度

平均测地线长度（MeanGeoLen 或 MGL）是半径（由所选度量定义）内所有测地线的平均长度（始终采用欧几里得度量）。

MGL 可用作固定度量，以比较来自不同混合指标的测地线。例如，可以通过计算将考虑道路交通的骑车人指标与没有机动车交通量的骑车人指标进行比较：

这将显示骑自行车的人必须绕大弯以避开机动车交通的区域。

距离作为惩罚因素的网络平均权重（重力模型）

NQPD 是一种接近形式，通常称为重力模型，它考虑了网络权重的数量和可访问性。相比之下，Farness【距离度】只考虑可访问性，而权重只考虑重量。

请注意，平均而言，在同一链路内的两个任意点之间遍历的距离是遍历整个链路的距离的1/3。包含原始链接对其自身NQPD的贡献。

nqpdn和nqpdd默认为1，但可以在高级配置中设置为其他值（它们分别代表NQPD分子和分母）。对于任何给定的应用程序，问题在于确定每个应用程序的正确值，即网络数量和可访问性的相对重要性。为了回答这个问题，我们建议使用基于Farness和Weight的多元translog线性回归来近似NQPD，即使用模型

一旦获得了合适的β值，这些值就可以应用于nqpdn≈β2和nqpdd≈-β1。

穿行度or中介中心性【Betweenness】

中介性计算通过顶点的测地线路径的数量，即顶点位于其他顶点对之间的最短路径上的次数。


论文图片来源：http://jst.tsinghuajournals.com/article/2022/4316/1655364495894-882026326.htm

注意，测地线的端点是y和z，而不是测量介数的x。1/2对OD（y，z，x）的贡献反映了测地线的末端链路，测地线的穿越频率平均是链路中心旅程开始和结束频率的一半。1/3的贡献表示原点自介性。

请注意，在原点和目的地对之间存在多条等长测地线的情况下，sDNA将只考虑发现的第一条此类测地线。这与一些文献中介数分布在所有等长测地线上的情况不同。如果这是值得关注的（例如，分析完美的网格模式），我们建议使用混合度量在分析中添加少量随机性，并在必要时将这种方法与过采样相结合。（通常不需要过采样，因为每个原点都会重新应用随机性；即，即使没有过采样，分析的每个链接也代表随机分布的不同样本）。可以在高级配置和命令行选项中设置随机性和过采样。

双相中介度【Two phase betweenness】

双相中介性（TPBt） 表示中介性，但不是按原产地和目的地权重的乘积加权，而是按目的地权重分布。自从实现这一点以来，我意识到它代表了来自一些旧文献中称为可访问性的哈夫模型的流程。因此，它是通过链接 x 的测地线的总和，由测地线原点 y 可访问的网络数量的比例加权，该比例由测地线目的地 z 表示。

其中，总权重（y）是以每个y为半径的总权重。

两相目的地

两相目的地 （TPD） 测量两相中介度模型中每个目的地收到的原点权重比例。它类似于两步浮动集水区和哈夫可达性模型。

在正常的中介分析中，此量等同于权重，但由于每个原点的测地线权重在两阶段模型中受到限制，因此沿测地线传输到目的地的权重不仅取决于目的地半径内的权重，还取决于目的地与之竞争的内容。因此，与下面描述的链接、长度和权重度量相比，此度量对空间层次结构的区分性更强。

请注意，TPBt 具有网络数量的单位，并随网络数量缩放，而不是像标准中介性那样的网络数量的平方。因此，它对应于具有行程生成和分配阶段的运输模型，而正常中介关系可以被视为机会模型。

网络绕行分析【Network detour analysis】

网络绕行分析将直线距离与实际网络距离进行比较，回答“网络偏离最直接路径的程度？

平均乌鸦飞行【Mean Crow Flight】

乌鸦平均飞行 （MCF） 是每个原点与半径内所有链接之间的乌鸦飞行距离的平均值。

其中CFD（x，y）是x和y中心之间的乌鸦飞行距离。
MCF可以与平均测地长度（MGL）进行比较；也就是说，MGL/MCF给出了测地线必须偏离期望线的程度的度量。

导流比导流比（Div）是半径内所有链路测地线长度与乌鸦飞行距离的平均比。它与MGLMCF的不同之处在于，在取平均值之前单独计算比率。

4.4.3 网络形状分析【Network shape analysis】

网络形状分析是指网络在半径范围内的整体空间足迹的形式。这可以用于计算效率的度量，例如，凸壳面积/长度提供了每单位网络长度的欧几里得空间覆盖率的度量。

以下所有度量都基于网络半径内所有点的二维凸包。对于三维网络，在计算凸包之前，将网络投影到x-y平面上。

凸壳面积

凸壳面积(HullA)是凸壳在半径内被网络覆盖的面积。

凸壳周长

凸壳周长(HullP)是凸壳在半径范围内被网络覆盖的周长。

凸壳最大半径

凸壳最大半径(HullR)是从起点到凸壳最大半径(如乌鸦飞行)的距离。换句话说，它是到网络半径内任何点的最大乌鸦飞行距离，因此代表了从原点可以到达的单一路线，可以像乌鸦飞行那样覆盖最远的距离。

凸壳轴承

这是凸壳最大半径的罗盘方位，从投影网格的正 y 方向测量(这通常是网格的北方)。

凸壳形状指数

这被定义为

4.4.4 半径描述测量值

对于每个原点的每个半径，给出了以下措施：

连线

连线【Links】（Lnk）是半径内的链路数，∑y∈RxP（y）

长度

长度【Length】（Len）Lengt是半径内的网络总长度，∑y∈RxL（y）P（y）

权重

权重（Wt）是半径内的总权重，∑y∈RxW（y）P（y）。如果您希望规范化网络数量的任何其他输出度量，这是最好的控件，因为它适合于适当的分析类型。

角距离

角距离（Ang-Dist或AngD）是半径∑y∈Rxdθ（yR）内所有链路上的总角曲率，其中yR是y仅在半径内的比例。

交叉点

交叉点（Jnc）统计半径中的连接数。请注意，只计算连接之间的连接，而不计算多段线。

连通性or可达性

连通性（Con）是半径中的总连通性：每个连接点连接的链路末端数量之和。请注意，在这种衡量标准中，单向街道算作半个连接端（与LConn不同，在LConn中，它们被完全计算在内）。

4.4.5 单个折线描述度量

线段长度

直线长度（LLen）是多段线的欧几里得长度，L（y）。
线路连接线路连接（LConn）是指该线路所连接的其他线路端的数量。也称为度中心性。

线段角曲率

直线角曲率（LAC）是沿直线全长的累积角曲率，单位为度：dθ（y）。

连线混合度量

在混合分析中，给出了折线的混合度量：混合度量正向（HMf）和混合度量反向（HMb）。由于高度增加或与通行方向相关的自定义行为，例如自动扶梯、交通优先级或单程通行费，每个方向的指标可能不同。

连线弯曲度

直线正弦度（LSin）是乌鸦在其端点之间飞行时的直线长度除以距离。类似于导流比，但仅适用于单线。

连线方位角

直线方位（LBear）是直线端点之间的指南针方位，从投影栅格的正y方向测量（通常为栅格北）。

连线分数

链接分数（LFrac）是这条线所代表的链接的比例，P（y）。

4.5. 输出和缩写列表

缩写	说明
AngD	Angular Distance in Radius半径角距离
BtA	Betweenness Angular中介角度
BtC	Betweenness Custom中介性定制
BtE	Betweenness Euclidean欧几里得的中介性
BtH	Betweenness Hybrid中介混合
Conn	Connectivity in Radius半径内的连通性
DivA	Diversion Ratio in Radius Angular半径角中的导流比
DivC	Diversion Ratio in Radius Custom半径自定义中的导流比
DivE	Diversion Ratio in Radius Euclidean半径欧几里得的导流比
DivH	Diversion Ratio in Radius Hybrid半径混合中的导流比
HMb	Line Hybrid Metric (backwards direction)线混合指标（向后方向）
HMf	Line Hybrid Metric (forwards direction)线混合指标（向前方向）
HullA	Convex Hull Area凸壳面积
HullB	Convex Hull Bearing of Maximum Radius最大半径凸壳轴承
HullP	Convex Hull Perimeter凸壳周长
HullR	Convex Hull Maximum (Crow Flight) Radius凸壳最大(乌鸦飞行)半径
HullSI	Convex Hull Shape Index凸壳形状指数
Jnc	Junctions in Radius半径中的交叉点
LAC	Line Angular Curvature直线角曲率
LBear	Line Bearing线轴承
LConn	Line Connectivity线路连接度
Len	Length in Radius半径长度
Lfrac	Link fraction (for current line)链路分数(当前线路)
LLen	Line Length线路长度
Lnk	Links in Radius半径中的链接
LSin	Line Sinuosity线路弯曲
MAD	Mean Angular Distance in Radius半径的平均角距离
MCD	Mean Custom Distance in Radius半径平均自定义距离
MCF	Mean Crow Flight Distance in Radius半径内平均乌鸦飞行距离
MED	Mean Euclidean Distance in Radius半径的平均欧几里得度量
MGLA	Mean Geodesic Length in Radius Angular半径角的平均测地长度
MGLC	Mean Geodesic Length in Radius Custom半径自定义的平均测地长度
MGLE	Mean Geodesic Length in Radius Euclidean欧氏半径中的平均测地长度
MGLH	Mean Geodesic Length in Radius Hybrid半径混合的平均测地长度
MHD	Mean Hybrid Distance in Radius半径平均混合距离
NQPDA	Network Quantity Penalized by Distance in Radius Angular半径角距离惩罚网络量
NQPDC	Network Quantity Penalized by Distance in Radius Custom半径定制中网络量的距离惩罚
NQPDE	Network Quantity Penalized by Distance in Radius Euclidean欧氏半径中由距离惩罚的网络量
NQPDH	Network Quantity Penalized by Distance in Radius Hybrid半径混合动力中网络量的距离惩罚
SAD	Sum of Angular Distance in Radius *半径内的角距离总和 *
SCD	Sum of Custom Distance in Radius *半径自定义距离之和 *
SCF	Sum of Crow Flight Distance in Radius *半径内乌鸦飞行距离之和 *
SED	Sum of Euclidean Distance in Radius *半径内的欧几里得度量总和 *
SGLA	Sum of Geodesic Length in Radius Angular *测地长度在半径角中的和
SGLC	Sum of Geodesic Length in Radius Custom *半径自定义测地长度之和 *
SGLE	Sum of Geodesic Length in Radius Euclidean *欧氏半径中测地长度之和 *
SGLH	Sum of Geodesic Length in Radius Hybrid *半径杂交中测地长度之和 *
SHD	Sum of Hybrid Distance in Radius *混合半径距离之和 *
TPBtA	Two Phase Betweenness Angular两相中介性角度
TPBtC	Two Phase Betweenness Custom自定义两阶段中间性
TPBtE	Two Phase Betweenness Euclidean欧式距离两相中介性
TPBtH	Two Phase Betweenness Hybrid混合两相中介性
TPDA	Two Phase Destination Angular两相目的地角度
TPDC	Two Phase Destination Custom自定义两相目的地
TPDE	Two Phase Destination Euclidean欧式距离两相目的地
TPDH	Two Phase Destination Hybrid混合式两相目的地
Wl	Weighted by Length (as opposed to Link)按长度加权(相对于连线)
Wp	Weighted by Polyline (as opposed to Link)按多段线加权(相对于连线)
Wt	Weight in Radius半径内的权重

【sDNA公号文章内的参数度量翻译】