永磁同步电机高性能控制算法（9）—— 简单解析基于LESO的线性ADRC转速环为什么没有超调量
在往期内容中，已经公布了基于线性扩张状态观测器（LESO）的线性自抗扰（LADRC）转速环与传统PI转速环的对比。与转速环采用PI相比，基于LESO的线性ADRC转速环能够更快的达到给定转速，而且无超调量。
1.基于LESO的线性ADRC转速环与基于PI调节器的转速环的对比
在往期内容中，已经公布了基于线性扩张状态观测器（LESO）的线性自抗扰（LADRC）转速环与传统PI转速环的对比。
与转速环采用PI相比，基于LESO的线性ADRC转速环能够更快的达到给定转速，而且无超调量。
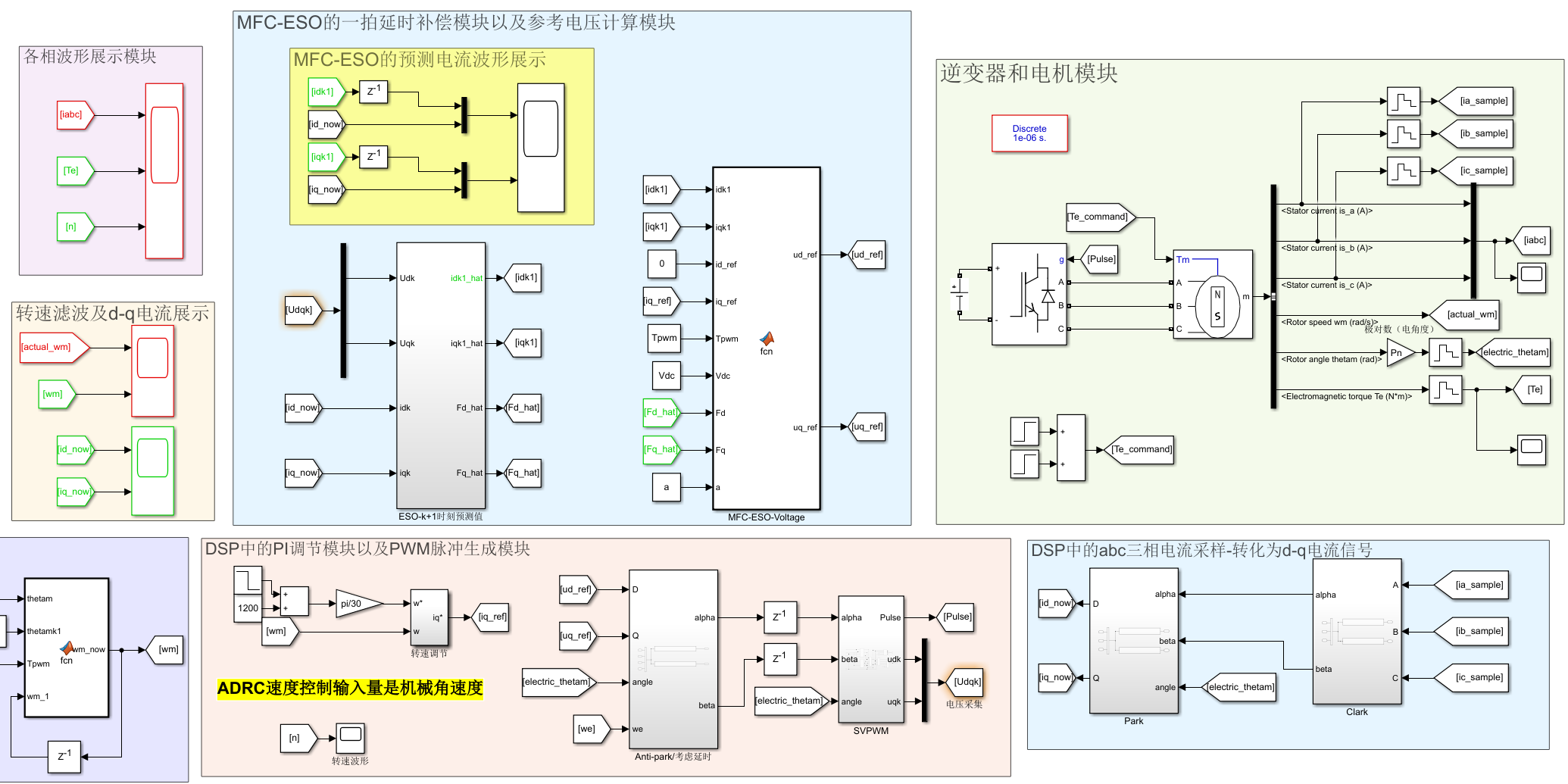
2.基于LESO的线性ADRC转速环的仿真搭建
参考文献（南航黄老师，在高性能控制方面的论文我感觉是写的很好的。论文质量要远远远远远高于那种通过靠更换观测器水出来的论文）：
这篇论文讲的是高阶LESO，不过论文中把各阶LESO的表达式都列写出来了，而且也把框图画出来了，所以我当时就是照着这篇来搭建的。
先看看电机转速方程：
然后开始构造转速方程的超局部模型，就看完下面画的方框就行了。
我为什么把这个式子叫做转速方程的超局部模型？
在之前的电流环无模型算法中，用到电流环的超局部模型表达式如下：
对比一下看看，这两个式子的等式左边都是变化率（转速的变化率以及电流的变化率），等式的右边都是一个扰动量F、一个输入量（转速环的输入量是q轴电流，电流环的输入量是电压u）以及一个输入量的增益（转速环的输入量增益为b0=Ktn/Jn=1.5*Pn*flux/Jn，电流环的输入量增益为a=1/L）。这两个式子中，只有输入量的增益与系统参数有关。转速环的输入量增益与电机极对数Pn、磁链flux、转动惯量Jn有关，电流环的输入量增益与电感有关。
那当这些参数变化的时候，基于ESO的ADRC能否还能具有鲁棒性呢？当然是能的，因为当这些参数变化的时候，相当于把参数变化带来的误差看做一个新的扰动，又被归类到扰动量F去了。但是这些参数不能变化太大，变化个一两倍的话，系统的性能还是没问题的。
LESO的公式
文章这是给了多阶的ESO公式，按照他给的这个模板，直接把n=1带入，就可以得到最低阶数的LESO公式了。文章里面的公式看不懂的话可以看看这一篇知乎：
或者直接按照之前电流环的公式来搭建（两个公式就是符号换了而已，其他没有任何区别）：
注意，把公式列写好之后，一定要离散化，一般就是用前向欧拉离散化，也还是在我电流环ESO的这篇论文里讲到了。
到这一步，我们相当于把观测器设计好了，但是还没有实行控制。
构建控制律
文章中构建的控制如下：
不要在论文中看的控制率就瞎用，我们要想为什么？我们把式子（11）带入式子（2）中可以得到如下的表达式。因为Z2就是Fw的估计量，ESO设计比较准确的话，那就会有Z2=Fw，进而将下式进一步化简。
从上式可以看的，在不考虑转速环输出饱和的话，参考转速与实际转速的差值越大或者Kp的值越大，那么电机加速度就越大，达到参考转速的时间就越短。
现在观测器有了，控制率也有了，就可以实现闭环控制了。控制框图如下，图里画的式高阶LESO，自己改成低阶的就行了。
这里值得注意的是，注意ESO中的估计值Z1、Z2、Z3、Z4，这些估计值都是通过串联积分的形式积分得到的。ESO就相当于一个积分器。
而控制率中还有一个比例环节Kp。因此，实际上的LADRC也就是等同于一个比例环节Kp+ESO（积分环节）。
对LADRC比较有兴趣的可以看看下面几篇知乎：
https://zhuanlan.zhihu.com/p/677913331
3.LADRC为什么没有转速超调量？
根据上述观测器以及控制率搭建的仿真如下：（这里还有一点要注意的是，ADRC的公式中，转速环的输入都是机械角速度，而不是转速n了，所以转速环的时候，还要把原来的比例系数Kp给换算一下。）
仿真对比如下（更详细的仿真已经放在文章开头了。下文的积分器输出对比都是基于这两幅图的工况）：
刚才前面也说了，LADRC就是等同于一个比例环节Kp+ESO（积分环节）。那为什么PI也是比例环节＋积分环节，为什么PI的超调量那么大？（我就以我做电机控制的角度来看，本人控制理论水平较差。）
这是因为，ESO这个积分环节的输入量是转速估计值与实际值的差值，传统PI调节器的积分环节输入量是转速参考值与实际值的差值。
在没有达到转速参考值之前，传统PI调节器的积分环节输出会不断增大，直到限幅值为止，之后又从限幅值降下来。而对于ESO而言，即使没有达到转速参考值，但是转速估计值与实际值可能都已经完全相等了，所以ESO的积分输出不会再继续增大了，因此就不需要像传统的积分环节进行退饱和。
那我们来对比看看两者的积分项的输出变化：
可以看到，在启动过程中，ESO的积分输出很小，因此也不需要花时间进行退饱和。
可以看到，在启动过程中，PI调节器中的积分输出很大（达到了限幅值25A），因此需要花大量时间进行退饱和。
为什么ESO积分输出和PI调节器中的积分输出在0.2s之后都为10Nm？因为我在0.2s时突加了10Nm。由于两种控制策略都可以实现无差跟踪，所以转速环的Kp输出都为零，所以为了抵抗10Nm的负载，转速环积分输出都为10A。因为我的仿真模型中，1A电流对应1Nm负载，所以10Nm负载就是10A电流。
4.LADRC的鲁棒性
前面已经说到转速环的输入量增益为b0=Ktn/Jn=1.5*Pn*flux/Jn
即转速环的输入量增益与电机极对数Pn、磁链flux、转动惯量Jn有关。
仿真参数如下：
Tpwm = 1e-4;%开关周期
Tspeed = 1e-4;%转速采样周期
Pn = 4;%电机极对数
Ls = 8.5e-3;%定子电感，采用隐极的，Ld=Lq=Ls
Rs = 3;%定子电阻
flux = 0.1688;%永磁体磁链
J = 0.01;%转动惯量
Vdc = 311;%直流母线电压
iqmax = 25;%额定电流
fc = 300;%电流环带宽
Kt = 1.5*Pn*flux;
b = Kt/J;%这个b是完全准确的
%转速环ESO参数
c = 500;
c1 = 2*c;
c2 = c*c;
现在来看看b±变化50%的对比：
可以看的，b为标准值的150%时，转速虽然有点超调，但是这个超调量和调节时间还是明显优于PI调节器的；b为标准值的50%，转速上升的速度稍微有点慢，但是性能还是挺好的，转速也没有超调。
把转速环PI换成LADRC效果还是非常明显的，其实电流环也同理，换成LADRC之后，超调会消失（本文结论）。
从上述几幅图来看（启动过程），只有在转速LADRC，电流环MFPCC-ESO的情况下，转速和q轴电流都没有超调量（q轴电流正比于转矩，q轴电流有没有超调量可以从转矩波形中看出来。
开放原子开发者工作坊旨在鼓励更多人参与开源活动，与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动，如meetup、训练营等，主打技术交流，干货满满，真诚地邀请各位开发者共同参与！
更多推荐
26
0- 0
已为社区贡献24条内容
所有评论(0)