👨‍🎓 个人主页： 研学社的博客

💥💥💞💞 欢迎来到本博客❤️❤️💥💥


🏆 博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。


⛳ 座右铭：行百里者，半于九十。

📋📋📋 本文目录如下：🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现

💥1 概述

灵敏度分析是研究与分析一个系统（或模型）的状态或输出变化对系统参数或周围条件变化的敏感程度的方法。在最优化方法中经常利用灵敏度分析来研究原始数据不准确或发生变化时最优解的稳定性。通过灵敏度分析还可以决定哪些参数对系统或模型有较大的影响。因此，灵敏度分析几乎在所有的运筹学方法以及在对各种方案进行评价时都是很重要的。

灵敏度分析是一种评估模型或系统对其输入参数变化的敏感程度的方法。这种分析有助于理解哪些输入因素对输出结果的影响最大，从而指导决策者聚焦关键变量，提高模型的可靠性和实用性。在进行灵敏度分析的建模时，可以遵循以下步骤：

1. 确定分析目标与模型框架

首先明确你想要通过灵敏度分析解决的问题是什么，以及用于分析的基础模型是什么。这可能是一个数学模型、统计模型、经济模型或是工程仿真模型等。确保模型能够准确反映系统或过程的主要特征。

2. 识别关键输入参数

识别出对模型输出结果有显著影响的输入参数或变量。这些参数可能是直接测量的物理量、假设条件、成本、效率等因素。使用专业知识或先前的研究来初步判断哪些参数最重要。

3. 设定参数变动范围

为每个关键输入参数定义一个合理的变动范围。这个范围应该基于参数的实际情况（如测量误差、历史数据波动范围）和理论极限。变动范围可以是固定百分比变化，也可以是具体的数值区间。

4. 运行模型并收集数据

针对每个关键输入参数的不同取值，运行模型并记录相应的输出结果。这通常需要大量的计算工作，尤其是当模型复杂且参数众多时，可能需要利用计算机程序自动化处理。

5. 分析结果与可视化

分析模型输出如何随着输入参数的变化而变化。常用的分析方法包括：

• Tornado图：展示各参数变化对输出结果的影响大小排序。
• 响应曲面法：构建输入参数与输出结果之间的二维或三维图形，直观显示参数间的关系。
• 敏感性指数：如边际效应、相对灵敏度等指标，量化参数的敏感度。

6. 解释与应用结果

解释灵敏度分析的结果，确定哪些参数是最敏感的，即哪些变量的小幅变动会导致输出结果的大幅变化。这一步骤对于优化模型、减少不确定性、制定策略至关重要。

7. 验证与迭代

验证灵敏度分析结果的合理性，并根据需要调整模型或分析参数，进行迭代分析以不断改进模型的准确性和实用性。

通过上述步骤，可以有效地建立并执行一个灵敏度分析模型，帮助决策者更好地理解系统行为，优化决策过程。

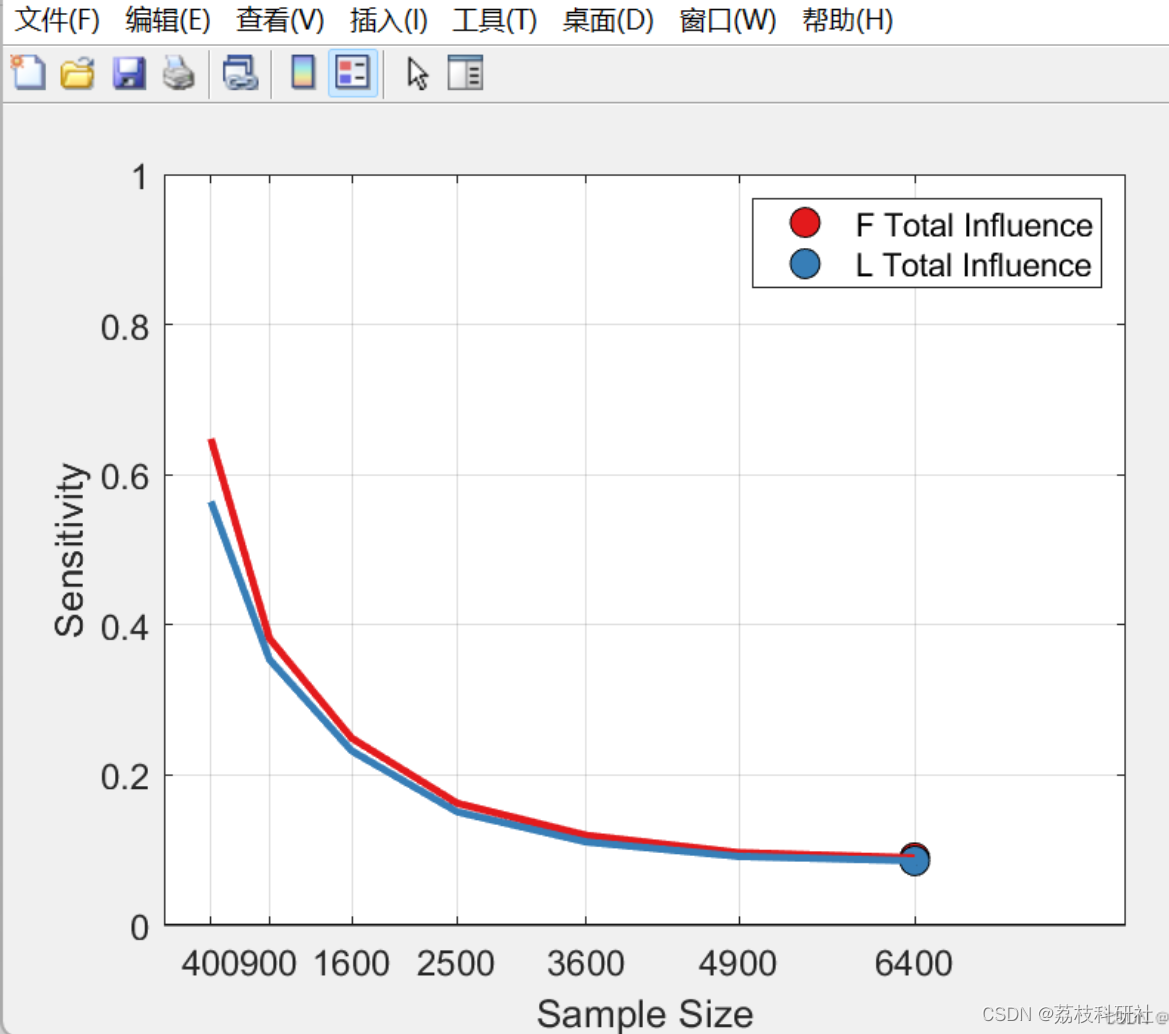
📚2 运行结果

部分代码：

%% STEP 1: Define the Model: Additive Model

close all; clc;

% Constant Definitions

N = 1000; % sample size

R = 50; % R:50 - 200

C = 1 * 10^(-4); %C: 10^-4 - 5*10^-4

tau = R * C;

freq = 50;

period = 1/(2*freq);

w = (2 * pi * freq);

t = 0:0.00001:(period);

% Model Equation Definitions

v1 =@(t) abs(230 * sqrt(2) * cos(w*t));

t1 = (1/w) * atan(1/(w*tau));

A = 230 * sqrt(2) * cos(w*t1) * exp(t1/tau);

v2 =@(t) A * exp(-t/tau);

% Calculate Maximum Voltage

vMax = 230*sqrt(2);

% Calculate Minimum Voltage

myfunc = @(t2) A*exp(-t2/tau) + sqrt(2)*230*cos(w*t2);

opts = optimset('Diagnostics','off', 'Display','off');

t2 = fsolve(myfunc, period/2, opts);

vMin = v2(t2);

% Calculate deltaV

deltaV = vMax - vMin;

🎉3 参考文献

部分理论来源于网络，如有侵权请联系删除。

[1]Zhao Zhao, Lu Zhao Hui,and Zhao Yan Gang."An efficient method for predictive-failure-probability-based global sensitivity analysis." Structural and Multidisciplinary Optimization 65.11(2022). doi:10.1007/S00158-022-03434-3.

🌈4 Matlab代码实现