【排序算法】快速排序、冒泡排序

情况时间复杂度空间复杂度最好情况O(n log n)O(log n)最坏情况O(n^2)O(n)平均情况O(n log n)O(log n)时间复杂度：快速排序的平均和最好情况时间复杂度为O(n log n)，但在最坏情况下可能会退化为O(n^2)。空间复杂度：快速排序是原地排序算法，额外的空间复杂度为O(1)，但递归栈的空间消耗取决于递归深度，平均为O(log n)，最坏情况下为O(n)。通过合

勇敢勇勇不怕困难_

2160人浏览 · 2024-10-11 12:09:02

勇敢勇勇不怕困难_ · 2024-10-11 12:09:02 发布

文章目录

快速排序
冒泡排序
- 时间复杂度

快速排序

1.hoare版本（左右指针法）

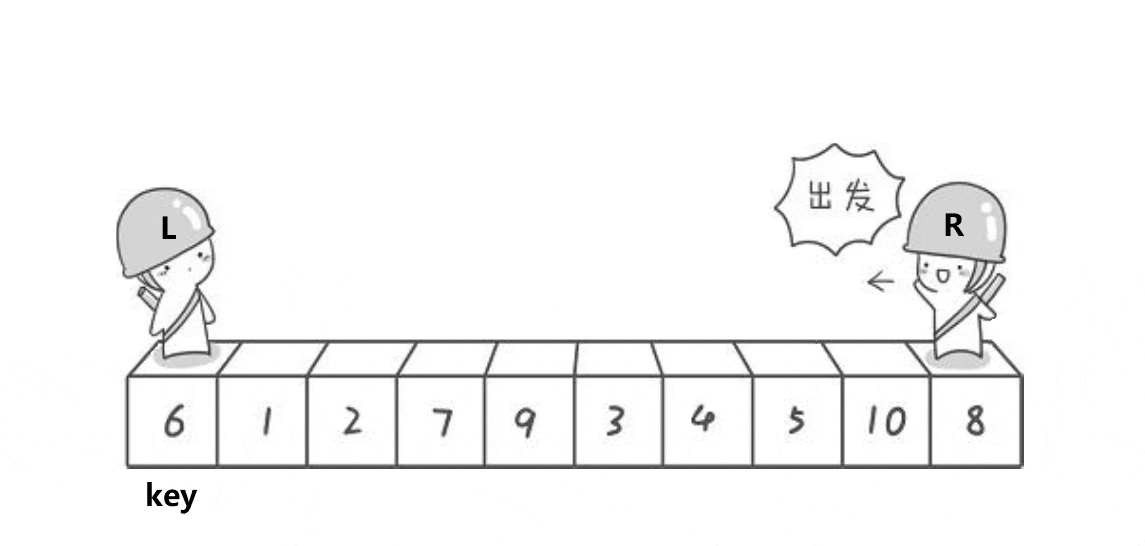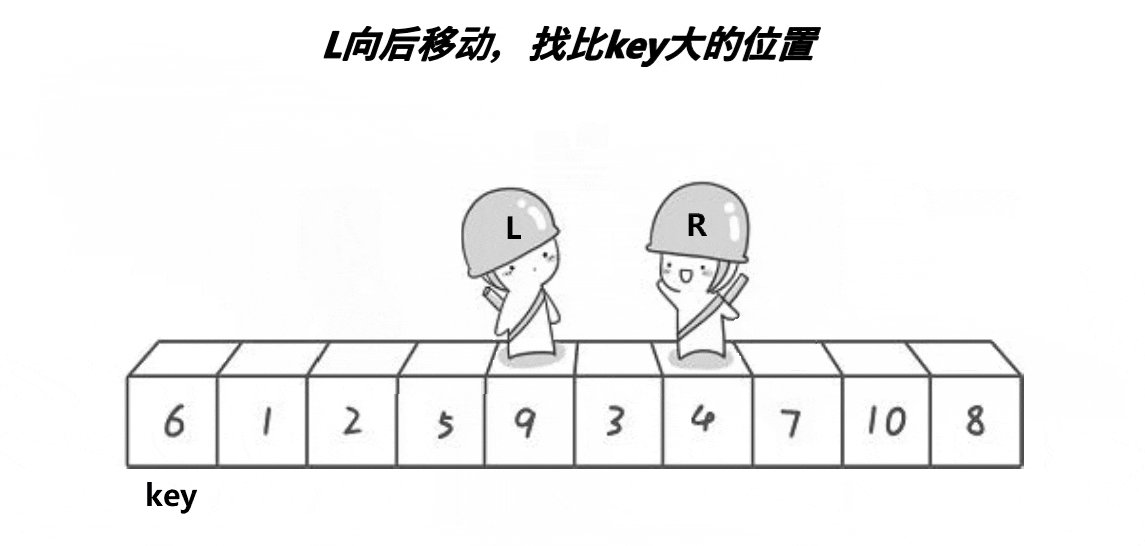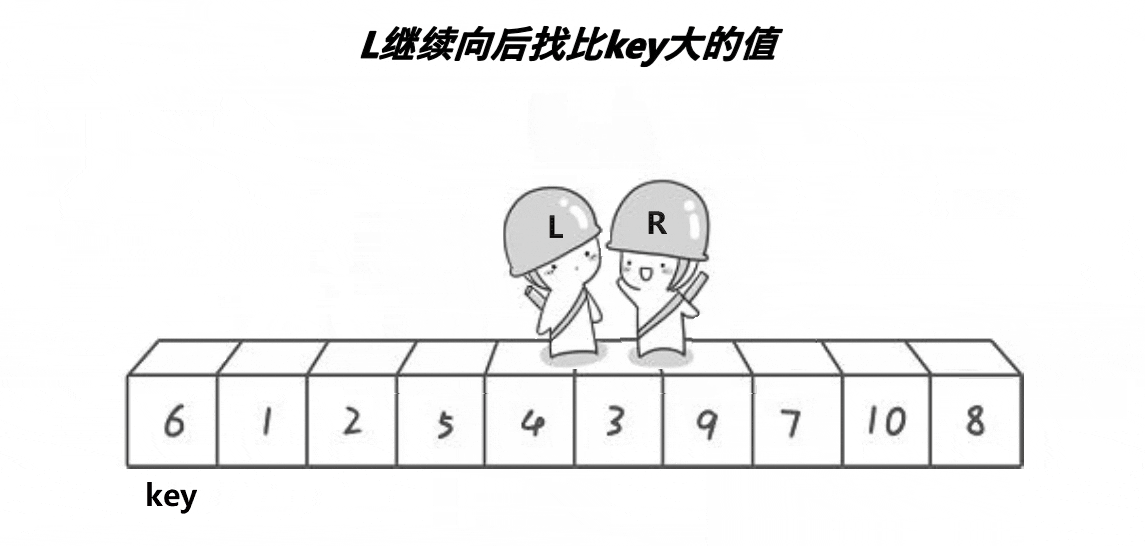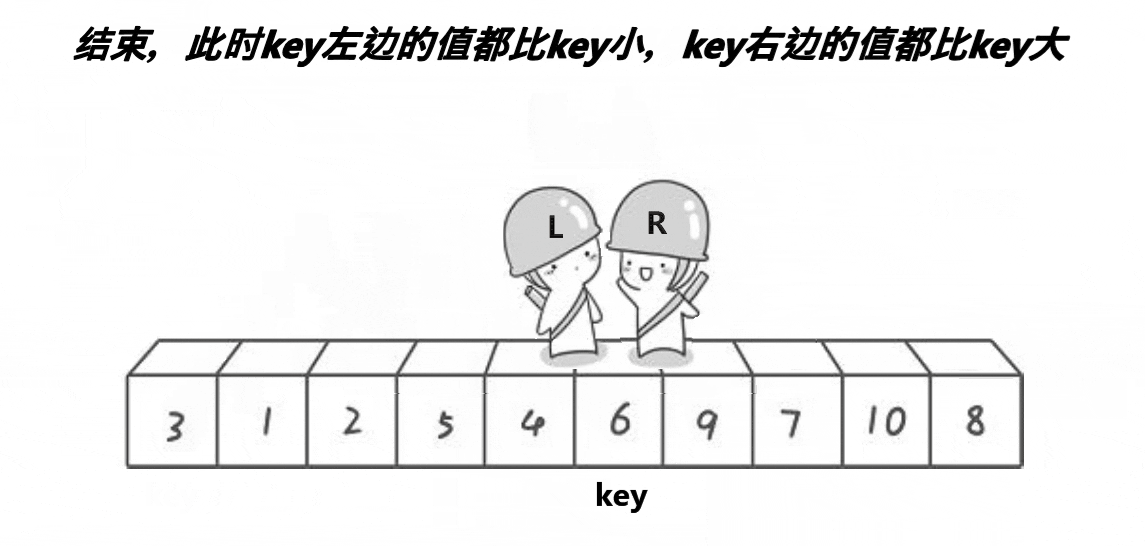
代码：

int PartSort1(int* a, int left, int right)
{
    // 使用三数取中法获取基准值的下标
    int midi = GetMidi(a, left, right);
    Swap(&a[left], &a[midi]); // 将基准值移到最左边

    int keyi = left; // 基准值的下标
    while (left < right) // 当左指针小于右指针时循环
    {
        // 从右侧开始，找到小于基准值的元素
        while (left < right && a[right] >= a[keyi])
        {
            --right;
        }
        // 从左侧开始，找到大于基准值的元素
        while (left < right && a[left] <= a[keyi])
        {
            ++left;
        }
        // 交换找到的两个元素
        Swap(&a[left], &a[right]);
    }
    // 将基准值放到正确的位置
    Swap(&a[keyi], &a[left]);
    return left; // 返回基准值的位置
}

时间复杂度、空间复杂度分析

快速排序（QuickSort）是非常经典的排序算法之一，它通过分治法来解决排序问题。快速排序的效率取决于如何选择基准值（pivot）以及每次分区的结果。

1. 时间复杂度分析

最好情况时间复杂度：`O(n log n)`

情况：每次选择的基准值都能将数组均匀地分为两部分。

分析：
- 在理想情况下，每次分区基准值都能将数组分为大约等长的两部分，左半部分和右半部分各包含 n/2 个元素。
- 每次递归调用之后，问题规模减少一半。递归深度为 log n，因为每次递归调用都会将问题规模缩小一半。
- 在每一层递归中，我们需要做 O(n) 的比较和交换操作（因为需要遍历整个数组来进行分区操作）。
- 因此，最好情况下的总时间复杂度为 O(n) * O(log n) = O(n log n)。

最坏情况时间复杂度：`O(n^2)`

**情况**：每次选择的基准值都是数组中的最大值或最小值，导致每次分区都只将数组分成一小部分。

分析：
- 在最坏情况下，选择的基准值总是最大或最小值。例如，当数组本身是有序的（升序或降序），而基准值选择的是首元素或尾元素。
- 每次递归只能减少一个元素，导致需要递归 n 次，每次分区的时间复杂度为 O(n)。
- 总的递归深度为 n，所以最坏情况下的时间复杂度为 O(n) * O(n) = O(n^2)。

平均情况时间复杂度：`O(n log n)`

情况：基准值的选择是随机的，不偏向最优或最坏的情况。

分析：
- 在大多数情况下，基准值不会总是选择极端的最大值或最小值，也不会总是完美地将数组一分为二。
- 虽然递归深度介于 log n 和 n 之间，但在平均情况下，递归深度为 O(log n)，每次分区操作依旧是 O(n)。
- 因此，平均情况下的时间复杂度仍为 O(n log n)。

2. 空间复杂度分析

递归导致的空间消耗

递归调用栈：快速排序是递归算法，空间复杂度主要取决于递归调用栈的深度。
- 最好情况：递归树的深度为 log n，对应的空间复杂度为 O(log n)。
- 最坏情况：递归树的深度为 n，对应的空间复杂度为 O(n)。这是当每次分区只减少一个元素的极端情况，比如数组已经有序的情况下。

原地排序特性

额外空间开销：快速排序是一种原地排序算法，在排序过程中不需要额外的数组，所有的交换操作都在原数组上进行。
除了递归调用栈外，快速排序的额外空间复杂度为 O(1)。

3. 各种情况下的复杂度总结

情况	时间复杂度	空间复杂度
最好情况	`O(n log n)`	`O(log n)`
最坏情况	`O(n^2)`	`O(n)`
平均情况	`O(n log n)`	`O(log n)`

4. 优化策略

1. 三数取中法

为了避免最坏情况（如数组已经有序），可以使用三数取中法选取基准值。这样能够有效避免最坏的分区情况，使得基准值更接近数组的中间值，从而提升排序的效率，避免时间复杂度退化为 O(n^2)。

2. 随机化选择基准值

通过随机选择基准值，可以避免输入数据对算法性能的影响，使得平均时间复杂度趋于 O(n log n)，降低出现最坏情况的概率。

3. 小区间优化

当子序列的长度较小时（如 n <= 10），可以使用插入排序代替快速排序进行排序。插入排序在小数组上表现得更好，从而提升整体的排序性能。

总结

时间复杂度：快速排序的平均和最好情况时间复杂度为 O(n log n)，但在最坏情况下可能会退化为 O(n^2)。
空间复杂度：快速排序是原地排序算法，额外的空间复杂度为 O(1)，但递归栈的空间消耗取决于递归深度，平均为 O(log n)，最坏情况下为 O(n)。

通过合理的基准值选择（如三数取中法）和优化手段，快速排序在实践中通常表现出非常高效的 O(n log n) 的性能。

优化——三数取中法

三数取中法是快速排序中的一种优化策略，用来选择基准值（pivot），避免退化成不理想的时间复杂度，特别是在数组有序或接近有序时。

1. 三数取中法的原理

快速排序的效率依赖于基准值的选取。如果每次选择的基准值太大或太小，就会导致分区不均匀，进而降低排序效率。三数取中法通过选取数组中的 三个关键位置 的元素，并取这三个元素的中位数作为基准值，以此来避免极端情况的发生。

通常从 数组最左端、数组最右端 和 数组中间 选取三个元素。
然后将这三个元素的中位数（即三者的中间值）作为基准值。

这种方法能够增加选取基准值的随机性，使得分区更加均衡，从而提高了排序的效率，避免了快速排序退化成 O(n²) 的情况。

2. 三数取中法的步骤
假设我们有一个数组 arr，它的长度是 n。我们选择数组的三个关键元素：

最左边的元素：arr[left]
最右边的元素：arr[right]
中间的元素：arr[mid]，其中 mid = left + (right - left) / 2

步骤如下：

从 arr[left]，arr[mid] 和 arr[right] 中选出中间大小的那个值作为基准值 pivot。
将这个基准值放到 arr[left] 的位置（如果选取的基准值不是 arr[left]，就将其与 arr[left] 进行交换）。
使用快速排序的常规分区过程，进行递归排序。

3.三数取中法的代码实现
接下来是使用三数取中法优化的快速排序代码（C语言实现）：

// 三数取中法，返回基准值的位置
int GetMidi(int* a, int left, int right)
{
    int mid = (left + right) / 2; // 计算中间位置
    // 比较 left、mid 和 right 三个值，选择中位数作为基准
    if (a[left] < a[mid])
    {
        if (a[right] > a[mid]) // mid 是中间值
        {
            return mid;
        }
        else if (a[left] > a[right]) // left 是最大值
        {
            return left;
        }
        else // right 是最大值
        {
            return right;
        }
    }
    else // a[left] > a[mid]
    {
        if (a[mid] > a[right]) // mid 是中间值
        {
            return mid;
        }
        else if (a[right] > a[left]) // left 是最大值
        {
            return left;
        }
        else // right 是最大值
        {
            return right;
        }
    }
}

// 分区函数
int PartSort1(int* a, int left, int right)
{
    // 使用三数取中法获取基准值的下标
    int midi = GetMidi(a, left, right);
    Swap(&a[left], &a[midi]); // 将基准值移到最左边

    int keyi = left; // 基准值的下标
    while (left < right) // 当左指针小于右指针时循环
    {
        // 从右侧开始，找到小于基准值的元素
        while (left < right && a[right] >= a[keyi])
        {
            --right;
        }
        // 从左侧开始，找到大于基准值的元素
        while (left < right && a[left] <= a[keyi])
        {
            ++left;
        }
        // 交换找到的两个元素
        Swap(&a[left], &a[right]);
    }
    // 将基准值放到正确的位置
    Swap(&a[keyi], &a[left]);
    return left; // 返回基准值的位置
}

// 快速排序主函数
void QuickSort2(int* a, int begin, int end)
{
    // 递归终止条件：当子序列长度小于等于1时，返回
    if (begin >= end)
        return;

    // 使用分区函数将数组划分为两部分
    int keyi = PartSort1(a, begin, end);
    // 递归处理左子序列 [begin, keyi-1]
    QuickSort2(a, begin, keyi - 1);
    // 递归处理右子序列 [keyi+1, end]
    QuickSort2(a, keyi + 1, end);
}

4. 三数取中法的运作过程（例子讲解）
假设我们有一个数组：[29, 10, 14, 37, 13, 50, 31, 28]，并使用快速排序对其进行排序。

第一次选取基准值：
- 左边的元素：arr[0] = 29
- 右边的元素：arr[7] = 28
- 中间的元素：arr[3] = 37
- 经过排序后：arr[0] = 29, arr[3] = 37, arr[7] = 28
- 三数中位数是 29，选择 29 作为基准值，并将其放到 arr[0] 位置。
第一次分区：
- 开始快速排序的分区操作：将小于 29 的元素移到左边，大于 29 的元素移到右边。
- 得到分区结果，假设分区后得到的数组是：[10, 14, 13, 28, 29, 50, 31, 37]。
递归操作：
- 继续对左边子数组 [10, 14, 13, 28] 和右边子数组 [50, 31, 37] 进行快速排序。
- 每次使用三数取中法选择基准值，并进行递归分区。

5. 为什么三数取中法能够避免退化？

在有序或接近有序的数组中，简单地选择最左或最右的元素作为基准值可能导致分区非常不均匀，导致快速排序退化为 O(n²)。而三数取中法通过从三个位置选取基准值，有效减少了选到极值的概率，从而使分区更加均匀，降低了退化为 O(n²)的可能性。

总的来说，三数取中法能够提高快速排序的稳定性和效率，是一种非常常见且有效的优化策略。

2.挖坑法

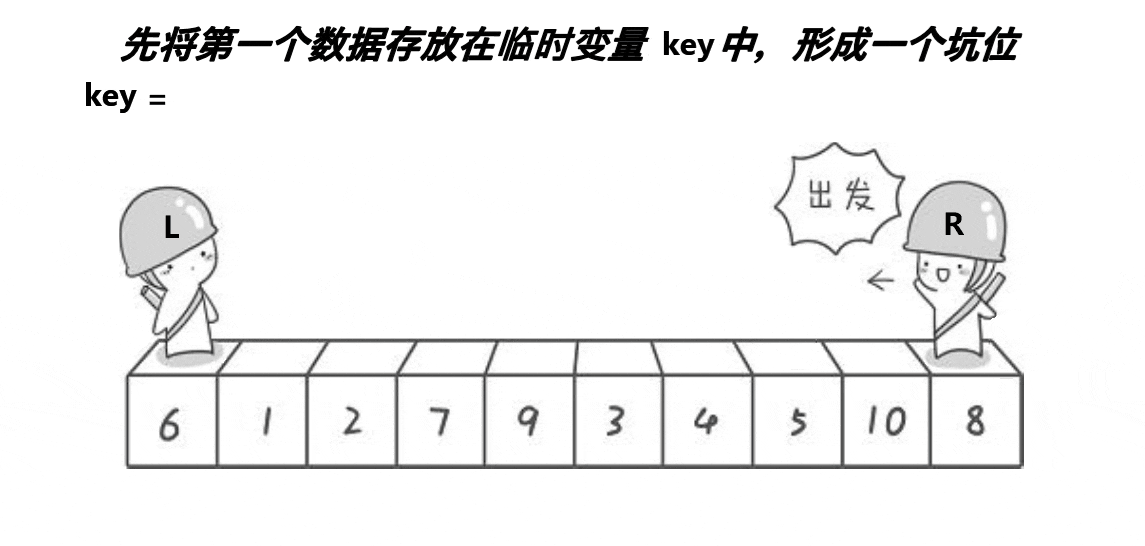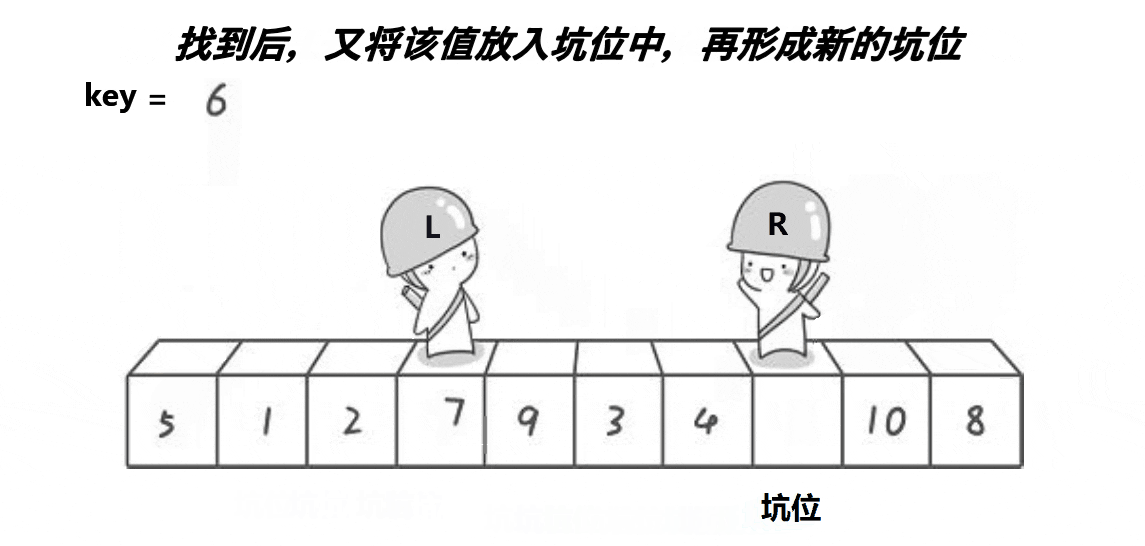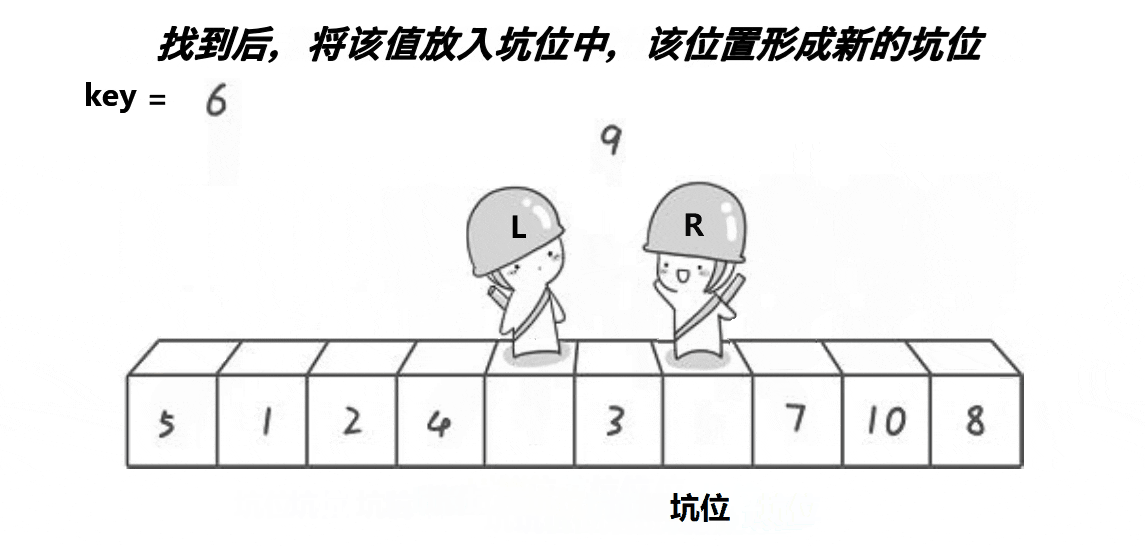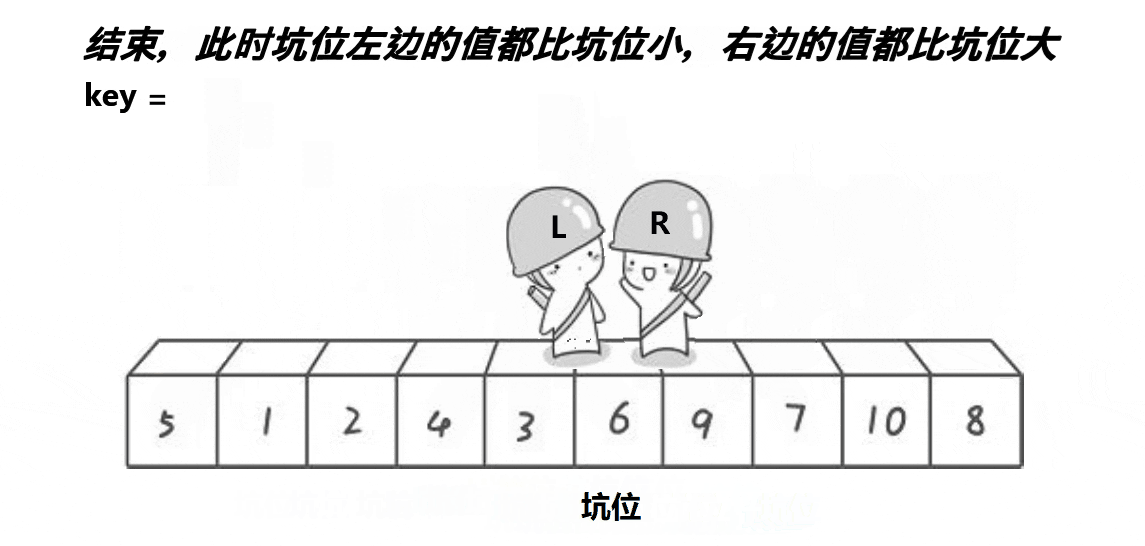
快速排序中的 挖坑法 是另一种实现快速排序的方法。相比于“左右指针法”，挖坑法使用的是先将基准值“挖出来”放在一个临时位置，随后通过逐步填坑的方式进行排序。这种方法简洁清晰，易于理解。

挖坑法的思路

挖坑法的核心思路是：

首先选择一个基准值（一般是最左边或最右边的元素），将其从数组中暂时“挖出来”。
从剩下的元素中，依次从另一端向中间遍历，寻找需要“填坑”的元素。
每次找到一个符合条件的元素后，填入当前的坑位置，然后在被填元素的位置留下一个新的坑。
直到左右指针相遇，将基准值填入最后留下的坑。

挖坑法的步骤

假设我们选择数组最左边的元素作为基准值 pivot，挖坑法的详细步骤如下：

挖坑：选择数组的第一个元素作为基准值，记为 pivot，并将其位置视为第一个“坑”。
从右向左扫描：从右边开始，找到第一个小于 pivot 的元素，将其填入左边的坑。
从左向右扫描：从左边开始，找到第一个大于 pivot 的元素，将其填入右边的坑。
重复步骤 2 和 3，直到左右指针相遇为止。
将 pivot 填回：当左右指针相遇时，将基准值 pivot 填入最后一个坑的位置，此时基准值已经位于正确的位置。
挖坑法的代码实现

下面是快速排序中挖坑法的 C 语言代码：

int PartSort2(int* a, int left, int right) {
    // 使用三数取中法获取基准值的下标
    int midi = GetMidi(a, left, right);
    // 将基准值（中间值）交换到数组的最左边
    Swap(&a[left], &a[midi]);
    
    // 保存基准值
    int keyi = a[left];
    // 初始化“坑”的位置，指向基准值的位置
    int hole = left;

    // 分区过程
    while (left < right) {
        // 从右侧开始，找到第一个小于基准值的元素
        while (left < right && a[right] >= keyi) {
            right--;
        }
        // 将找到的元素放入“坑”中
        a[hole] = a[right];
        // 更新“坑”的位置
        hole = right;

        // 从左侧开始，找到第一个大于基准值的元素
        while (left < right && a[left] <= keyi) {
            left++;
        }
        // 将找到的元素放入“坑”中
        a[hole] = a[left];
        // 更新“坑”的位置
        hole = left;
    }

    // 将基准值放入最终位置
    a[hole] = keyi;
    // 返回基准值的位置
    return left;
}

挖坑法的过程解析（详细示例）

我们以数组 arr[] = {6, 1, 2, 7, 9, 3, 4, 5, 10, 8} 为例，详细讲解挖坑法的快速排序过程：

挖坑：

选择 arr[0] = 6 作为基准值 pivot，并把这个位置当作第一个“坑”。
此时 l = 0, r = 9，数组为 [6, 1, 2, 7, 9, 3, 4, 5, 10, 8]。

从右向左扫描：

从右向左扫描，r 逐渐减少。
arr[9] = 8 大于 pivot，继续扫描。
arr[8] = 10 大于 pivot，继续扫描。
arr[7] = 5 小于 pivot，将 arr[7] 填入 arr[0] 的坑，l 位置就成为了新的坑。此时数组为：[5, 1, 2, 7, 9, 3, 4, 5, 10, 8]，并且 r = 7。

从左向右扫描：

从左向右扫描，l 逐渐增加。
arr[1] = 1 小于 pivot，继续扫描。
arr[2] = 2 小于 pivot，继续扫描。
arr[3] = 7 大于 pivot，将 arr[3] 填入 arr[7] 的坑。此时数组为：[5, 1, 2, 7, 9, 3, 4, 7, 10, 8]，并且 l = 3。

从右向左继续扫描：

从右向左扫描，r = 6 开始。
arr[6] = 4 小于 pivot，将 arr[6] 填入 arr[3] 的坑，l = 6 成为新的坑。此时数组为：[5, 1, 2, 4, 9, 3, 4, 7, 10, 8]，并且 r = 6。

将基准值放回坑中：

此时左右指针相遇，l = r = 3。
将基准值 pivot = 6 放回 arr[3]。数组最终变成：[5, 1, 2, 6, 9, 3, 4, 7, 10, 8]。

递归操作：

继续对基准值左边 [5, 1, 2] 和右边 [9, 3, 4, 7, 10, 8] 进行递归排序。

挖坑法的优点

挖坑法的核心逻辑清晰，理解起来简单，通过逐步填坑的方式可以避免多次交换。
在元素个数较少的情况下，挖坑法的实际效率较高。

与左右指针法的对比

相同点：两种方法的核心思路都是通过分区使得基准值的左侧全是小于基准值的元素，右侧全是大于基准值的元素。
不同点：左右指针法直接交换元素，而挖坑法通过“挖坑”和“填坑”的方式逐步调整数组。

3.前后指针版本

前后指针法是一种常见的快速排序分区算法，用于将数组划分为两部分：一部分小于基准值，另一部分大于基准值。不同于 左右指针法（如 Hoare 分区法），前后指针法使用两个指针：一个指针（pre）表示已经处理过的部分，另一个指针（cur）表示当前正在处理的元素。前后指针法的主要思想是通过移动 cur，将小于基准值的元素不断放到前面部分，而 pre 指向小于基准值的最后一个位置。

详细解释

初始化：
- key = left：选择 a[left] 作为基准值。
- prev = left：初始化 prev 指向基准值的位置，表示小于基准值的最后一个元素的索引。
- cur = prev + 1：cur 从 prev 的下一个元素开始，用于遍历数组。
遍历数组：
- while (cur <= right)：遍历从 cur 到 right 的元素。
- 在每次循环中，检查 a[cur] 是否小于基准值 a[key]。
更新小于基准的部分：
- 如果 a[cur] < a[key]，则说明当前元素应当被移动到小于基准值的部分。
- prev++：更新 prev 的位置，表示小于基准值的部分增加了一个元素。
- if (prev != cur)：在交换前，检查 prev 和 cur 是否相同。如果相同，说明当前元素已经在正确位置，不需要交换。
交换：
- Swap(&a[prev], &a[cur])：如果 prev 和 cur 不同，交换这两个元素。这一步确保所有小于基准值的元素都被移到数组的前面。
移动指针：
- cur++：继续遍历下一个元素。
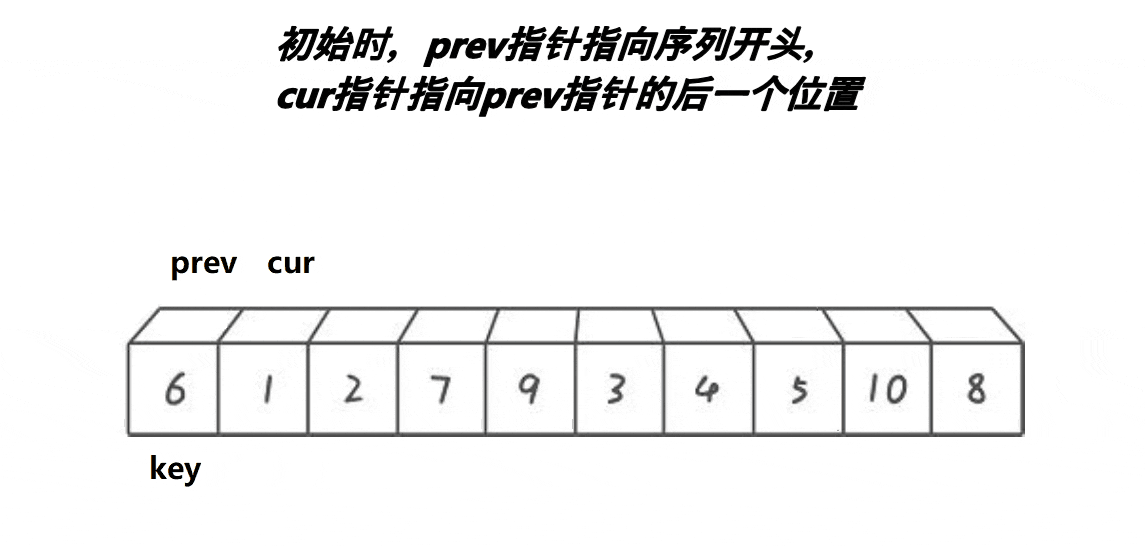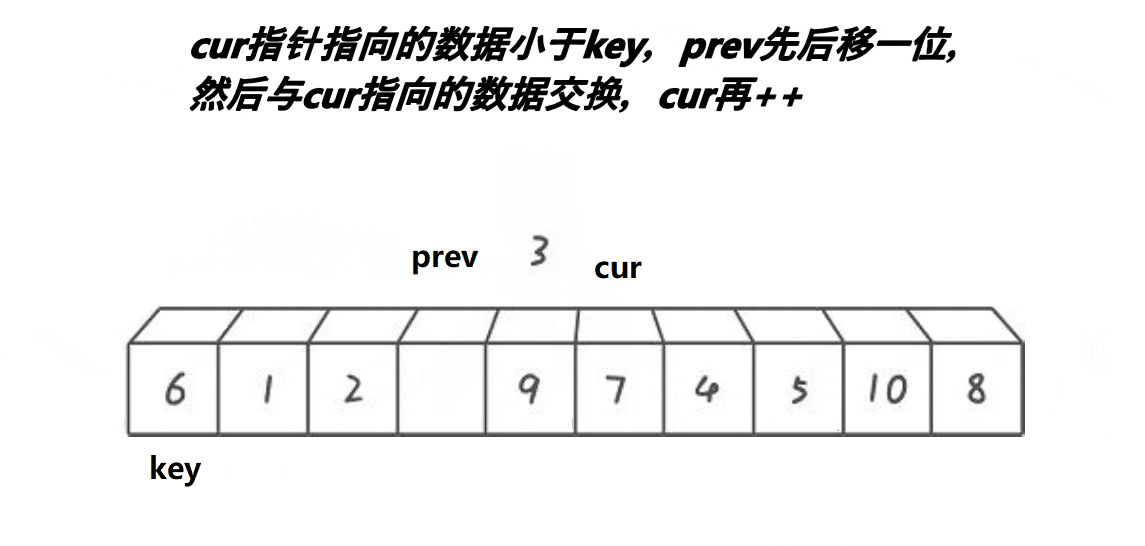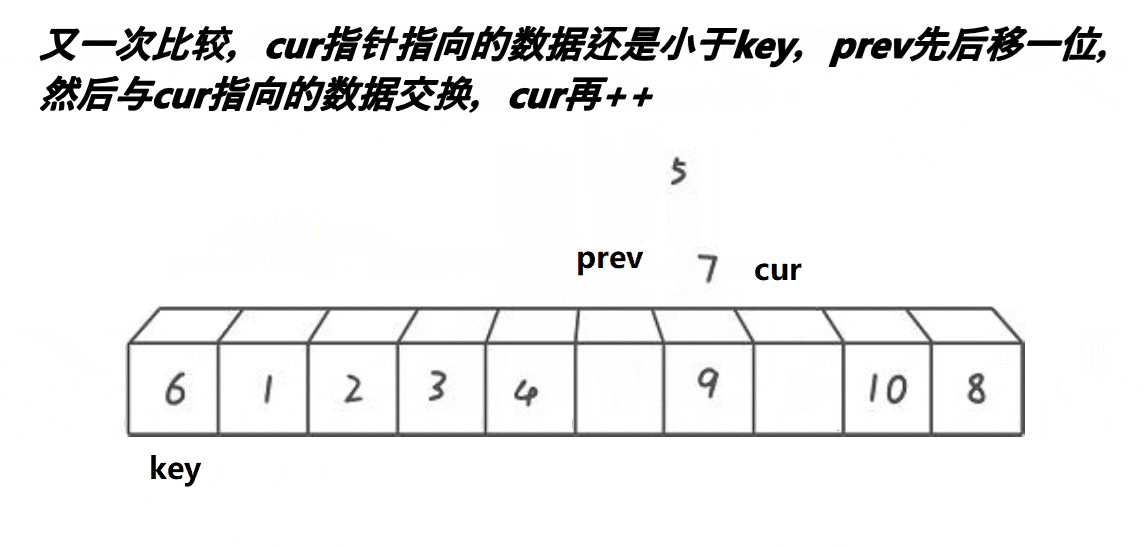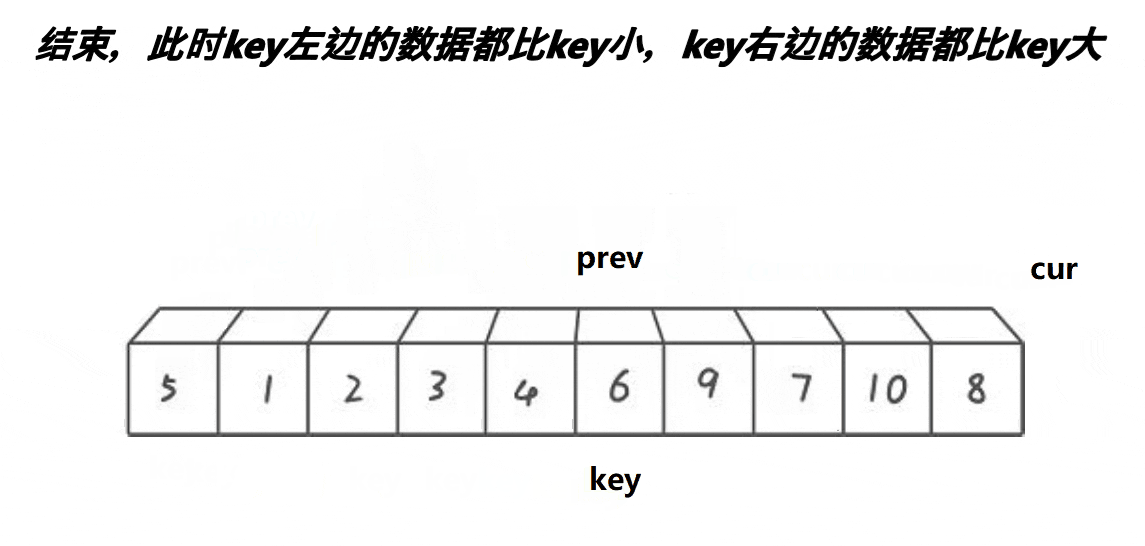
将基准值放到正确位置：
- 循环结束后，所有小于基准值的元素已经被放置在 a[left] 的左侧。
- Swap(&a[prev], &a[key])：将基准值放到它应该在的位置（prev），即所有小于基准值的元素的右侧。
返回基准值的位置：
- return prev：返回基准值的新位置，供后续递归使用。

代码实现（C语言）

int PartSort3(int* a, int left, int right)
{
    int key = left;       // 基准元素的索引
    int prev = left;      // 小于基准的最后一个元素的索引
    int cur = prev + 1;   // 当前指针，从下一个元素开始

    while (cur <= right)
    {
        if (a[cur] < a[key]) // 如果当前元素小于基准值
        {
            // 先更新prev
            prev++; 
            // 只有当prev与cur不同的时候才进行交换
            if (prev != cur) 
            {
                Swap(&a[prev], &a[cur]);
            }
        }
        cur++; // 移动当前指针
    }
    // 将基准值放到正确的位置
    Swap(&a[prev], &a[key]); 
    return prev; // 返回基准值的新位置
}


// 快速排序函数
void QuickSort2(int* a, int begin, int end)
{
	//递归终止条件：当子序列长度小于等于1时，返回
	if (begin >= end)
		return;
	//使用分区函数(前后指针法)将数组划分为两部分
	int keyi = PartSort3(a, begin, end);
	// [begin, keyi-1] keyi [keyi+1, end]
	QuickSort2(a, begin, keyi - 1);// 递归处理左子序列 [begin, keyi-1]
	QuickSort2(a, keyi + 1, end);//   递归处理右子序列 [keyi+1, end]
}

示例：排序 6 1 2 7 9 3 4 5 10 8

假设数组是 {6, 1, 2, 7, 9, 3, 4, 5, 10, 8}，通过前后指针法进行快速排序：

第一次调用 Partition()`：
- pivot = 8，pre = -1，cur 从 0 到 8 依次遍历。
- 遍历时，6, 1, 2, 7, 3, 4, 5 都比 8 小，依次与 pre 后面的元素交换。最后，pre 的值为 6，表示小于 8 的部分。
- 最后交换 pivot（8）和 pre + 1（9 位置的元素），数组变成 {6, 1, 2, 7, 3, 4, 5, 8, 10, 9}。
接下来的递归：
- 左侧部分 {6, 1, 2, 7, 3, 4, 5} 继续排序，右侧部分 {10, 9} 继续排序。
经过递归后，最终数组排序完成。

前后指针法的优势

前后指针法相比其他分区方法，尤其是在处理大量重复元素时表现较好。因为它只在必要时交换元素，避免了不必要的交换操作。

关键点：

pre 的作用：pre 始终指向小于基准值的最后一个元素，通过 cur 的遍历，保证小于基准值的元素不断被交换到 pre 之前的区域。
为什么基准值最终放在 pre + 1：当 cur 完全扫描完数组后，pre + 1 就是第一个大于基准值的位置，因此基准值放在 pre + 1，即可保证基准值左边全小于等于它，右边全大于等于它。

总结

前后指针法是一种简洁高效的分区策略，特别适合处理大量重复元素或结构不规则的数组。

分治法是快速排序的核心思想。它通过递归地将问题分解为较小的子问题，逐步解决

第二种和第三种与第一种只是单纯的思想不一样而已，性能没有区别。

优化：小区间优化

//区间优化
void QuickSort1(int* a, int begin, int end)
{
	if (begin >= end)
		return;
	if (end - begin + 1 > 10)
	{
		int keyi = PartSort3(a, begin, end);
		QuickSort1(a, begin, keyi - 1);
		QuickSort1(a, keyi + 1, end);
	}
	else
	{
		InsertSort(a + begin, end - begin + 1);
		//a + begin 是为了将数组的起始位置偏移到 begin 处，从而对局部子数组 [begin, end] 进行插入排序。
	}
}

void QuickSort2(int* a, int begin, int end)
{
	//递归终止条件：当子序列长度小于等于1时，返回
	if (begin >= end)
		return;
	//使用分区函数(前后指针法)将数组划分为两部分
	int keyi = PartSort3(a, begin, end);
	// [begin, keyi-1] keyi [keyi+1, end]
	QuickSort2(a, begin, keyi - 1);// 递归处理左子序列 [begin, keyi-1]
	QuickSort2(a, keyi + 1, end);//   递归处理右子序列 [keyi+1, end]
}

在这段代码中，QuickSort1 和 QuickSort2 的主要区别是 小区间优化，这是针对递归次数和排序效率进行的一种改进。

小区间优化：

原理：
快速排序在递归的过程中，如果子数组的长度很短，比如 10 个元素以内，递归分割的优势会逐渐减弱。此时，递归的开销反而变得较大，且对小区间执行快速排序不如简单排序（如插入排序）有效。因为插入排序在处理小数据集时的效率比快速排序更高。
QuickSort1的优化机制：
- 当子数组的长度（end - begin + 1）小于等于 10 时，不再继续递归分割，而是直接调用插入排序 (InsertSort) 来对小区间进行排序。
- 插入排序的效率在小数据集上表现非常好，避免了不必要的递归，减少了递归深度，从而降低了递归的开销。

具体作用：

递归深度减少：每一次递归都需要保存栈帧，过多的递归会带来额外的内存开销。通过对小区间使用插入排序，可以有效减少递归的层次。
提高效率：插入排序对小数组的表现优于快速排序。快速排序在小区间上反复递归分割可能带来不必要的开销，而插入排序能够更直接地完成任务。

代码解释：

if ((end - begin + 1) > 10) {
    int keyi = PartSort3(a, begin, end);
    QuickSort1(a, begin, keyi - 1);
    QuickSort1(a, keyi + 1, end);
} 
else {
    InsertSort(a + begin, end - begin + 1);
}

当子数组大小大于 10 时，继续使用快速排序分割并递归；当子数组大小小于或等于 10 时，直接使用插入排序。

QuickSort2 和 QuickSort1 的区别：

QuickSort2 并没有进行小区间优化，始终使用递归的方式分割数组。
QuickSort1 则针对长度较短的子数组使用插入排序，从而提高效率。

小区间优化的意义：

减少递归次数：避免不必要的递归，减少系统栈的使用，降低递归深度。
提高排序效率：在处理小区间时，插入排序比快速排序的效率更高，能够减少排序的时间开销。

因此，在实际应用中，小区间优化能够使得快速排序在平均情况下表现更好，尤其是当数据集较大时，这种优化能明显提升性能。

快速排序非递归代码——借助栈

快速排序的非递归实现主要依赖于 显式栈，用于模拟递归的过程。通常在递归版的快速排序中，递归函数会将未处理的子区间（即左右子数组）作为参数进行递归调用，而在非递归版本中，显式栈用于保存这些子区间的起始和结束索引。

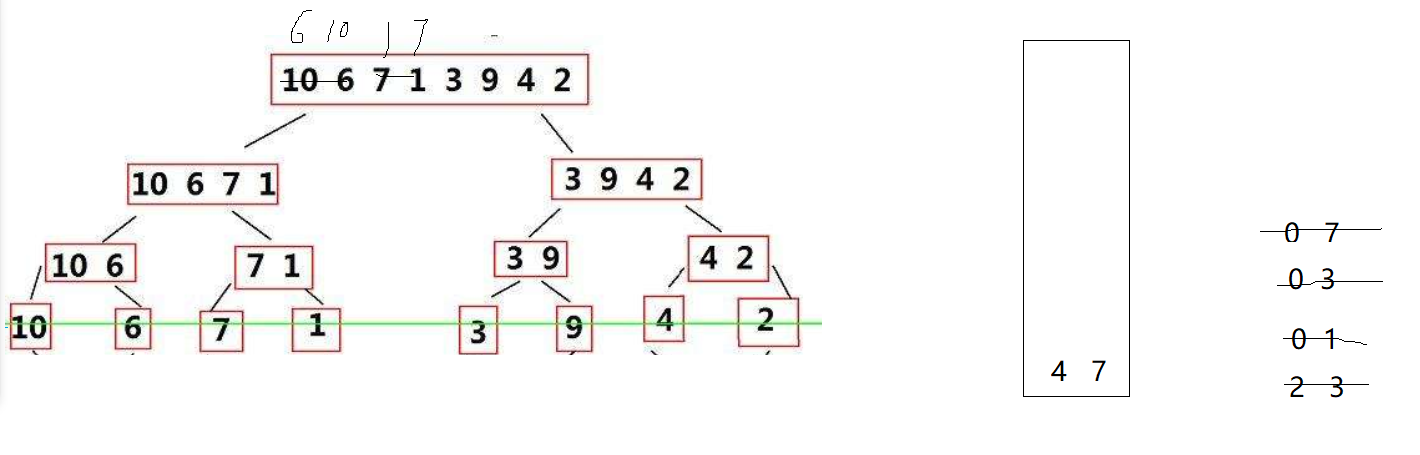
快速排序非递归实现的核心思路：

栈模拟递归：用栈来存储待处理的子区间的边界（即左右子数组的 begin 和 end）。在栈中存储每个子区间的起始和结束位置，然后依次处理栈中的区间，类似于递归时回溯未处理的子区间。
每次分区后入栈左右区间：使用 PartSort（如前后指针法、挖坑法、Hoare法等）对当前区间进行分区，找到基准值的位置 pivot。然后将基准值的左侧区间和右侧区间分别压入栈中等待处理。
栈的使用：使用一个显式栈，每次从栈顶弹出一个子区间进行分割。分割后，将子区间的左右子数组继续压入栈中，直到栈为空为止。

代码：

void QuickSortNonR(int* a, int begin, int end)
{
    ST st;                  // 创建一个栈，用来模拟递归调用栈
    STInit(&st);            // 初始化栈
    STPush(&st, end);       // 将初始的右边界（end）压入栈中
    STPush(&st, begin);     // 将初始的左边界（begin）压入栈中
    
    // 栈为空时表示排序完成
    while (!STEmpty(&st))
    {
        // 从栈中弹出当前处理的区间左右边界
        int left = STTop(&st);   // 获取栈顶元素，赋值给left（当前区间的左边界）
        STPop(&st);              // 弹出栈顶元素

        int right = STTop(&st);  // 获取栈顶元素，赋值给right（当前区间的右边界）
        STPop(&st);              // 弹出栈顶元素

        // 对当前区间进行分割操作，返回基准元素的位置（keyi）
        int keyi = PartSort1(a, left, right);
//keyi 处的值已经经过了排序，具体来说是经过了分区操作
//它的位置已经确定，不需要再对它进行排序
 



//在栈中，我们不会再对 keyi 位置上的值进行处理，因为它已经处于正确的位置。
        // 处理右半部分：[keyi + 1, right]
        if (keyi + 1 < right)    // 如果右半部分长度大于1
        {
            STPush(&st, right);  // 将右半部分的右边界压入栈中
            STPush(&st, keyi + 1); // 将右半部分的左边界（keyi+1）压入栈中
        }

        // 处理左半部分：[left, keyi - 1]
        if (left < keyi - 1)     // 如果左半部分长度大于1
        {
            STPush(&st, keyi - 1); // 将左半部分的右边界（keyi-1）压入栈中
            STPush(&st, left);     // 将左半部分的左边界压入栈中
        }
    }

    STDestroy(&st);  // 栈的所有操作完成后，销毁栈，释放内存
}

这个非递归快速排序算法的实现是通过使用显式栈来替代递归调用，从而避免递归带来的栈深度限制问题。为了理解这个代码，我们需要详细解释每个步骤的思路和实现。

快速排序基本思想回顾：

快速排序通过递归或非递归的方式对数组进行排序。它的核心思想是分区，即通过选择一个基准值（pivot）将数组分成两部分：左侧小于等于基准值，右侧大于基准值。然后分别对这两个部分进行排序。

代码思路详解：

栈的初始化：

ST st;
STInit(&st);
STPush(&st, end);
STPush(&st, begin);

这里首先创建了一个栈 st，用于模拟递归过程。栈的作用是保存当前需要处理的区间的左右边界 begin 和 end。通过 STPush 将初始区间 [begin, end] 压入栈中。

STPush(&st, end)：将数组的右边界压入栈。
STPush(&st, begin)：将数组的左边界压入栈。

栈中每一对元素表示一个待处理的区间，栈顶元素表示当前需要处理的区间的边界。

主循环（非递归的核心部分）：

while (!STEmpty(&st))
{
    int left = STTop(&st);
    STPop(&st);

    int right = STTop(&st);
    STPop(&st);

通过 STEmpty(&st) 判断栈是否为空，如果栈非空，则说明还有未处理的区间。

通过 STTop(&st) 获取栈顶元素（即当前区间的边界），然后 STPop(&st) 弹出栈顶元素。这里是先弹出 left，再弹出 right，也就是我们要处理的区间是 [left, right]。

分区操作：

int keyi = PartSort1(a, left, right);

调用 PartSort1(a, left, right) 对当前区间 [left, right] 进行分区。PartSort1 的作用是找到基准值 keyi 的最终位置，使得 keyi 左边的元素都小于或等于基准值，右边的元素都大于基准值。此时，基准值 a[keyi] 已经归位。

keyi 是分区后基准值所在的位置。

处理分区后的左右子区间：

if (keyi + 1 < right)
{
    STPush(&st, right);
    STPush(&st, keyi + 1);
}

if (left < keyi - 1)
{
    STPush(&st, keyi - 1);
    STPush(&st, left);
}

快速排序的核心步骤是递归或非递归地对左右子区间继续进行分区。在这里，通过栈来模拟递归的过程。对于当前区间 [left, right]，分区后会产生两个子区间：

左子区间：[left, keyi - 1]
右子区间：[keyi + 1, right]

代码中通过判断条件来决定是否需要将左右子区间压入栈：

如果 keyi + 1 < right，说明右子区间存在且需要排序，于是将右子区间 [keyi + 1, right] 的边界压入栈。
如果 left < keyi - 1，说明左子区间存在且需要排序，于是将左子区间 [left, keyi - 1] 的边界压入栈。

通过压栈操作，我们可以保证在后续的循环中，这些子区间会被进一步处理。

栈处理完毕，排序结束：

STDestroy(&st);

当栈为空时，说明所有区间都已经被处理完毕，排序完成。最后，调用 STDestroy(&st) 释放栈资源。

代码核心思想：

栈的使用： 栈用于模拟递归过程，每次处理一个区间 [left, right] 后，将左右子区间（如果存在）压入栈中，依次处理。栈顶始终保存的是当前要处理的区间。
分区操作： 通过 PartSort1 将当前区间分为左右两个子区间，然后递归处理左右子区间。
非递归实现： 非递归快速排序的关键是使用栈替代递归，使得每次分区后的左右子区间能够被依次处理，避免系统递归栈溢出的问题。

示例过程：

我们以数组 a = [3, 1, 2, 5, 4, 6, 9, 7, 10, 8] 为例：

初始栈状态为 [begin=0, end=9]。
弹出栈顶，处理区间 [0, 9]，分区后基准值为 6，将区间 [0, 5] 和 [7, 9] 压入栈。
弹出栈顶，处理区间 [7, 9]，分区后基准值为 8，将区间 [7, 7] 和 [9, 9] 不再处理。
弹出栈顶，处理区间 [0, 5]，分区后基准值为 4，将区间 [0, 3] 和 [5, 5] 不再处理。
如此反复，直到栈为空，数组最终有序。

冒泡排序

思路：左边大于右边则交换，一趟排下来最大的在右边

冒泡排序的工作原理

比较和交换：
- 从数组的开头开始，比较相邻的两个元素。
- 如果前一个元素大于后一个元素，则交换它们的位置。
- 这一步骤会将最大的元素移动到数组的末尾。
重复遍历：
- 对数组进行多次遍历，每次遍历都把下一个最大元素放到正确的位置。
- 每次遍历结束后，未排序部分的长度会减少，因为最大的元素已经在末尾。
提前终止：
- 如果在某次遍历中没有发生任何交换，说明数组已经有序，可以提前终止排序过程。

代码解析

void BubbleSort(int* a, int n) {
    for (size_t j = 0; j < n; j++) { // 外层循环，进行n次遍历
        int exchange = 0; // 用于标记是否发生交换
        for (size_t i = 1; i < n - j; i++) { // 内层循环，比较相邻元素
            // 只有在前一个元素大于后一个元素时才进行交换
            if (a[i - 1] > a[i]) {
                Swap(&a[i - 1], &a[i]); // 交换元素
                exchange = 1; // 记录有交换发生
            }
        }
        // 如果没有交换，说明已经排序完成
        if (exchange == 0) {
            break; // 提前结束
        }
    }
}

详细步骤示例

假设我们有一个数组 `[5, 3, 8, 4, 2]`，下面是冒泡排序的具体过程：

第一次遍历：
- 比较 5 和 3：5 > 3，交换 → [3, 5, 8, 4, 2]
- 比较 5 和 8：不交换 → [3, 5, 8, 4, 2]
- 比较 8 和 4：8 > 4，交换 → [3, 5, 4, 8, 2]
- 比较 8 和 2：8 > 2，交换 → [3, 5, 4, 2, 8]
- 最大元素 8 冒泡到最后。
第二次遍历：
- 比较 3 和 5：不交换 → [3, 5, 4, 2, 8]
- 比较 5 和 4：5 > 4，交换 → [3, 4, 5, 2, 8]
- 比较 5 和 2：5 > 2，交换 → [3, 4, 2, 5, 8]
- 最大元素 5 冒泡到倒数第二个位置。
第三次遍历：
- 比较 3 和 4：不交换 → [3, 4, 2, 5, 8]
- 比较 4 和 2：4 > 2，交换 → [3, 2, 4, 5, 8]
- 最大元素 4 冒泡到倒数第三个位置。
第四次遍历：
- 比较 3 和 2：3 > 2，交换 → [2, 3, 4, 5, 8]
- 由于没有其他交换，排序完成。