时间序列数据的平稳性分析

时间序列分析中，平稳性是一个关键的概念。一个平稳的时间序列在不同时间段内的统计性质保持不变，这使得能够更可靠地进行预测和建模。在本篇博客中，将介绍平稳性的理论概念、相关公式，并通过代码示例演示如何检验和实现时间序列的平稳性。

1. 理论概念

平稳性是指时间序列在时间轴上的统计性质保持不变。具体来说，一个平稳的时间序列应该满足以下两个条件：

• 常数均值：序列的均值在时间上保持不变。
• 常定方差：序列的方差在时间上保持不变。

平稳性对于时间序列分析至关重要。如果时间序列不是平稳的，我们可能会观察到趋势、季节性或其他结构，这使得预测和建模变得更加复杂。

2. 平稳性的检验

2.1 观察法

通过绘制时间序列图，我们可以初步观察序列是否具有常数均值和方差。如果序列在图中呈现出稳定的波动，可能是平稳的。然而，这种方法并不总是准确。

2.2 统计检验

常用的统计检验方法包括：

• ADF检验（Augmented Dickey-Fuller Test）：检验序列是否存在单位根（unit root），从而判断是否平稳。
• KPSS检验（Kwiatkowski-Phillips-Schmidt-Shin Test）：检验序列是否是平稳的。

这两个检验的零假设和备择假设如下：

• ADF检验的零假设 $H_0$：序列具有单位根，不平稳；备择假设 $H_1$：序列平稳。
• KPSS检验的零假设 $H_0$：序列是平稳的；备择假设$H_1$：序列具有单位根，不平稳。

3. 平稳性的公式

3.1 ADF检验的统计量

ADF检验的统计量（t统计量）的计算公式为：

$$\begin{array}{c}t=\frac{\text{观察到的单位根统计量}-\text{临界值}}{\text{标准误差}}\end{array}$$

其中，观察到的单位根统计量衡量了序列是否具有单位根，标准误差表示估计的不确定性。

3.2 KPSS检验的统计量

KPSS检验的统计量（LM统计量）的计算公式为：

$$\begin{array}{c}LM=\frac{\text{长期方差估计}}{\text{短期方差估计}}\end{array}$$

长期方差估计和短期方差估计分别表示序列的长期趋势和短期波动。

4. 代码示例

让我们通过一个简单的代码示例来演示如何检验和实现时间序列的平稳性。在这个例子中，我们将使用Python和常见的时间序列库进行操作。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller, kpss

# 创建示例时间序列数据
np.random.seed(42)
time_series = np.random.randn(100) + np.arange(100)

# 绘制时间序列图
plt.figure(figsize=(10, 6))
plt.plot(time_series)
plt.title('Example Time Series')
plt.xlabel('Time')
plt.ylabel('Value')
plt.show()

# ADF检验
adf_result = adfuller(time_series)
print(f'ADF Statistic: {adf_result[0]}')
print(f'p-value: {adf_result[1]}')
print('Critical Values:')
for key, value in adf_result[4].

items():
    print(f'   {key}: {value}')

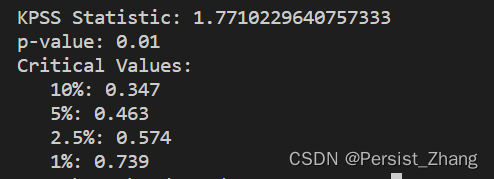
# KPSS检验
kpss_result = kpss(time_series)
print('\nKPSS Statistic:', kpss_result[0])
print('p-value:', kpss_result[1])
print('Critical Values:')
for key, value in kpss_result[3].items():
    print(f'   {key}: {value}')

在这个示例中，生成了一个简单的随机时间序列，并使用adfuller函数进行ADF检验，使用kpss函数进行KPSS检验。根据检验结果的 p-value，我们可以判断序列是否平稳。在实际应用中，我们通常会结合可视化和多个检验方法来判断序列的平稳性。

5. 总结

平稳性是时间序列分析中的一个基本概念，对于建模和预测具有重要意义。通过观察时间序列图以及进行统计检验，我们可以判断序列是否平稳。在实际应用中，根据序列的特点选择合适的检验方法，并结合多方面的分析，有助于更准确地判断和处理时间序列的平稳性。