MATLAB计算极限和微积分
求极值,一个想法是求出一阶导为0的点,不过这样需要人为判断是极大值还是极小值,以及结合单调性判断必要条件~f = @(x) x.^2 + 2*x + 1;(本质还是求极限,列出公式调用limit函数限即可,此处暂略~)的选择很重要,其实甚至可以使用遗传算法和模拟退火,不过这里是。方法不够严谨,只能根据一阶微分大致估计一下单调性变化的点~如下:最大值max、间距均可以根据实际情况做出调整~求最值,这
一.函数与极限
计算极限:lim(3*x^2/(2x+1)),x分别趋于0和1,代码如下:
syms x;
limit(3*x*x/(2*x+1),x,0)
limit(3*x*x/(2*x+1),x,1)结果分别为0和1:

1.计算双侧极限
计算极限:lim(3*x^2/(2x+1)),x分别趋于0和1,代码如下:
syms x;
limit(3*x*x/(2*x+1),x,0)
limit(3*x*x/(2*x+1),x,1)2.计算单侧极限
分别计算当x从左右两边趋向0时,1/x的极限值:
syms x;
limit(1/x,x,0,'left')
limit(1/x,x,0,'right')结果分别为负无穷和正无穷:

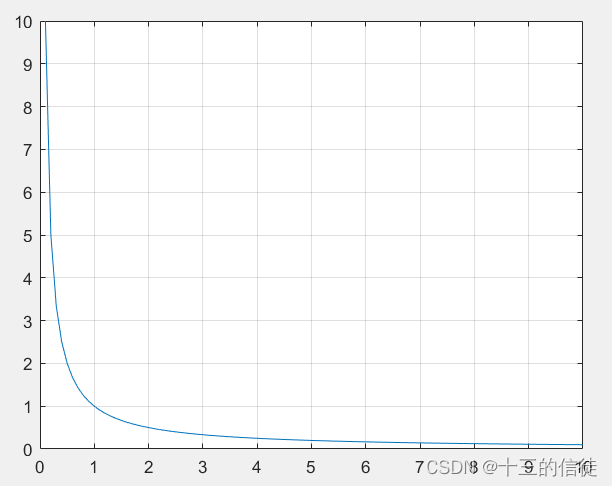
3.绘制极限图像
clear
clc
syms n
x=1/n;
y=inline(x);
max=10;
n=0:0.1:max;
figure
plot(n,y(n))
grid on
hold on如下:最大值max、间距均可以根据实际情况做出调整~

二.导数与微分
1.一阶导数
syms x
diff(sin(2*x))结果为:2cos2x

Tips:
在MATLAB中书写要严谨,sin2x要写成sin(2*x),千万不要习惯性简写~
2.高阶导数
计算:3(x^4)+4(x^2)+cos(2*x)的三阶导数:
一阶导如下:
三阶导如下:
-
syms x -
diff(3*(x^4)+4*(x^2)+cos(2*x),x,3)

3.参数方程求导
设参数方程:
- x=3*sin(2*n)
- y=arcsin(n^2)
syms n
x=3*sin(2*n)
y=asin(n^2)
diff(y)/diff(x)
%pretty(diff(y)/diff(x))
三.微分中值定理及其应用
四.不定积分
1.极值与最值
求极值,一个想法是求出一阶导为0的点,不过这样需要人为判断是极大值还是极小值,以及结合单调性判断必要条件~
syms x y
y=sin(x)+cos(2*x);
num=diff(y);
solve(num)
求最值,这里使用了内联函数,本质上还是暴力搜索,所以搜索范围和搜索间隔的选择很重要,其实甚至可以使用遗传算法和模拟退火,不过这里是考研数学,就不展开写高难度的算法了~
clear
clc
t= -100:0.0001:100;
syms x;
y = inline(x^2+5*x+12);
max = max(y(t));
min = min(y(t));(相比之下还是用极值法比较简易。。。)
2.单调区间
f = @(x) x.^2 + 2*x + 1; %函数句柄的写法
x = -10:0.1:10;
y = f(x);
dy = diff(y);%计算一阶微分
方法不够严谨,只能根据一阶微分大致估计一下单调性变化的点~
3.渐近线
(本质还是求极限,列出公式调用limit函数限即可,此处暂略~)
五.定积分
syms x y;%变量
f=sin(2*x)+3*cos(3*x)+3*x+3; %目标函数式
int(f,'x')%求解不定积分,两个参数分别为积分表达式和被积变量 (注意不定积分往往答案不唯一,若答案不一致可以尝试变形看看与自己算的结果是否一致~)
(注意不定积分往往答案不唯一,若答案不一致可以尝试变形看看与自己算的结果是否一致~)
六.定积分的应用
(基本上是一些应用题~)

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献41条内容
已为社区贡献41条内容






所有评论(0)