【MWORKS专业工具箱系列教程】控制系列工具箱第二期：控制系统模型转换

本工具箱教程以控制系统模型创建、分析与设计流程为主线，通过大量示例介绍MWORKS控制系统工具箱的功能和具体使用。本期介绍的控制系统模型转换包括两部分：模型类转换、连续离散转换。对以下形式的传递函数转化为状态空间表达式，即为系统实现。的转换称之为系统实现，反之，也可通过计算方式得到。将以下离散时间系统进行重采样，重采样时间为。上述两种形式转换的具体推导不在此赘述。将以下零极点增益模型转化为状态空间

同元软控

1490人浏览 · 2024-09-24 10:19:23

同元软控 · 2024-09-24 10:19:23 发布

本工具箱教程以控制系统模型创建、分析与设计流程为主线，通过大量示例介绍MWORKS控制系统工具箱的功能和具体使用。共计10篇文章，上一篇主要介绍了控制系统模型创建。

同元软控：【MWORKS专业工具箱系列教程】控制系列工具箱第一期：控制系统模型创建

本教程代码均可直接复制到Syslab中运行，使用教程中代码前需参照下述方法加载函数库内容：
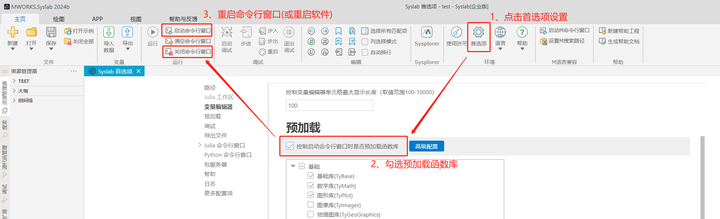
方法一：在Syslab的命令行窗口分别输入using TyControlSystems、using TyPlot并回车(重启软件或命令行窗口后需重新输入)；
方法二：按照下图中的方法预加载函数库(设置好后每次启动软件默认加载)。

第二期：控制系统模型转换

本期介绍的控制系统模型转换包括两部分：模型类转换、连续离散转换。

1. 模型类转换

系统的各种模型之间可以相互转换。

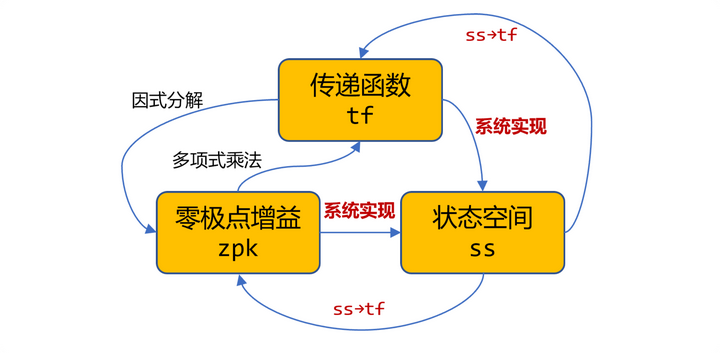
传递函数模型 tf 与零极点增益模型 zpk 之间的转换比较简单，对多项式进行处理即可。从传递函数模型 tf 到状态空间模型 ss 的转换称之为系统实现，反之，也可通过计算方式得到。

系统实现：对以下形式的传递函数转化为状态空间表达式，即为系统实现。

$G\left( s \right) = \frac{{Y\left( s \right)}}{{U\left( s \right)}} = \frac{{{b_m}{s^m} + {b_{m - 1}}{s^{m - 1}} + \cdots + {b_1}s + {b_0}}}{{{a_n}{s^n} + {a_{n - 1}}{s^{n - 1}} + \cdots + {a_1}s + {a_0}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} n \ge m$

将上述形式传递函数转化为以下的状态空间模型：

状态空间模型到传递函数的转化 ss→tf

上述两种形式转换的具体推导不在此赘述。

Syslab 中可以直接通过 tf()、ss()、zpk() 函数实现不同表达形式模型之间的相互转换

示例9：将以下状态空间模型转化为传递函数模型

output：

输入 1 到输出 1
       1.0s
-------------------
1.0s^2 + 4.0s + 5.0

输入 2 到输出 1
1.0s^2 + 5.0s + 8.0
-------------------
1.0s^2 + 4.0s + 5.0

Delay: 0.0

连续时间传递函数模型

示例10：将以下零极点增益模型转化为状态空间模型

$H\left( s \right) = \frac{{10\left( {s + 5} \right)}}{{\left( {s + 8} \right)\left( {s + 10} \right)\left( {s + 2} \right)}}$

output：

A = 
  0.0    4.0    0.0
  0.0    0.0    8.0
 -5.0  -14.5  -20.0
B = 
 0.0
 0.0
 2.0
C =
 0.78125  0.625  0.0
D =
 0.0

连续时间状态空间模型

2. 连续离散转换

Syslab支持连续-离散系统模型的相互转换，以及离散系统之间的重采样。

示例11：将以下连续模型离散化，采样时间为 ts = 0.1s

$G\left( s \right) = \frac{{s - 1}}{{{s^2} + 4s + 5}}$

output：

julia> Gd
   0.07735946566180907z - 0.08556727104741424
-------------------------------------------------
1.0z^2 - 1.6292810191076135z + 0.6703200460356392

Delay: 0.0

Sample Time: 0.1 (seconds)
离散时间传递函数模型


julia> Gd1
0.042263385959546824z^2 - 0.010930071156678337z - 0.03954112018847361
--------------------------------------------------------------------
         1.0z^2 - 1.6292810191076135z + 0.6703200460356392

Delay: 0.0

Sample Time: 0.1 (seconds)
离散时间传递函数模型

示例12：将以下离散时间系统进行重采样，重采样时间为 ts = 0.02s

$H\left( z \right) = \frac{{z - 1}}{{{z^2} + 4z + 5}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ts = 0.1s$

output：

julia> H
    1.0z - 1.0
-------------------
1.0z^2 + 1.0z + 0.3

Delay: 0.0

Sample Time: 0.1 (seconds)
离散时间传递函数模型


julia> Hc
     2.0527782215874124z - 2.052778221587414
-------------------------------------------------
1.0z^2 - 1.5169814293463761z + 0.7860030855966229

Delay: 0.0

Sample Time: 0.02 (seconds)
离散时间传递函数模型

时、频域响应对比

模型转换相关主要Syslab函数如下

函数及调用方式	说明
sys = tf(ltisys)	将ltisys系统转化为传递函数模型，ltisys可以为ss、zpk
sys = ss(ltiSys)	将ltisys系统转化为状态空间模型，ltisys可以为tf、zpk
sys = zpk(ltiSys)	将ltisys系统转化为零极点增益模型，ltisys可以为tf、ss
sysd = c2d(sysc, Ts) sysd = c2d(sysc, Ts, method)	将连续时间模型转化为离散时间模型
sysc = d2c(sysd) sysc = d2c(sysd, method)	将离散时间模型转化为连续时间模型
sys1 = d2d(sysc, Ts) sys1 = d2d(sysc, Ts, method)	对离散时间动态系统模型进行重新采样，以产生具有新采样时间 Ts (以秒为单位) 的等效离散时间模型