---

前言

计算圆周率有多种算法，其中割圆术是中国最早的一种算法，理解简单，适合入门。而随着计算机、数学的发展，人们发明了更高效的算法，计算机也帮助人们将圆周率计算至小数点后 3.14 万亿位。

---

一、割圆术简介

割之弥细，所失弥少，割之又割，以至于不可割，则与圆合体，而无所失矣。

所谓“割圆术”（cyclotomic method），是用圆内接正多边形的面积去无限逼近圆面积并以此求取圆周率的方法。
参考：百度百科——割圆术

二、原理

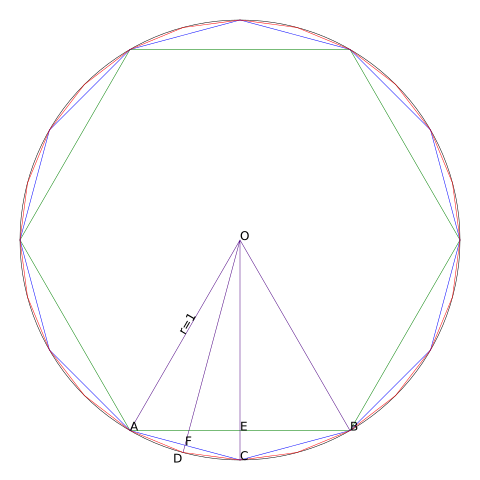
如图所示，根据圆的面积公式 $S=\pi r^2$ 可知，当圆的半径为 1 时，圆的面积等于 π，所以我们可以算半径为 1 的正多边形的面积，即可得到近似的 π。观察图像，S_圆 > S_正24边形 > S_正12边形 > S_正6边形，所以我们的计算结果的精确度随边的个数的增加而提高，但始终小于 S_圆，即始终小于 π。

三、算法实现

如图，
$S_{△AOB}=\frac{1}{2}{r}^2\sin 60^{\circ }$
$S_{△AOC}=\frac{1}{2}{r}^2\sin 30^{\circ }$
$S_{△AOD}=\frac{1}{2}{r}^2\sin 15^{\circ }$
$\dots$
$S_{△AON}=\frac{1}{2}{r}^2\sin \angle AON$，
而
$S_{正六边形}=6S_{△AOB}=3\sin 60^{\circ }=\frac{3\sqrt{3}}{2}$
$S_{正十二边形}=12S_{△AOC}=6\sin 30^{\circ }=\frac{3\sin 60^{\circ }}{\cos 30^{\circ }}$
$S_{正二十四边形}=24S_{△AOD}=12\sin 15^{\circ }=\frac{6\sin 30^{\circ }}{\cos 15^{\circ }}$
$\dots$
$S_{正3\cdot 2^n边形}=3\cdot 2^n{S}_{△AON}=3\cdot 2^{n-1}\sin \frac{60^{\circ }}{2^{n-1}}=\frac{3\cdot 2^{n-2}\sin \frac{60^{\circ }}{2^{n-2}}}{\cos \frac{60^{\circ }}{2^{n-1}}}$
我们不难发现，对于任意 $n(n\ge 1)$，有：
$$S_{正3\cdot 2^n边形}=\frac{S_{正3\cdot 2^{n-1}边形}}{\cos \frac{60^{\circ }}{2^{n-1}}}$$
记$a_n=\cos \frac{60^{\circ }}{2^{n-1}}$，则$S_{正3\cdot 2^n边形}=\frac{S_{正六边形}}{{\prod }_{i=1}^n{a}_i}$。
所以，可以先计算${\prod }_{i=1}^n{a}_i$，然后除$S_{正六边形}$
而若用cos函数计算，则要用到 π，这无异于用结论算结论。而根据半角公式，可以得出$a_n$的递推公式：
$$a_n=\sqrt{\frac{a_{n-1}+1}{2}}$$
所以程序如图：

四、实例代码

Java I

import java.util.Scanner;

public class Main {
	public static void main(String[] args){
		Scanner input=new Scanner(System.in);
		int n=input.nextInt(),i=1;
		double p=0.5,s=1;
		while(i<=n){
			p=Math.sqrt((p+1)/2);
			s=s*p;
			i++;
		}
		System.out.println(1.5*Math.sqrt(3)/s);
	}
}

结果：

99
3.141592653589794

Java II

该处使用了 java.math.BigDecimal 模块，以提高小数位数。

import java.math.BigDecimal;
import java.math.MathContext;
import java.math.RoundingMode;
import java.util.Scanner;

public class Main {
	static MathContext mc = new MathContext(100, RoundingMode.HALF_UP); 		
	//BigDecimal开方
	public static BigDecimal sqrt(BigDecimal a) {
		BigDecimal _2=BigDecimal.valueOf(2.0);
		if(a.compareTo(BigDecimal.ZERO)==0)return BigDecimal.ZERO;
		else{
			BigDecimal x=a;
			int cnt=0;
			while(cnt<100){
				x=(x.add(a.divide(x,mc))).divide(_2,mc);
				cnt++;
			}
			return x;
		}
	}

	public static void main(String[] args){
		Scanner input=new Scanner(System.in);
		int n=input.nextInt(),i=1;
		BigDecimal p=new BigDecimal("0.5"),s=BigDecimal.ONE;
		while(i<=n){
			p=sqrt(p.add(BigDecimal.ONE).divide(new BigDecimal("2"),mc));
			s=s.multiply(p);
			i++;
		}
		System.out.println(sqrt(new BigDecimal("3")).multiply(new BigDecimal("1.5")).divide(s,mc));
	}
}

结果：（该算法精确至小数点后60位）

100
3.141592653589793238462643383279502884197169399375105820974944/*第60位*/234988309941294683211597479745467855302

Python

该处用到了 decimal 库，精确度更高。

#!/usr/bin/python3
# -*- coding: utf-8 -*-
from decimal import *
getcontext().prec=256 #数字长度
n,i,c,s=input('请输入n: '),0,Decimal('0.5'),Decimal('1')
n=int(n)
while i<n:
	c=((c+1)/2)**Decimal('0.5')
	s*=c
	i+=1
print('π约为: '+str(Decimal('1.5')*(Decimal('3')**Decimal('0.5'))/s))

结果：（该算法精确至小数点后 253 位）

请输入n: 1024
π约为: 3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446095505822317253594081284811174502841027019385211055596446229489549303819644288109756659334461284756482337867831652712019091456/*第253位*/50

---

总结

文章结束，你应该掌握了割圆术，运用数学上的极限思维解决问题。对于圆周率的计算，目前已没多大实用意义，但这正是计算机技术进步的一个标尺。

声明：未经作者允许禁止转载。