参考书目：《神经计算建模实战——基于brainpy》 吴思

0.引言 

        上一篇笔记中的HH模型可以精准刻画离子通道的开启与关闭，从而模拟动作电位的产生细节。其缺点在于当需要模拟动作电位发放细节时，HH模型需要较小的数值积分步长，并且其变量较多，计算代价较大。

        从更宏观的角度上来看，我们模拟神经网络时，往往更加关注一个神经元对其他神经元的影响，因此细致模拟膜电位变化过程是非必要的。因此，在模拟大规模神经网络时，需要重新引入一些简化的神经元模型。本文从最基础的泄露整合发放LIF模型出发，介绍一些简化模型（包括二次整合发放QIF模型、指数整合发放ExpIF模型、适应性指数整合发放AdEx模型、Izhikevich模型、Hindmarsh-Rose模型、泛化整合发放GIF模型）以及brainpy代码实现。

1.泄露整合发放LIF模型

1.1 LIF模型定义

        LIF模型将细胞膜简化为单通道电路，在达到膜电位阈值前，神经元的膜电位主要由泄露通道调控，泄露通道的电阻可被建模为常值R。神经元的静息电位为V_{rest}，神经元脉冲发放的膜电位阈值为V_{th}，神经元产生脉冲后的重置膜电位为V_{reset}，不应期时长为t_{ref}（最初的LIF模型没有考虑不应期），接受输入电流I(t)。当膜电位超过阈值V_{th}，神经元发放脉冲，之后进入不应期，此时膜电位不发生变化。其等效电路图如下：

 根据基尔霍夫定律和电位发放规律，列出LIF模型的数学表达式如下：

\left\{\begin{matrix} \tau\frac{dV}{dt}=-(V-V_{rest})+RI(t) \\ \text{if}\quad V>V_{th},\quad V\leftarrow V_{reset}\quad \text{last}\quad t_{ref} \end{matrix}\right.

        第一个等式中的\tau=RC表示模型的时间常数，越大则模型的动力学变化越慢。

1.2 LIF模型的代码实现

利用brainpy编程如下：

import brainpy as bp
import brainpy.math as bm
import numpy as np
import matplotlib.pyplot as plt

class LIF(bp.dyn.NeuGroup):
    def __init__(self,size,V_rest=0.,V_reset=-5.,V_th=20.,R=1.,tau=10.,t_ref=5.,name=None):
        super(LIF,self).__init__(size=size,name=name)

        #初始化参数
        self.V_rest = V_rest
        self.V_reset = V_reset
        self.V_th = V_th
        self.R = R
        self.tau = tau
        self.t_ref = t_ref

        #初始化变量
        self.V = bm.Variable(bm.random.randn(self.num) + V_reset)
        self.input = bm.Variable(bm.zeros(self.num))
        self.t_last_spike = bm.Variable(bm.ones(self.num)* -1e7) #上一次脉冲发放时刻
        self.refractory = bm.Variable(bm.zeros(self.num,dtype=bool)) #是否处于不应期
        self.spike = bm.Variable(bm.zeros(self.num,dtype=bool)) #脉冲发放状态

        #积分函数
        self.integral = bp.odeint(f=self.derivative,method='exp_auto')

        #定义膜电位关于时间变化的微分方程
    def derivative(self,V,t,R,Iext):
        dvdt = (-V + self.V_rest + R * Iext) / self.tau
        return dvdt

        #更新函数
    def update(self,tdi):
        t,dt = tdi.t,tdi.dt
        refractory = (t - self.t_last_spike) <= self.t_ref #是否处于不应期
        V = self.integral(self.V,t,self.R,self.input,dt=dt) #根据时间步长更新膜电位
        V = bm.where(refractory,self.V,V)
        spike = V>self.V_th #更新脉冲状态
        self.spike.value = spike
        self.t_last_spike = bm.where(spike,t,self.t_last_spike) #更新上次脉冲时间
        self.V.value = bm.where(spike,self.V_reset,V)
        self.refractory.value = bm.logical_or(refractory,spike)
        self.input[:]=0#重置外界输入

初始化一个LIF模型并进行数值模拟，外界输入电流恒定为20.5mA，模拟时长200ms，利用DSRunner运行：

group = LIF(1)
runner = bp.dyn.DSRunner(group,monitors=['V'],inputs=('input',20.5))
#外界输入电流恒定为20.5mA
runner(200)

plt.plot(runner.mon.ts,runner.mon.V)
plt.xlabel('t(ms)')
plt.ylabel('V')
plt.show()

输出结果如图：

        由图可知，LIF模型并不能模拟真实情况下动作电位的形状。在发放动作电位前，LIF 神经元膜电位的增长速度将逐渐降低，并非像真实神经元那样先缓慢增长，在达到一定值之后转为迅速增长。之后介绍的QIF模型针对此缺陷进行了改进。

1.3 LIF模型的其他性质

        根据LIF模型，可解出其数学表达式，由此可知当电流强度I大于引发神经元膜电位到达阈值电位V_{th}的基强度电流I_\theta=\frac{V_{th}-V_{reset}}{R}时，才能产生动作电位。在此例中I_\theta=20，即输入电流需超过20才能产生动作电位，不信的话，可以试试。

        试试就试试：

duration = 200
neu1 = LIF(1,t_ref=5.)
neu1.V[:] = bm.array([-5.]) #   V初始值
runner = bp.dyn.DSRunner(neu1,monitors=['V'],inputs=('input',20))
runner(duration)
plt.plot(runner.mon.ts,runner.mon.V,label=r'$I=20$')

neu2 = LIF(1,t_ref=5.)
neu2.V[:] = bm.array([-5.]) #   V初始值
runner = bp.dyn.DSRunner(neu2,monitors=['V'],inputs=('input',20.1))
runner(duration)
plt.plot(runner.mon.ts,runner.mon.V,label=r'$I=20.1$')

neu3 = LIF(1,t_ref=5.)
neu3.V[:] = bm.array([-5.]) #   V初始值
runner = bp.dyn.DSRunner(neu3,monitors=['V'],inputs=('input',19.9))
runner(duration)
plt.plot(runner.mon.ts,runner.mon.V,label=r'$I=19.9$')

neu4 = LIF(1,t_ref=5.)
neu4.V[:] = bm.array([-5.]) #   V初始值
runner = bp.dyn.DSRunner(neu4,monitors=['V'],inputs=('input',19))
runner(duration)
plt.plot(runner.mon.ts,runner.mon.V,label=r'$I=19$')

neu5 = LIF(1,t_ref=5.)
neu5.V[:] = bm.array([-5.]) #   V初始值
runner = bp.dyn.DSRunner(neu5,monitors=['V'],inputs=('input',21))
runner(duration)
plt.plot(runner.mon.ts,runner.mon.V,label=r'$I=21$')

plt.xlabel('t(ms)')
plt.ylabel('V')
plt.legend()
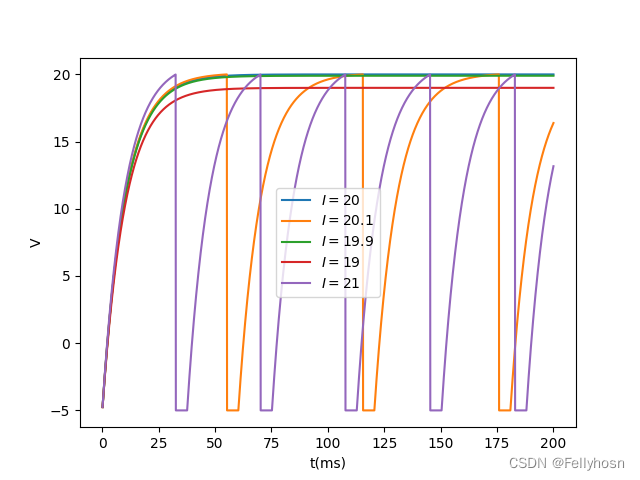
plt.show()

试试的结果如下：

        当输入电流＜20时，不产生动作电位，大于20产生动作电位。强度为 20 的电流不能激发动作电位，因为此时神经元的膜电位随时间无限逼近但并不能达到V_{th}

2 二次整合发放（QIF）模型

2.1 QIF模型定义

        为了弥补LIF模型在动作电位上的表征缺陷，Latham等人提出了二次整合发放模型（Quadratic Integrate-and-Fire model），其微分方程的二阶项更好地模拟了动作电位：

\left\{\begin{matrix} \tau\frac{dV}{dt}=a_0(V-V_{rest})(V-V_c)+RI(t) \\ \text{if}\quad V>\theta,\quad V\leftarrow V_{reset}\quad \text{last}\quad t_{ref} \end{matrix}\right.

，其中a_0>0,V_c>V_{rest}

        与LIF模型的方程相比，QIF模型的第一个式子右侧是关于V的二次方程，即代表膜电位的上升由慢变快。V_c代表神经元的兴奋阈值，a_0控制了神经元的发放频率和发放前膜电位增长速度。当膜电位达到峰值\theta后，膜电位被重置为V_{reset}，代码如下：

import brainpy as bp
import brainpy.math as bm
import numpy as np
import matplotlib.pyplot as plt

class QIF(bp.dyn.NeuGroup):
    def __init__(self,size,V_rest=-65.,V_reset=-68.,V_th=-30.,V_c=-50.0,a_0=.07,R=1.,tau=10.,t_ref=5.,name=None):
        super(QIF,self).__init__(size=size,name=name)

        #初始化参数
        self.V_rest = V_rest
        self.V_reset = V_reset
        self.V_th = V_th
        self.V_c =V_c
        self.a_0 = a_0
        self.R = R
        self.tau = tau
        self.t_ref = t_ref

        #初始化变量
        self.V = bm.Variable(bm.random.randn(self.num) + V_reset)
        self.input = bm.Variable(bm.zeros(self.num))
        self.t_last_spike = bm.Variable(bm.ones(self.num)* -1e7) #上一次脉冲发放时刻
        self.refractory = bm.Variable(bm.zeros(self.num,dtype=bool)) #是否处于不应期
        self.spike = bm.Variable(bm.zeros(self.num,dtype=bool)) #脉冲发放状态

        #积分函数
        self.integral = bp.odeint(f=self.derivative,method='exp_auto')

        #定义膜电位关于时间变化的微分方程
    def derivative(self,V,t,Iext):
        dvdt = (self.a_0 * (V-self.V_rest) * (V-self.V_c) + self.R * Iext) /self.tau
        return dvdt

        #更新函数
    def update(self,tdi):
        t,dt = tdi.t,tdi.dt
        refractory = (t - self.t_last_spike) <= self.t_ref #是否处于不应期
        V = self.integral(self.V,t,self.input,dt=dt) #根据时间步长更新膜电位
        V = bm.where(refractory,self.V,V)
        spike = V>self.V_th #更新脉冲状态
        self.spike.value = spike
        self.t_last_spike = bm.where(spike,t,self.t_last_spike) #更新上次脉冲时间
        self.V.value = bm.where(spike,self.V_reset,V)
        self.refractory.value = bm.logical_or(refractory,spike)
        self.input[:]=0#重置外界输入

group = QIF(1)
runner = bp.dyn.DSRunner(group,monitors=['V'],inputs=('input',8.)) #恒定电流8mA
runner(500) #500ms

plt.plot(runner.mon.ts,runner.mon.V)
plt.ylabel('V')
plt.show()

        输出结果：可以看到动作电位时，V的上升由慢变快

 2.2 QIF模型的基强度电流

        根据QIF的微分方程可求出本例中基强度电流为3.94

模拟不同的输入电流：

duration=500
group1 = QIF(1)
runner = bp.dyn.DSRunner(group1,monitors=['V'],inputs=('input',5.))
runner(duration)
plt.plot(runner.mon.ts,runner.mon.V,label=r'$I=5.$')

group2 = QIF(1)
runner = bp.dyn.DSRunner(group2,monitors=['V'],inputs=('input',4.))
runner(duration)
plt.plot(runner.mon.ts,runner.mon.V,label=r'$I=4.$')

group3 = QIF(1)
runner = bp.dyn.DSRunner(group3,monitors=['V'],inputs=('input',3.))
runner(duration)
plt.plot(runner.mon.ts,runner.mon.V,label=r'$I=3.$')

group4 = QIF(1)
runner = bp.dyn.DSRunner(group4,monitors=['V'],inputs=('input',2.))
runner(duration)
plt.plot(runner.mon.ts,runner.mon.V,label=r'$I=2.$')

plt.xlabel('t(ms)')
plt.ylabel('V(mV)')
plt.legend()
plt.show()

得到图像如下：

 2.3 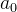a_0对QIF模型的影响

        理论推导如下：

         在之前的例子中，可以求得a_0 \in (0,0.089)，下面测试a_0的取值对QIF神经元发放频率及发放曲线的影响：

duration = 600
group1 = QIF(1,a_0=0.005)
runner = bp.dyn.DSRunner(group1,monitors=['V'],inputs=('input',5.))
runner(duration)
plt.plot(runner.mon.ts,runner.mon.V,label=r'$a0=0.005$')

group2 = QIF(1,a_0=0.045)
runner = bp.dyn.DSRunner(group2,monitors=['V'],inputs=('input',5.))
runner(duration)
plt.plot(runner.mon.ts,runner.mon.V,label=r'$a0=0.045$')

group3 = QIF(1,a_0=0.085)
runner = bp.dyn.DSRunner(group3,monitors=['V'],inputs=('input',5.))
runner(duration)
plt.plot(runner.mon.ts,runner.mon.V,label=r'$a0=0.085$')

plt.xlabel('t(ms)')
plt.ylabel('V(mV)')
plt.legend()
plt.show()

 测试结果如下：随着a_0的增长，神经元发放频率先增加后降低，阈下膜电位变化曲线从平滑上升变为先缓慢上升，后急速上升。因此a_0不仅影响了 QIF 模型的发放频率，还刻画了膜电位的上升曲线。

 2.4 \theta神经元模型

        QIF模型的微分方程可以通过数学推导转化为更简洁的形式，得到\theta神经元模型，其与t_{ref}=0,\theta\rightarrow \infty,V_{reset}\rightarrow -\infty的QIF模型等价，其方程为：

\frac{d\theta}{dt}=-\cos\theta+(1+\cos\theta)(2c+1/2+2bI(t))

# 学习 # 神经网络 # python
Logo
开放原子开发者工作坊

开放原子开发者工作坊旨在鼓励更多人参与开源活动，与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动，如meetup、训练营等，主打技术交流，干货满满，真诚地邀请各位开发者共同参与！

更多推荐

第二届开放原子大赛首批创新成果集结武汉，诚邀广大开发者共鉴开源技术盛宴

第二届开放原子大赛首批创新成果集结武汉，诚邀广大开发者共鉴开源技术盛宴

avatar 开放原子开发者工作坊

诚邀报名 | 开源基础设施能力建设分论坛：打造开源生态的“心脏”

诚邀报名 | 开源基础设施能力建设分论坛：打造开源生态的“心脏”

avatar 开放原子开发者工作坊

诚邀报名 | 编程语言分论坛：AI时代的技术革新与开源实践

诚邀报名 | 编程语言分论坛：AI时代的技术革新与开源实践

avatar 开放原子开发者工作坊