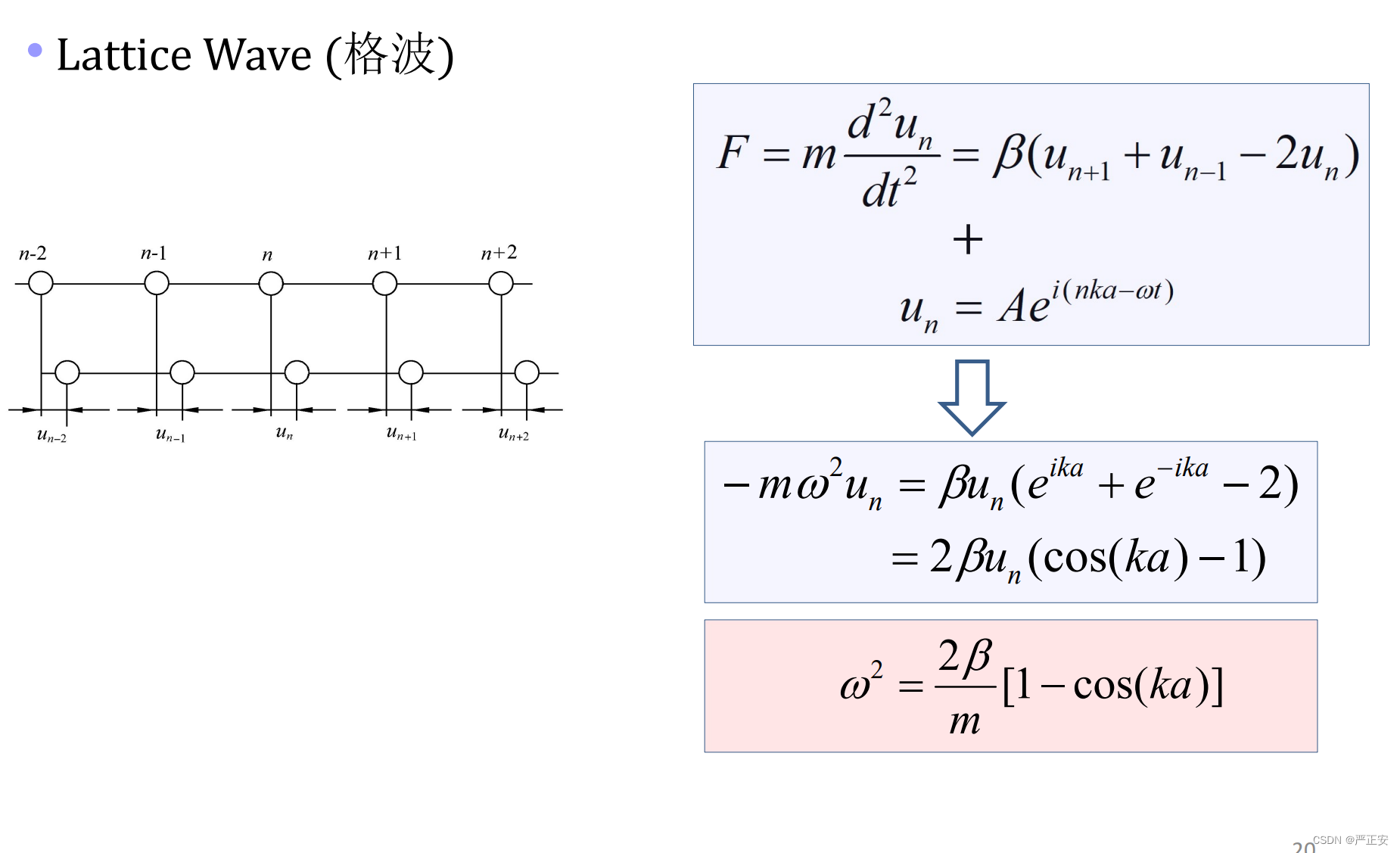
固体物理一维单原子链

固体物理

严正安

6153人浏览 · 2022-10-07 08:51:21

严正安 · 2022-10-07 08:51:21 发布

回顾：

最近邻近似，波恩冯卡曼边界条件

以所有Atom作为一个周期，所有原子都是在一个环形的链条里面，只是周长特别长，不会妨碍一维单原子链的整体性质

一维单原子链，我们主要是研究纵向，我们只是画出了大小，方向还是沿着这一条链

对于不同的晶体来说 $\small U$ 不同， $\small \beta$ 也不同，但是在平衡位置处附近 $\small \beta$ 是一个常数

最终得到的是

这是我们遇到的第一个色散关系

色散关系讲的是波的传播随频率变化的一个关系， $\small \omega$ 是频率

我们有三角函数可以得到第一布里渊区的概念，我们在倒格空间中，在原点附近，以原点作为中心，一个倒格矢长度的范围 $\small a->\frac{2\pi}{a}$

我们把一维的中心定义为0，左右对称，画出了 $\small [-\frac{\pi}{a} \sim \frac{\pi}{a} ]$ ，定义为第一布里渊区

我们对于色散关系， $\small \omega \sim k$ 的关系

$\small \nu =\frac{\omega}{k}=\frac{2}{k}\sqrt{\frac{\beta}{m}|sin(\frac{ka}{2})|}$ 相速度， $\small \frac{d\omega}{dk}$ 群速度

我们说的速度不能超过光速，指的是群速度不超过光速，群速度是能量传播的速度

我们可以从斜率看出，群速度一致在变化

色散关系的特点就是，不同频率的波速度不一样

eg：我们在光纤中，我们想要网速快（除了真空，任何物质都有色散），不同频率的光在光纤中的速度是不一样的，这个色散可以非常不显著，如果从美国走到中国，非常小的速度差，也可以有延迟，画面就变得非常卡顿，随着就距离增大，时间就发生了变化，这是色散一个相对容易理解的

一个近似，我们就可以消去 $\small \sin$

这样的话，我们就可以得到一个不关于K的一个速度，是一个常数

这就意味着在趋近于0的时候，他的速度没有变化，当 $\small k->0$ ，速度不发变化

k趋向于0，如果我们用 $\small \lambda$ 表示，那么 $\small \lambda$ 趋向于无穷大，我们叫他长波极限，波长非常的长，波长趋近于无穷大，如果我的晶体是一个粉笔的长度，波长无穷大，穿过它的时间也会非常快，它对于波长来讲是微乎其微的，他可能只是波长里的一个小点（相对于无穷大来讲),也就是说在这个长波穿过这个晶体的时候，这个波长可以轻而易举地穿过这个晶体，因为不用引起晶体中复杂原子地运动，这个晶体中所有原子会以几乎相同的运动方式，以这个长波长地波在运动，对于波长来讲，原子的范围太小，所有的原子看作一个点，运动是相同的

从位移的一般公式，我们也可以看出来

所有的Atom都是相同的运动方式，相位差需要用ka来代表他，ka=0

这样的话在k趋向于0的时候，波长远远大于a，因此就可以看作是一种elastic wave(弹性波)

与弹性波相对应的是非弹性波，弹性波的含义是波经过他之后，对这个晶格来说，感觉没有传递任何有效的信息和能量，从另一个角度来讲，lattice wave 穿过晶体的时候，非常的自由，如果有碰撞说不定就有能量的传递，在穿过晶体的时候，是自由的透明的，然后就可以完全穿过这个晶体（在穿过晶体的时候，没有产生任何的反应），这是长波传递下的传播特点（所有原子就像一个非常小的小点），我们从sin函数在 $\small [-\frac{\pi}{a} \sim \frac{\pi}{a}]$ 看出，是有最大值的， $\small \omega$ 也是有最大值的，对应的K就是 $\small \frac{\pi}{a}$ ，我们把 $\small k=\frac{\pi}{a}$ 代入，得出 $\small \omega_{max}=2\sqrt{\frac{\beta}{m}}$

如果频率大于一定数目的时候，好像没有色散关系了（很神奇），这一段是格波不能存在的情况，就是对一个机械波来说，这种机械运动的波，高于一定频率的时候，不工作了，不存在了，如果一个波频率高于 $\small 2\sqrt{\frac{\beta}{m}}$ ，那么就不能通过单原子链传播（他会把高频率的波的能量给全部损耗掉）

我们把不允许传播的频带称作禁带

$\small \omega_{MAX}=2\sqrt{\frac{\beta}{m}}$ ，高于这个范围不能传播和运动

我们在半导体物理中已经提到了价带，导带，禁带，已经初步提到了这个词，在半导体物理中禁带的含义是禁止电子运动的带，此处指的是禁止格波运动的带，色散关系不仅对于格波来说是这个样子，对于电子也是同样的定义，禁带的含义都相同，只是考察的对象是什么

在一维单原子链这个形式里面，这个禁带代表的是格波，也可以说是不存在的

不存在频率大于该值的格波，最大的频率我们叫它 cutoff frequency(截止频率)

举一个简单的例子：光纤传播的时候，光要在这个里面传播，是全反射的形式，不同粗细截止频率是不同的，可以传播不可以传播的颜色是不一样的

选取合适的原子质量可能对相关研究，产生很好的效果，我们还是用位移的一般解，

$\small \mu_n$ 与 $\small \mu_{n+1}$ 之间的关系，相邻的两个原子之间，运动的大小相同，方向相反，那对于 $\small k->\frac{\pi}{a}$ ，他们之间的运动，与之前相邻两个原子之间通向运动的形式相反，任意相邻的原子，在 $\small k->\frac{\pi}{a}$ ，运动都是相反方向的，形成了一种特殊的格波形式

我们把 $\small k->\frac{\pi}{a}$ ，称为短波极限

波长比较容易算出来， $\small \frac{\pi}{a}=\frac{2\pi}{\lambda} , \lambda=2a$ ,这个是我们在说的第二个特殊点，这是我们的第二个关心点

其实我们还是可以从 $\small \omega \sim k$ 的色散关系中，我们可以看出沿着k变化的，速度会趋向于0，在趋向于 $\small \frac{\pi}{a}$ 的时候，就传不动了

在k趋向于0的时候，斜率最大，群速度最大，能量传播也是最容易的，K逐渐增大，群速度逐渐减小，这个群速度就几乎为0了，格波的能量就不能够很容易传播了，几乎就不传播了，这个是一维单原子链，色散关系的第三个特点

特点回顾：1.长波极限 2.短波极限截止频率 3。群速度的变化，这是色散关系的三个特征

下面开始第四个特征

我们知道一维单原子链中，我们用了波恩冯卡曼边界条件，第un个原子的位移，应该和un+N个原子相同，我们就可以得出 $\small Nka=2\pi l$ ,l是整数， $\small k=\frac{2 \pi l}{Na}$ ,在第一布里渊区里面，把k代入，我们也可以得到l的一个取值，l的一个取值，这样的话我们就引入了一个新的物理量，l对应的一个物理量，这个l我们定义为模式数（mode number），一种波动形式就叫做一个mode，这种波动形式是一个共振的形式，也就是说不同的Atom之间会有不同的关系，共同的振动，模式是一个比较抽象的概念，是一种振动形式，这种振动是一种共振的形式，如果想比较形象化的理解这个模式，我们在机械波振动的时候，其实是有比较好的例子，比如说我们在声音的传播过程中，我们都听说过回音壁，就是一种支持多种波动形式这么一个声音的一个共振的地方，我们可以画一下这个回音壁，简单的回音壁就是圆形围墙，一个人对着墙说话，人为什么可以听到呢，是因为声音沿着波动形式传过去了，简单的理解，声音的能量会一圈一圈向外传播，知道传到整个的这个墙壁上，能量是以这种形式向外传播的，声音的共振腔中，能量是一点点往外传的，不同的人频率都是不相同的，如果再换一个声音更低沉的人，能量传递模式就会有细微的改变，模式会随着波长变化而变化，一维单原子链中，K的取值不是连续的，是一个又一个点，当然这个点非常密集，N非常大，我们可以画无穷多个点，如果我么能近距离看一下，每一个点都是不连续的，K的取值不是连续的，这个是格波的特点，1他能传递的波的频率并不是连续的，虽然可以十分接近连续，但是从数学意义上来说，是不连续的

在布里渊区我们可以找N个K的点，当然也可以说我们只看一半从 $\small 0 \sim \frac{\pi}{a}$ ,我们可以找到 $\small \frac{N}{2}$ 个点， $\small \frac{N}{2}$

个波长，如果我们懂了这一点，以后我们在看到模式数的话，我们可以从k和 $\small \lambda$ 去理解，因为模式数可k和 $\small \lambda$ 是一一对应的，在老师课题组中，设置一些光学共振结构，支持的模式数都是客户以数出来的

这就是色散关系的第四个特点，模式数是可以测出来的，测量的时候，就可以看到

测得时候一般用的是能量，能量最大的时候，可能就是一个模式，模式的最大特点还是在传递能量，用 $\small k$ 和 $\small \lambda$ 都可以，频率和能量之间的关系图，我们称之为频谱图，如果是在光学波段进行的频谱图，我们又可称之为光谱图，频谱图是电子工程中用的，我们在频谱图里面如何去看模式呢，相当于我给一系列的波长和能量，让它去传递，如果能量给它之后，系统反馈出来之后，能被他完全吸收掉，那就说明在这个波长下，它发生了一个共振，他把我的能量吸走了，此时我就知道共振频率