Stack类:常见方法讲解、使用场景、底层实现及算法问题
Stack`类是 Java 集合框架中的一个经典类,用于实现后进先出(LIFO, Last In First Out)数据结构。本文将通过深入分析 Stack的常见方法、使用场景、底层数据结构实现逻辑,并结合常见的算法问题进行讲解。
Stack 类是 Java 集合框架中的一个经典类,用于实现后进先出(LIFO, Last In First Out)数据结构。虽然 Stack 类作为一种直接的堆栈实现存在,但在开发中,Deque 或 LinkedList 更常被推荐用于堆栈的实现。不过,Stack 类仍然是一个重要的基础类,特别是在教学和理解算法设计时。
本文将通过深入分析 Stack 的常见方法、使用场景、底层数据结构实现逻辑,并结合常见的算法问题进行讲解。
1. 什么是 Stack 类?
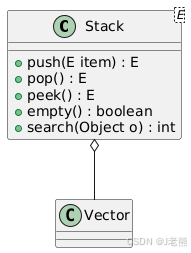
Stack 类是一种继承自 Vector 的数据结构,提供了典型的堆栈操作,如 push、pop、peek、empty 和 search。作为 LIFO 的代表,Stack 主要用于处理需要后进先出的场景。
public class Stack<E> extends Vector<E> {
public Stack() {
}
public E push(E item) {
addElement(item);
return item;
}
public synchronized E pop() {
E obj;
int len = size();
obj = peek();
removeElementAt(len - 1);
return obj;
}
public synchronized E peek() {
int len = size();
if (len == 0)
throw new EmptyStackException();
return elementAt(len - 1);
}
public boolean empty() {
return size() == 0;
}
public synchronized int search(Object o) {
int i = lastIndexOf(o);
if (i >= 0) {
return size() - i;
}
return -1;
}
}
上面的代码展示了 Stack 类的基本实现,主要是通过继承 Vector 类来管理存储的数据。
2. 常见方法讲解
2.1 push(E item)
将元素 item 压入堆栈顶部。
底层实现: Stack 类继承了 Vector,而 Vector 本质上是一个动态数组,push 方法调用 Vector 的 addElement() 方法,将新元素追加到数组末尾。
示例:
Stack<Integer> stack = new Stack<>();
stack.push(10);
stack.push(20);
stack.push(30);
在这个示例中,stack 存储了 10, 20 和 30,30 位于栈顶。
2.2 pop()
移除并返回堆栈顶部的元素。如果堆栈为空,则抛出 EmptyStackException。
底层实现: pop() 方法首先调用 peek() 获取栈顶元素,然后移除最后一个元素,使用 removeElementAt()。
示例:
int top = stack.pop(); // 返回并移除30
2.3 peek()
仅返回栈顶元素,但不移除。
底层实现: peek() 直接返回 Vector 的最后一个元素。
示例:
int top = stack.peek(); // 返回30,但不移除
2.4 empty()
判断堆栈是否为空,若为空则返回 true,否则返回 false。
2.5 search(Object o)
查找对象 o 在栈中的位置,位置是以 1 为基准的,栈顶元素位置为 1。如果未找到,返回 -1。
示例:
int pos = stack.search(20); // 返回2,因为20在栈顶的下面
3. 类图

4. 底层数据结构实现逻辑
Stack 类继承了 Vector,因此它的底层数据结构是一个动态数组。当数组容量不足时,Vector 会自动扩展容量,具体的扩展方式是每次扩展原容量的两倍。这样的设计虽然简单,但在并发场景下,由于 Vector 的所有方法都带有 synchronized,性能会受到一定影响。因此,在多线程环境中使用 Stack 类可能不是最佳选择,推荐使用 ConcurrentLinkedDeque 或 BlockingQueue。
5. 常见 Stack 相关的算法问题
5.1 括号匹配问题
问题描述: 给定一个包含括号的字符串,判断括号的匹配是否合法。
示例: 输入:"({[]})"
输出:true
解决方式: 使用堆栈存储左括号,当遇到右括号时,弹出栈顶元素并检查是否匹配。
public boolean isValid(String s) {
Stack<Character> stack = new Stack<>();
for (char c : s.toCharArray()) {
if (c == '(' || c == '{' || c == '[') {
stack.push(c);
} else {
if (stack.empty()) return false;
char top = stack.pop();
if ((c == ')' && top != '(') ||
(c == '}' && top != '{') ||
(c == ']' && top != '[')) {
return false;
}
}
}
return stack.empty();
}
5.2 栈排序问题
问题描述: 给定一个栈,将栈中的元素按升序排序,只能使用一个额外的栈作为辅助存储。
解决方式: 利用两个栈,一个栈负责存储排序后的元素,另一个栈用于暂时存放未排序的元素。
public Stack<Integer> sortStack(Stack<Integer> stack) {
Stack<Integer> sortedStack = new Stack<>();
while (!stack.empty()) {
int temp = stack.pop();
while (!sortedStack.empty() && sortedStack.peek() > temp) {
stack.push(sortedStack.pop());
}
sortedStack.push(temp);
}
return sortedStack;
}
5.3 回溯算法
问题描述: 回溯算法是一种用于解决需要搜索所有可能解决方案的问题的算法技术,尤其是在遇到迷宫、数独、八皇后等问题时常常使用。回溯算法的本质是通过不断地尝试和撤销选择,以找到问题的解决方案。在这个过程中,堆栈是一种理想的结构来存储状态信息,以便于恢复之前的状态。
在电商交易系统中,回溯算法可以用于解决复杂的订单路径规划问题,例如计算多个配送员的配送路径、根据优先级和时间窗口调整订单的最佳配送路径等。
示例:迷宫求解问题
假设有一个二维迷宫,我们需要找到从起点 (0, 0) 到终点的路径。迷宫中可能有障碍物,机器人只能上下左右移动。
class Position {
int x, y;
public Position(int x, int y) {
this.x = x;
this.y = y;
}
}
public class MazeSolver {
private static final int[][] DIRECTIONS = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
private int[][] maze;
private boolean[][] visited;
public MazeSolver(int[][] maze) {
this.maze = maze;
this.visited = new boolean[maze.length][maze[0].length];
}
public boolean solveMaze() {
Stack<Position> path = new Stack<>();
path.push(new Position(0, 0));
while (!path.empty()) {
Position current = path.pop();
// 判断是否到达终点
if (isGoal(current)) {
System.out.println("找到了解决路径!");
return true;
}
// 标记当前点为已访问
visited[current.x][current.y] = true;
// 遍历四个方向,查找未访问的相邻点
for (int[] direction : DIRECTIONS) {
int newX = current.x + direction[0];
int newY = current.y + direction[1];
if (isValid(newX, newY)) {
path.push(new Position(newX, newY));
}
}
}
System.out.println("没有找到路径!");
return false;
}
private boolean isGoal(Position position) {
return position.x == maze.length - 1 && position.y == maze[0].length - 1;
}
private boolean isValid(int x, int y) {
return x >= 0 && x < maze.length && y >= 0 && y < maze[0].length && maze[x][y] == 0 && !visited[x][y];
}
public static void main(String[] args) {
int[][] maze = {
{0, 1, 0, 0, 0},
{0, 1, 0, 1, 0},
{0, 0, 0, 1, 0},
{1, 1, 1, 1, 0},
{0, 0, 0, 0, 0}
};
MazeSolver solver = new MazeSolver(maze);
solver.solveMaze();
}
}
解决方式:
- 堆栈的使用: 每次移动时,将当前位置压入堆栈,当找到一个死路时,通过
pop()操作回溯到上一个位置。 - 时间复杂度: 由于每个位置最多访问一次,时间复杂度为 O(n),其中 n 是迷宫格子的数量。
- 适用场景: 在电商系统中,该方法可以用于寻找订单路径规划中的最优路线。
5.4 表达式求解
问题描述: 表达式求解是计算机科学中的经典问题,尤其是中缀表达式转后缀表达式以及后缀表达式求值。这类问题常用于计算器程序、编译器等领域。
示例:中缀表达式转后缀表达式
中缀表达式是一种操作符位于操作数中间的表达方式,例如 2 + 3 * 4。为了简化计算,我们通常将中缀表达式转换为后缀表达式(如 2 3 4 * +)。后缀表达式没有运算符优先级问题,可以直接从左到右求值。
使用堆栈进行中缀表达式的转换是非常高效的,主要步骤如下:
- 遇到操作数时,直接输出。
- 遇到操作符时,比较它与栈顶操作符的优先级,若栈顶优先级较高或相等,则弹出栈顶操作符并输出,直到栈顶优先级较低或栈为空。
- 遇到左括号时,直接压栈。
- 遇到右括号时,弹出栈顶操作符,直到遇到左括号为止。
解决方式:
import java.util.Stack;
public class InfixToPostfix {
// 判断是否为操作符
private static boolean isOperator(char ch) {
return ch == '+' || ch == '-' || ch == '*' || ch == '/';
}
// 获取操作符的优先级
private static int getPriority(char operator) {
if (operator == '+' || operator == '-') {
return 1;
} else if (operator == '*' || operator == '/') {
return 2;
}
return 0;
}
public static String infixToPostfix(String expression) {
Stack<Character> stack = new Stack<>();
StringBuilder result = new StringBuilder();
for (char ch : expression.toCharArray()) {
if (Character.isLetterOrDigit(ch)) {
result.append(ch);
} else if (ch == '(') {
stack.push(ch);
} else if (ch == ')') {
while (!stack.isEmpty() && stack.peek() != '(') {
result.append(stack.pop());
}
stack.pop(); // 弹出左括号
} else if (isOperator(ch)) {
while (!stack.isEmpty() && getPriority(stack.peek()) >= getPriority(ch)) {
result.append(stack.pop());
}
stack.push(ch);
}
}
// 弹出栈中剩余的操作符
while (!stack.isEmpty()) {
result.append(stack.pop());
}
return result.toString();
}
public static void main(String[] args) {
String expression = "a+b*(c^d-e)^(f+g*h)-i";
String postfix = infixToPostfix(expression);
System.out.println("后缀表达式为: " + postfix);
}
}
解决方式:
- 堆栈的使用: 操作符依次压入堆栈,遇到右括号或优先级较低的操作符时,进行
pop()操作。 - 时间复杂度: O(n),其中 n 是表达式的长度。
- 适用场景: 这种表达式求解方式可用于电商系统中的复杂规则计算,例如折扣规则计算、积分计算等。
5.5 矩阵旋转问题
问题描述: 给定一个 n x n 的矩阵,要求顺时针旋转 90 度。
示例: 输入:
csharp复制代码[
[1, 2, 3],
[4, 5, 6],
[7, 8, 9]
]
输出:
csharp复制代码[
[7, 4, 1],
[8, 5, 2],
[9, 6, 3]
]
解决方式: 该问题可以通过先转置矩阵,然后再翻转每一行来解决。虽然这个问题并不直接依赖堆栈,但通过借助堆栈的 LIFO 特性,也可以模拟旋转矩阵的过程。
public class RotateMatrix {
public static void rotate(int[][] matrix) {
int n = matrix.length;
// 1. 先转置矩阵
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
int temp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = temp;
}
}
// 2. 翻转每一行
for (int i = 0; i < n; i++) {
for (int j = 0; j < n / 2; j++) {
int temp = matrix[i][j];
matrix[i][j] = matrix[i][n - 1 - j];
matrix[i][n - 1 - j] = temp;
}
}
}
public static void main(String[] args) {
int[][] matrix = {
{1, 2, 3},
{4, 5, 6},
{7, 8, 9}
};
rotate(matrix);
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix[i].length; j++) {
System.out.print(matrix[i][j] + " ");
}
System.out.println();
}
}
}
解决方式:
- 步骤1 - 转置矩阵: 通过交换矩阵的行和列位置,将矩阵转置。对于
matrix[i][j]和matrix[j][i]进行交换操作,转置完成后矩阵的列变成了行。 - 步骤2 - 翻转每一行: 对于转置后的矩阵,每一行的元素从左到右翻转,这一步骤完成后,矩阵即为顺时针旋转 90 度的结果。
- 时间复杂度: O(n^2),其中 n 是矩阵的维度,因为每个元素都需要被访问一次。
- 适用场景: 这种矩阵旋转方法在图像处理、游戏开发等领域中非常常见,能够高效处理二维数据的旋转。
5.6 栈的最小元素问题
问题描述: 设计一个栈,支持常数时间复杂度的获取栈中最小元素操作。
示例: 操作:
push(1)push(2)push(-1)getMin()返回-1pop()getMin()返回1
解决方式:
要实现常数时间复杂度的获取栈中最小元素,我们可以使用两个栈:一个主栈和一个辅助栈。辅助栈始终保持当前主栈中的最小元素。
import java.util.Stack;
public class MinStack {
private Stack<Integer> stack;
private Stack<Integer> minStack;
public MinStack() {
stack = new Stack<>();
minStack = new Stack<>();
}
public void push(int x) {
stack.push(x);
if (minStack.isEmpty() || x <= minStack.peek()) {
minStack.push(x);
}
}
public void pop() {
int popped = stack.pop();
if (popped == minStack.peek()) {
minStack.pop();
}
}
public int top() {
return stack.peek();
}
public int getMin() {
return minStack.peek();
}
public static void main(String[] args) {
MinStack minStack = new MinStack();
minStack.push(1);
minStack.push(2);
minStack.push(-1);
System.out.println(minStack.getMin()); // 输出 -1
minStack.pop();
System.out.println(minStack.getMin()); // 输出 1
}
}
解决方式:
- 主栈: 存储所有入栈的元素。
- 辅助栈: 存储每个主栈状态下的最小元素。每次入栈时,如果当前元素小于等于辅助栈的栈顶元素,则将该元素也压入辅助栈;每次出栈时,如果出栈的元素等于辅助栈的栈顶元素,则辅助栈也出栈。
- 时间复杂度: O(1),无论是
push、pop还是getMin操作,时间复杂度均为常数时间。 - 适用场景: 这种设计在需要频繁访问最小元素并且要求高效的场景非常有用,例如实时监控数据的最小值。

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献8条内容
已为社区贡献8条内容





所有评论(0)