【计算机图形学】圆绘制算法-Bresenham
若d≤0,则先将d更新为d+2x+3,再将(x,y)更新为(x+1,y);否则先将d更新为d+2(x-y)+5,再将(x,y)更新为(x+1,y-1)。圆心在原点,半径为R的第一象限上的一段圆弧。且取(0,R)为起点,按顺时针方向绘制该1/8圆弧。3.绘制点(x,y)及其在八分圆中的另外七个对称点。2.计算初始值d=1.25-R、x=0、y=R。5.当x<=y时,重复步骤3和4。对于圆上的点,有F
原理分析与算法描述
-
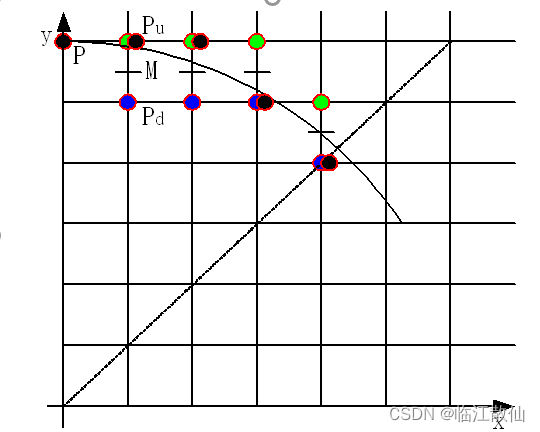
待绘制的圆弧
圆心在原点,半径为R的第一象限上的一段圆弧。且取(0,R)为起点,按顺时针方向绘制该1/8圆弧。
-
决策方程
F ( x , y ) = x 2 + y 2 − R 2 F(x,y)=x^2+y^2-R^2 F(x,y)=x2+y2−R2
对于圆上的点,有F(x,y)=0;对于圆外的点,F(x,y)>0;
对于圆内的点,F(x,y)<0。

M的坐标为: M ( x i + 1 , y i − 0.5 ) M(x_i+1,y_i-0.5) M(xi+1,yi−0.5)
•当 F ( x M , y M ) < 0 F(x_M,y_M)<0 F(xM,yM)<0时,取 P u ( x i + 1 , y i ) P_u(x_i+1,y_i) Pu(xi+1,yi)
•当 F ( x M , y M ) > 0 F(x_M,y_M)>0 F(xM,yM)>0时,取 P d ( x i + 1 , y i − 1 ) P_d(x_i+1,y_i-1) Pd(xi+1,yi−1)
•当 F ( x M , y M ) = 0 F(x_M,y_M)=0 F(xM,yM)=0时,约定取 P u P_u Pu。
-
构造判别式
d i = F ( x M , y M ) = F ( x i + 1 , y i − 0.5 ) = ( x i + 1 ) 2 + ( y i − 0.5 ) 2 − R 2 d_i=F(x_M,y_M)=F(x_i+1,y_i-0.5)=(x_i+1)^2+(y_i-0.5)^2-R^2 di=F(xM,yM)=F(xi+1,yi−0.5)=(xi+1)2+(yi−0.5)2−R2
•当 d i ≤ 0 d_i≤0 di≤0时,下一点取 P u ( x i + 1 , y i ) P_u(x_i+1,y_i) Pu(xi+1,yi);•当 d i > 0 d_i>0 di>0时,下一点取 P d ( x i + 1 , y i − 1 ) P_d(x_i+1,y_i-1) Pd(xi+1,yi−1)。
-
误差项的递推
d i < = 0 , d i + 1 = F ( x i + 2 , y i − 0.5 ) = d i + 2 x i + 3 d_i<=0,d_{i+1}=F(x_i+2,y_i-0.5)=d_i+2x_i+3 di<=0,di+1=F(xi+2,yi−0.5)=di+2xi+3;
d i > 0 , d i + 1 = F ( x i + 2 , y i − 1.5 ) = d i + 2 ( x i − y i ) + 5 d_i>0,d_{i+1}=F(x_i+2,y_i-1.5)=d_i+2(x_i-y_i)+5 di>0,di+1=F(xi+2,yi−1.5)=di+2(xi−yi)+5;
d 0 = F ( 1 , R − 0.5 ) = 1.25 − R d_0=F(1,R-0.5)=1.25-R d0=F(1,R−0.5)=1.25−R
-
算法步骤
1.输入圆的半径R。
2.计算初始值d=1.25-R、x=0、y=R。
3.绘制点(x,y)及其在八分圆中的另外七个对称点。
4.判断d的符号。若d≤0,则先将d更新为d+2x+3,再将(x,y)更新为(x+1,y);否则先将d更新为d+2(x-y)+5,再将(x,y)更新为(x+1,y-1)。
5.当x<=y时,重复步骤3和4。否则结束。
代码实现
std::vector<Point> DrawCircle(Point center, float radius)
{
std::vector<Point> points;
int x = 0, y = radius;
int d = 1.25 - radius;//决策变量初始值
int xc = center.x, yc = center.y;
while (y >= x) {//八对称点
points.push_back({ xc + x, yc + y });
points.push_back({ xc + x, yc - y });
points.push_back({ xc - x, yc + y });
points.push_back({ xc - x, yc - y });
points.push_back({ xc + y, yc + x });
points.push_back({ xc + y, yc - x });
points.push_back({ xc - y, yc + x });
points.push_back({ xc - y, yc - x });
if (d <= 0) {//更新决策变量和坐标
d = d + 2 * x + 3;
x += 1;
}
else {
d = d + 2 * (x - y) + 5;
x += 1, y -= 1;
}
}
return points;
}
结果展示

算法优化
- 改进:用d-0.25代替d,减少浮点数运算

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容





所有评论(0)