贝叶斯公式

参考：YouTobe

一、案例引入

$$P(A|B)=\frac{P(B|A)P(A)}{P(B)}$$

$$P(A\cap B)=P(A|B)\times P(B)=P(B|A)\times P(A)$$

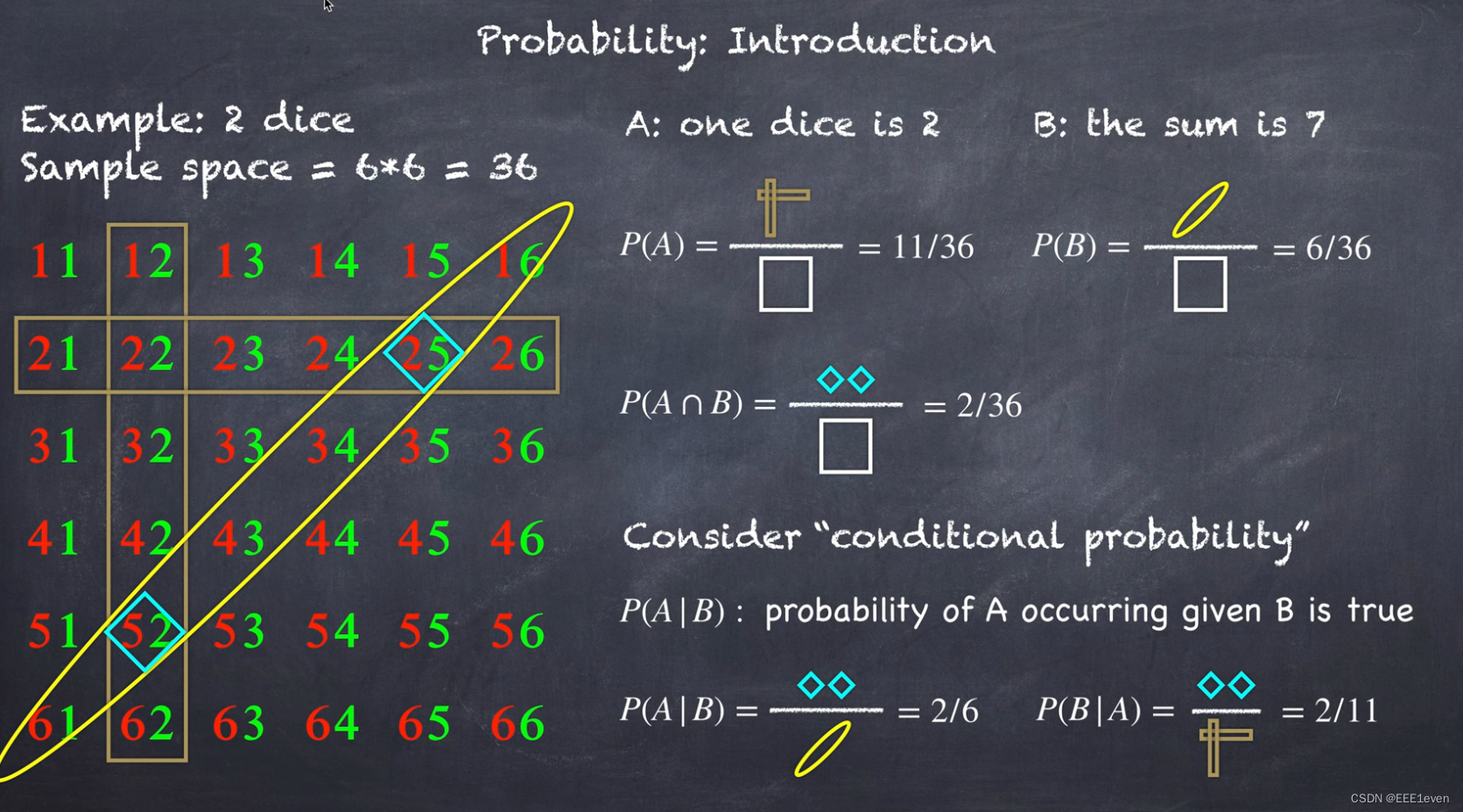
下图给出抛骰子的例子，解释如何推出贝叶斯公式

二、贝叶斯通式

$$P(H|E)=\frac{P(E|H)P(H)}{P(E)}E=Evidence,H=Hypothesis$$

贝叶斯定理关注的是：在已知的证据下，假设成立的概率有多大

三、公式推理

以上图为参考进行下述公式推理：

$$\bar{H}:notHP(\bar{H})=1-P(H)$$

$$P(E)=P(E\cap H)+P(E\cap \bar{H})=P(E|H)P(H)+P(E|\bar{H})P(\bar{H})$$

$$P(H|E)=\frac{P(E|H)P(H)}{P(E|H)P(H)+P(E|\bar{H})P(\bar{H})}$$

可以看到贝叶斯公式中分母为证据 $E$ 的概率，但是我们有时并不知道证据 $E$ 的概率，需要通过条件概率来计算 $P(E)$

四、举例理解

案例一

小明是一个内敛的人，他总是乐于助人，有一个温顺整洁的灵魂，他总是对自己有所要求，并规矩的生活，对细节非常在意。请问小明更可能是农民还是图书管理员？

Fact：图书管理员与农民的比例是1：50

	样本空间	符合条件	概率
图书管理员	10	5	9%
农民	500	50	91%

接下来用贝叶斯公式进行推导：

$E:statementbypeople$

$P(H):P(librarian)=\frac{1}{1+50}=0.0196$

$P(\bar{H}):P(farmer)=\frac{50}{1+50}=0.9804$

假设：$P(E|H)=0.5P(E|\bar{H})=0.1$

$$P(H|E)=\frac{P(E|H)P(H)}{P(E|H)P(H)+P(E|\bar{H})P(\bar{H})}$$

$P(H|E)=\frac{0.5\times 0.0196}{0.5\times 0.0196+0.1\times 0.9804}=0.0909$

所以得出：在证据 $E$ 成立（人们对小明的描述）的情况下， $H$ 事件（假设小明为图书管理员）发生的概率为 9.09%

案例二

你被检验出可能有一种罕见疾病

• 在人群中只有0.1%的人会得病

这个测试非常准确

• 如果有这个疾病，检查准确率达到99%
• 如果没有这个疾病，会有2%的误诊为患者

	1000人的样本空间	阳性	概率
疾病	1	1	$\frac{1}{20+1}$
健康	999	20	$\frac{20}{20+1}$

带入贝叶斯公式

$E$ : 你被检验出有罕见病

$P(H):患病概率=0.001$ （先验概率）

$P(\bar{H})=0.999$

$P(E|H):sensitivity=0.99$（真阳）

$P(E|\bar{H}):falsepositiverate=0.02$（假阳）

$$P(H|E)=\frac{P(E|H)P(H)}{P(E|H)P(H)+P(E|\bar{H})P(\bar{H})}$$

$P(H|E)=\frac{0.99\times 0.001}{0.99\times 0.001+0.02\times 0.999}=0.0472$（后验概率）

通过贝叶斯计算，你被检验出患有罕见病时，你真正患病的概率只有4.72%

如果再次检测还是为阳性

此时的相关证据与假设概率如下

$P(H)=0.0472$（后验概率：在第一次测得阳性的概率）

$P(\bar{H})=0.9528$

$P(E|H):sensitivity=0.99$（真阳）

$P(E|\bar{H}):falsepositiverate=0.02$（假阳）

除了假设患病概率以外，其他的不变

$$P(H|E)=\frac{P(E|H)P(H)}{P(E|H)P(H)+P(E|\bar{H})P(\bar{H})}$$

$P(H|E)=\frac{0.99\times 0.0472}{0.99\times 0.0472+0.02\times 0.9528}=0.7103$

可以看到，如果两次检测都为阳性，你患病的概率会一下子达到71.03%，与之前的4.72%形成了非常强的对比

上述的迭代运算也是贝叶斯的核心精神：通过不断的实验累积证据，从而更精准的判断一个假设是否正确

五、先验概率与后验概率

参考上述例子分析

先验概率是你提前已经知晓的概率（假设的实际概率）

而后验概率是在证据成立的前提下，确定假设成立的概率

通常情况下，后验概率我们是不得而知，需要通过贝叶斯公式来求得后验概率。所以贝叶斯也是一个求后验概率的公式

而更精准的判断一个假设是否正确

五、先验概率与后验概率

参考上述例子分析

先验概率是你提前已经知晓的概率（假设的实际概率）

而后验概率是在证据成立的前提下，确定假设成立的概率

通常情况下，后验概率我们是不得而知，需要通过贝叶斯公式来求得后验概率。所以贝叶斯也是一个求后验概率的公式