半导体物理基础-笔记
源内容参考:https://www.bilibili.com/video/BV11U4y1k7zn/?spm_id_from=333.337.search-card.all.click&vd_source=61654d4a6e8d7941436149dd99026962
源内容参考:https://www.bilibili.com/video/BV11U4y1k7zn/?spm_id_from=333.337.search-card.all.click&vd_source=61654d4a6e8d7941436149dd99026962
半导体物理要解决的四个问题
- 载流子在哪里;
- 如何获得足够多的载流子;
- 载流子如何运动;
- 哪些因素影响载流子的运动。
载流子可移动的条件
- 有电子或空穴;
- 有可被电子占据的空能态

能带论基本理论
- 对于半导体,当材料中的原子相互靠近形成分子时,能级会分裂成两个能带:导带和价带
- 在温度为0 K的时候,导带中全是空能态,价带中全是电子且价带中的能态被电子占满,在导带和价带中没有电子可能存在的能态,称为禁带(或带隙)

这种情况下,价带中没有空能态可供电子占据,因此电子在价带中不能移动。在导带中虽然有空能态,但是没有电子。因此,在温度为0 K时半导体材料中不存在可供导电的载流子。
薛定谔方程
i
ℏ
∂
ψ
∂
t
=
−
ℏ
2
2
m
∂
2
ψ
∂
r
2
+
V
ψ
i\hbar\frac{\partial \psi}{\partial t}=-\frac{\hbar^2}{2m}\frac{\partial^2\psi}{\partial r^2}+V\psi
iℏ∂t∂ψ=−2mℏ2∂r2∂2ψ+Vψ
从SE可以看出,势场的存在会对波产生作用,从而影响波的状态
自由粒子(散射态)
对于没有被任何势场影响的粒子,称为自由粒子。自由粒子的波矢的取值是连续的,相应的,其能量的取值也是连续的,这种状态称为“散射态”。
散射态
- 粒子的能量高于势垒,波函数可在整个空间存在
- 在远离势垒的位置,粒子存在的概率不等于零,波函数不可归一化
- 粒子的位置不被束缚
- 波矢k的取值是连续的,对应的能量E的取值也是连续的
束缚态
当粒子被束缚在某个势场中时,其能量低于势垒,因此在远离势垒的位置出现的概率为零,称为束缚态。
处于束缚态中的粒子的波矢k的取值是分立的,对应的能量E的取值也是分立的。
晶体中的势场与布洛赫电子
常用材料:Si、Ge、GaAs等
周期性势场
晶体中的原子具有周期性的排列结构,这种原子的周期性排列会形成周期性势场,其势场强度约为
1
0
8
V
/
cm
10^8~ V/\text{cm}
108 V/cm
布洛赫波函数
晶体中的电子的状态可用布洛赫波函数表达:
- k为波数
- u k ( x ) u_k(x) uk(x)是与晶格具有相同周期的周期性函数,即 u k ( x ) = u k ( x + n a ) u_k(x)=u_k(x+na) uk(x)=uk(x+na)
- 布洛赫波函数是平面波与周期函数的乘积
- 用布洛赫波函数描述的电子称为布洛赫电子
电子在周期性势场中的波函数可用布洛赫定理求解含周期性势场的薛定谔方程求得。
布洛赫电子的周期性边界条件

布里渊区
电子在周期性势场中运动的波函数,其振幅随位置周期性变化,且变化周期与晶格周期相同。因此晶格中的电子是以一个被调幅的平面波在晶体中传播,即周期性势场的作用是对平面波进行了调幅,并且由于周期性势场的微扰导致
E
(
k
)
E(k)
E(k)函数在
k
=
n
π
/
a
k=n\pi/a
k=nπ/a时断开,能量出现不连续,形成一系列允带(存在电子的能态,价带以及导带)。允带出现的区域称为“布里渊区”,每个布里渊区对应一个能带,禁带中不存在电子能态,其宽度取决于周期性势场的具体形式
轨道杂化
原子在形成分子的过程中,由于原子相互靠近,导致电子的波函数产生交叠,由此会发生“轨道杂化”。杂化后,轨道的数目不变,但其在空间的方向和分布以及能级会发生改变。
对于半导体材料,由于轨道杂化的作用,会使得其能级分裂成两个能带,即导带和价带。
禁带宽度
禁带中没有可供电子占据的能态,于是我们可通过给电子赋予能量的方式(加热或光照)使得价带中的电子跨过禁带跃迁到导带称为导电电子。要使得电子从价带跃迁到导带,就要给电子额外的能量,这个能量的最小值就是使价带顶的电子跃迁到导带底所需要的能量,称为禁带宽度。
不难看出,禁带宽度越宽的材料需要的能量越大。因此材料可根据导电性分为导体、半导体和绝缘体。
金属

- 要么导带中既有电子又有空能态;
- 要么导带和价带交叠在一起。
这种情况下电子根本不用额外能量越过禁带就有空能态可供占据,故金属是良好的导体。
绝缘体


对于绝缘体,其禁带宽度很宽,比如室温下半导体硅的禁带宽度为1.1 eV,而绝缘体金刚石的禁带宽度为5 eV。对于半导体,其禁带宽度小于绝缘体。
宽禁带半导体
一般将禁带宽度大于2.3 eV的半导体材料称为宽禁带半导体材料。主要有SiC、金刚石、II族氧化物、II族硫化合物、II族硒化合物、III族氮化合物以及这些材料的合金。(目前流行说第三代半导体本质上是禁带宽度更大的半导体,这些半导体材料禁带宽度大,热导率高,介电常数低,电子漂移饱和速度高等,适用于高频、高功率、高温、抗辐射以及高集成度器件。
禁带宽度随温度变化的规律
禁带宽度是随温度变化的,随着温度升高,禁带宽度按如下函数的形式减小:
E
g
(
T
)
=
E
g
(
0
)
−
α
T
2
T
+
β
E_g(T)=E_g(0)-\frac{\alpha T^2}{T+\beta}
Eg(T)=Eg(0)−T+βαT2
α
,
β
\alpha,\beta
α,β是相关的温度系数
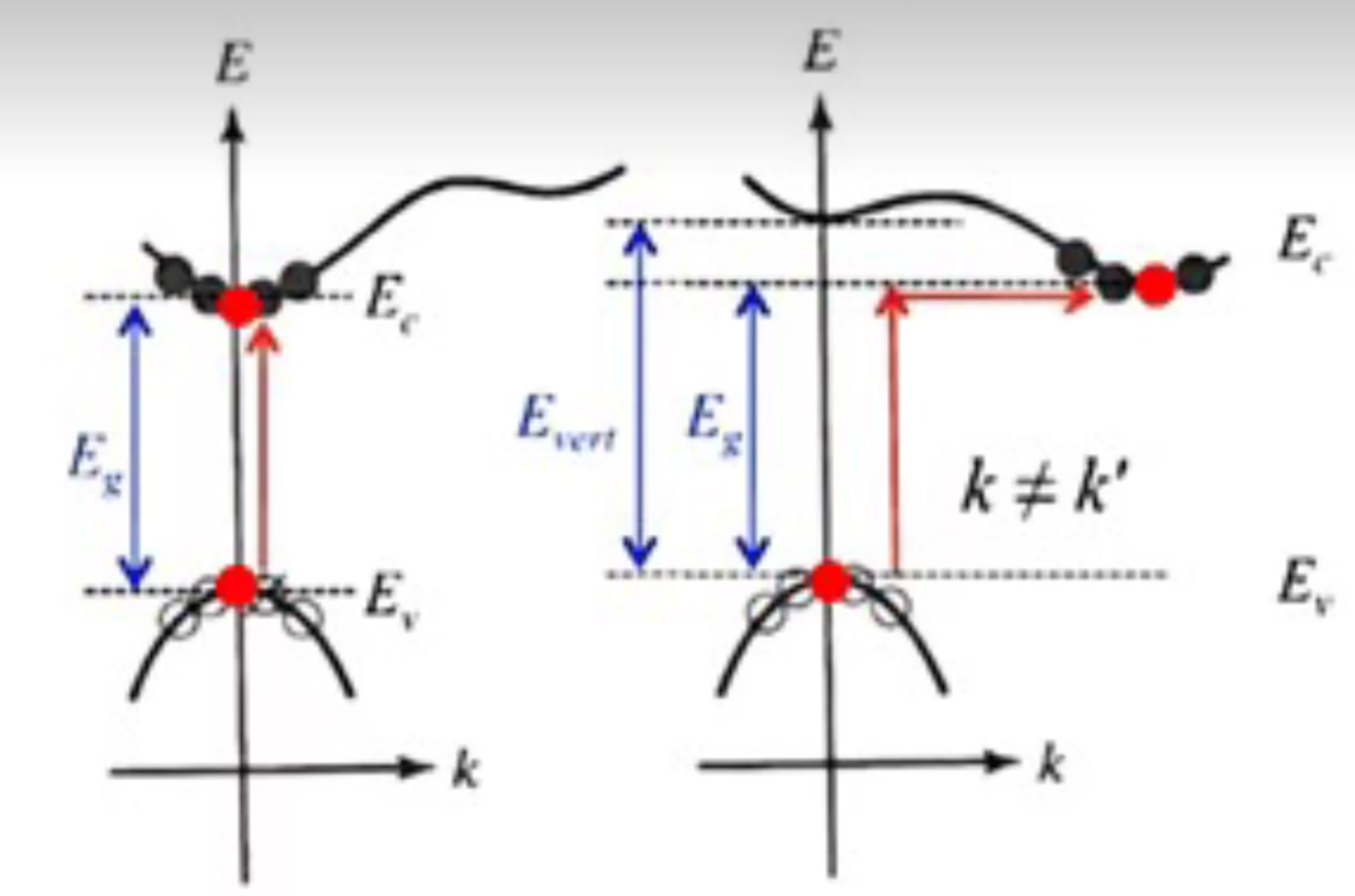
直接禁带半导体与间接禁带半导体
一些半导体的导带底不在波矢的原点(k=0)位置,因此电子的能量从价带顶跃迁到导带底会导致波矢发生改变(例如:硅),这种材料称为间接禁带半导体。而跃迁不伴随波矢改变的材料(例如:砷化镓)称为直接禁带半导体。
跃迁特性
- 直接禁带半导体:从导带底跃迁到价带顶时,能量以光子的形式释放,且光子的能量恰好等于禁带宽度;
- 间接禁带半导体:由于价带顶和导带底的k不同,在电子不改变动量和能量的情况下,是不能够从导带底直接跃迁到价带顶的, 因此通常需要通过禁带中的杂质,或者缺陷能级发生间接跃迁,间接跃迁过程中释放的能量一般以热能的形式传递给晶格,而不是发出光子。
所以,对于光电器件(例如:LED,LD等),要么选择直接禁带半导体作为材料。当选择间接禁带半导体作为材料的时候,需要使电子通过禁带中的缺陷或杂质能级发生垂直间接跃迁,这种情况下由于缺陷或杂质能级是位于禁带中,垂直间接跃迁时释放的能量小于禁带宽度,所以释放的光子的能量较低。
对于III~V族化合物半导体,当其组分发生变化时能带结构也会发生变化。既然有空能态的存在是载流子存在的必要条件,那么我们就必须研究一下材料中的能态分布情况。

能态密度

k空间

每一组
k
x
,
k
y
,
k
z
k_x,k_y,k_z
kx,ky,kz确定一个波矢
k
k
k,即确定一种准自由电子的运动状态。以这三个基矢张成的空间就是k空间。以k的各个取值画出平面,平面相交出来的每个六面体的顶点就表示每个粒子的态。六面体的体积就是每个态在k空间所占的体积。由于
k
x
,
k
y
,
k
z
k_x,k_y,k_z
kx,ky,kz的取值间隔相等,所以波矢密度在k空间分布是均匀的。
等能面
等能面是k空间具有相同能量的点构成的曲面。根据k空间与等能面的概念可知:
能态数目=波矢密度×等能面间体积
导带底附近和价带底附近的能态密度表达式
导带底附近的能态密度
g
c
(
E
)
=
4
π
V
(
2
m
n
∗
)
3
/
2
h
3
(
E
−
E
c
)
1
/
2
g_c(E)=4\pi V\frac{(2m^*_n)^{3/2}}{h^3}(E-E_c)^{1/2}
gc(E)=4πVh3(2mn∗)3/2(E−Ec)1/2
价带顶附近的能态密度
g
v
(
E
)
=
4
π
V
(
2
m
n
∗
)
3
/
2
h
3
(
E
v
−
E
)
1
/
2
g_v(E)=4\pi V\frac{(2m^*_n)^{3/2}}{h^3}(E_v-E)^{1/2}
gv(E)=4πVh3(2mn∗)3/2(Ev−E)1/2
其中
m
∗
m^*
m∗表示有效质量
费米-狄拉克统计分布
在热平衡条件下,从大量电子的整体来看,电子填充某一能量状态的概率服从费米-狄拉克统计分布:
f
(
E
)
=
1
e
(
E
−
E
F
)
/
k
B
T
+
1
f(E)=\frac{1}{e^{(E-E_F)/k_BT}+1}
f(E)=e(E−EF)/kBT+11
- f ( E ) f(E) f(E):费米-狄拉克分布函数,其指出了在热力学温度为T的热平衡条件下,系统内的某个允态E被电子占据的概率;
- E F E_F EF:费米能级,是基态(温度为0 K时的系统状态)时电子能填充的最高能级。费米能级与温度、固体材料的导电类型、杂质含量以及零点能的选取有关。只要知道了费米能级的取值,在一定温度下,电子在各能态的统计分布就可以完全确定;
- k B k_B kB:玻尔兹曼常数。
当温度高于0 K时,低于费米能级的各个能态被电子占据的概率大于1/2,等于费米能级的能态被占据的概率为1/2,高于费米能级的各能态被电子占据的概率小于1/2。因此费米能级在计算电子或空穴的浓度时起到标杆作用。
玻尔兹曼统计分布
当
(
E
−
E
F
)
>
>
k
B
T
(E-E_F)>>k_BT
(E−EF)>>kBT时,分母中的+1便可忽略,此时F-D分布函数可写为玻尔兹曼统计分布:
f
(
E
)
=
1
e
(
E
−
E
F
)
/
k
B
T
f(E)=\frac{1}{e^{(E-E_F)/k_BT}}
f(E)=e(E−EF)/kBT1
非简并半导体
半导体在大多数情况下,费米能级位于禁带中,且其到导带底或价带顶的距离远大于
k
B
T
k_BT
kBT,因此对半导体中最常研究的导带或价带中所有的量子态来说,电子或空穴都可以用玻尔兹曼统计分布描述,将能够用玻尔兹曼统计分布描述的半导体称为非简并半导体。
准经典粒子
通常情况下,晶体周期性势场的强度相当于
1
0
8
V
/
c
m
10^8 ~V/cm
108 V/cm,而外加场(电场、磁场、掺入晶体的杂质势场等),一般很难达到这种程度,因此外加场一般比周期势场弱得多。在这种情况下,可以认为在外加场的作用下,晶体的能带结构和电子的波函数基本不变,外加场的作用只是让电子能够从外场吸收能量,其能量的改变通过波矢k的改变来实现,但其状态的变化仍旧是在原来的能带结构的基础上,即电子不发生跃迁,运动只限于一个能带内。
在外场较弱,不考虑电子的干涉、衍射以及碰撞等情况下,可以把晶体中电子在外场中的运动当做准经典粒子来处理。当晶体存在外加场时,晶体中的电子除了受到内部周期性势场的作用以外,还受到外加场的作用。因此电子的加速度等于外加场和内部周期性势场综合作用的结果。
准经典粒子的有效质量

将内部势场的作用体现在有效质量中,而有效质量通常可以通过实验测定。由此,在计算电子受外场时的运动可以不必再涉及内场的作用,而直接引入有效质量进行计算,引入有效质量后,如果可以计算出有效质量的大小,便可确定能带极值附近的
E
(
k
)
E(k)
E(k)与
k
k
k的关系。有效质量既可为正也可为负,在能带底附近的电子有效质量总为正值,在能带顶附近的电子有效质量总是负值。一般情况下,电子的有效质量与空穴的有效质量并不相等。
为什么不能用本征半导体制作器件
虽然本征半导体通过热激发就可以产生载流子,但通常不能采用本征半导体来制作器件,这主要是因为:
- 纯度要求太高:要求本征载流子/总原子>杂质/总原子;
- 本征载流子浓度随温度变化很大,而载流子的浓度与电学性能强相关,对温度太敏感会造成器件性能的极不稳定。
掺杂半导体(doping,N/P)
当温度升高时,系统由基态变为激发态,电子受到热激发,室温下激发热能约为0.026 eV,远小于费米能(1.5 eV~15 eV),因此对于比费米能级低很多的电子是无法获得足够的能量来跳出费米能级的。这意味着即便是热激发,也只能使费米能级附近的小部分电子受到影响,而离费米能级较远的电子仍保持原来(0 K)时的状态。由此可见,对于本征半导体而言,在室温下由热激发而产生的载流子数量并不多,因此我们需要一种载流子浓度更高且可控、稳定性高的半导体材料——掺杂半导体。
通过在本征半导体中掺入杂质的方式,可以在半导体的禁带中引入杂质能级。杂质电离后,可以提供电子或空穴,从而改变半导体的导电性能。距离导带底或价带顶的能量差,便是杂质电离所需要的能量,其远小于禁带宽度。因此室温下一般掺入的杂质基本都电离了,这意味着我们需要载流子浓度是多少就掺杂等浓度的杂质即可。可在Si或者Ge中掺入V族元素,V族元素电离所需要的能量远小于禁带宽度。(V族元素杂质在Si或Ge中的电离能分别约为0.04~0.05 eV和0.01 eV;室温下Si和Ge的禁带宽度分别为1.12 eV和0.66 eV)。
N型半导体与施主杂质能级
V族元素电离后能够提供导电电子,从而增强导电能力,这种主要依靠电子导电的半导体称为N型半导体,掺入的V族元素称为施主杂质,其能级为施主杂质能级。

P型半导体与受主杂质能级
掺入III族元素电离后能够提供导电空穴,这种主要依靠空穴导电的半导体称为P型半导体,掺入的III族元素称为受主杂质,其能级为受主杂质能级。
载流子浓度分析计算(重难点)
对于非简并半导体:
- 导带中电子浓度 = 导带中电子的总数 / 体积
- 价带中电子浓度 = 价带中电子的总数 / 体积
导带中电子总数等于导带中能态数量乘以能态被电子占据的概率
在导带底附近,能量E到E+dE区间的能态数量为:
d
Z
(
E
)
=
g
c
(
E
)
d
E
\text{d}Z(E)=g_c(E)\text{d}E
dZ(E)=gc(E)dE
其中
g
c
(
E
)
g_c(E)
gc(E)为导带底附近(E到E+dE区间)的能态密度
电子占据能量为E的能态的概率为
f
(
E
)
f(E)
f(E),则在E到E+dE区间被电子占据的能态数量为:
f
(
E
)
g
c
(
E
)
d
E
f(E)g_c(E)\text{d}E
f(E)gc(E)dE
每个量子态上存在一个电子,因此在E到E+dE区间的电子数量为:
d
N
=
f
(
E
)
g
c
(
E
)
d
E
\text{d}N=f(E)g_c(E)\text{d}E
dN=f(E)gc(E)dE
将所有能量区间的电子数相加,即可得到能带中电子的总数,实际从导带底到导带顶的电子总数直接将
f
(
E
)
g
c
(
E
)
d
E
f(E)g_c(E)\text{d}E
f(E)gc(E)dE进行积分即可计算。再用电子的总数除以半导体体积即可计算出导带中电子浓度。
非简并半导体导带中电子浓度与价带中空穴浓度结论
非简并半导体导带中电子浓度
n
0
=
2
(
m
n
∗
k
0
T
2
π
ℏ
2
)
3
/
2
e
x
p
(
−
E
c
−
E
F
k
0
T
)
=
N
c
e
x
p
(
−
E
c
−
E
F
k
0
T
)
n_0=2(\frac{m^*_nk_0T}{2\pi\hbar^2})^{3/2}exp(-\frac{E_c-E_F}{k_0T})=N_cexp(-\frac{E_c-E_F}{k_0T})
n0=2(2πℏ2mn∗k0T)3/2exp(−k0TEc−EF)=Ncexp(−k0TEc−EF)
其中
m
n
∗
m^*_n
mn∗为电子有效质量,
k
0
k_0
k0为玻尔兹曼常数,
E
c
E_c
Ec为导带底能量,
E
F
E_F
EF为费米能级能量。
N
c
N_c
Nc为导带的有效能态密度:
N
c
=
2
(
m
n
∗
k
0
T
2
π
ℏ
2
)
3
/
2
N_c=2(\frac{m^*_nk_0T}{2\pi\hbar^2})^{3/2}
Nc=2(2πℏ2mn∗k0T)3/2,
N
c
∝
T
3
/
2
N_c\propto T^{3/2}
Nc∝T3/2。
非简并半导体价带中空穴浓度
p
0
=
2
(
m
p
∗
k
0
T
2
π
ℏ
2
)
3
/
2
e
x
p
(
−
E
F
−
E
v
k
0
T
)
=
N
v
e
x
p
(
−
E
F
−
E
v
k
0
T
)
p_0=2(\frac{m^*_pk_0T}{2\pi\hbar^2})^{3/2}exp(-\frac{E_F-E_v}{k_0T})=N_vexp(-\frac{E_F-E_v}{k_0T})
p0=2(2πℏ2mp∗k0T)3/2exp(−k0TEF−Ev)=Nvexp(−k0TEF−Ev)
其中
m
p
∗
m^*_p
mp∗为空穴有效质量,
N
v
N_v
Nv为价带的有效能态密度。
有效能态密度与温度和有效质量有关。
(非简并半导体)载流子浓度乘积结论
n
0
p
0
=
N
c
N
v
e
x
p
(
−
E
g
k
0
T
)
n_0p_0=N_cN_vexp(\frac{-E_g}{k_0T})
n0p0=NcNvexp(k0T−Eg)
其中
E
g
E_g
Eg为禁带宽度。
- 乘积与费米能级无关,即与所含杂质无关;
- 乘积中包含有效能态密度,因此浓度乘积与温度和有效质量有关;
- 乘积中包含禁带宽度,因此浓度乘积与材料本身有关。
综上可得,在一定的温度下,电子浓度与空穴浓度的乘积是一定的,即平衡状态下载流子浓度的乘积保持恒定。当电子浓度增大时,空穴浓度减小,反之亦然。该结论对于热平衡状态下的非简并半导体,无论是本征半导体还是杂质半导体均适用。
本征费米能级计算
对于本征半导体,在热平衡条件下,本征激发的电子和空穴是载流子的唯一来源。由于本征激发的电子和空穴是成对产生的,因此导带中电子浓度等于价带中空穴浓度:
n
0
=
p
0
=
n
i
n_0=p_0=n_i
n0=p0=ni,
n
0
p
0
=
n
i
2
n_0p_0=n_i^2
n0p0=ni2
其中
n
i
n_i
ni为本征载流子浓度。
可利用
n
0
=
p
0
=
n
i
n_0=p_0=n_i
n0=p0=ni来计算本征费米能级
E
F
i
E_{Fi}
EFi:
E
F
i
=
1
2
(
E
c
+
E
v
)
+
1
2
k
0
T
l
n
(
N
v
N
c
)
E_{Fi}=\frac{1}{2}(E_c+E_v)+\frac{1}{2}k_0Tln(\frac{N_v}{N_c})
EFi=21(Ec+Ev)+21k0Tln(NcNv)
代入
N
c
N_c
Nc和
N
v
N_v
Nv的方程得到:
E
F
i
=
1
2
(
E
c
+
E
v
)
+
3
4
k
0
T
l
n
(
m
p
∗
m
n
∗
)
E_{Fi}=\frac{1}{2}(E_c+E_v)+\frac{3}{4}k_0Tln(\frac{m^*_p}{m^*_n})
EFi=21(Ec+Ev)+43k0Tln(mn∗mp∗)
容易观察到,
1
2
(
E
c
+
E
v
)
\frac{1}{2}(E_c+E_v)
21(Ec+Ev)恰好是禁带
E
g
E_g
Eg的中央。
- 如果 m n ∗ = m p ∗ m^*_n=m^*_p mn∗=mp∗,则 l n ( m p ∗ m n ∗ ) = 0 ln(\frac{m^*_p}{m^*_n})=0 ln(mn∗mp∗)=0,即本征半导体费米能级 E F i E_{Fi} EFi严格位于禁带中央;
- 如果 m n ∗ < m p ∗ m^*_n<m^*_p mn∗<mp∗,则 l n ( m p ∗ m n ∗ ) ln(\frac{m^*_p}{m^*_n}) ln(mn∗mp∗)>0,即 E F i E_{Fi} EFi稍高于禁带中央;
- 如果 m n ∗ > m p ∗ m^*_n>m^*_p mn∗>mp∗,则 l n ( m p ∗ m n ∗ ) < 0 ln(\frac{m^*_p}{m^*_n})<0 ln(mn∗mp∗)<0,即 E F i E_{Fi} EFi稍低于禁带中央。
本征费米能级的位置与空穴和电子的有效质量之比有关。
载流子的热平衡
热平衡下,电子-空穴对的热产生率=复合率,即
g
i
=
r
i
g_i=r_i
gi=ri。
n
i
n_i
ni在更高的温度下达到新的平衡值。
即满足函数关系:
g
i
(
T
)
=
r
i
(
T
)
g_i(T)=r_i(T)
gi(T)=ri(T)
n
i
(
T
)
=
n
0
(
T
)
=
p
0
(
T
)
n_i(T)=n_0(T)=p_0(T)
ni(T)=n0(T)=p0(T)
当温度一定时,载流子的热产生率,即单位时间单位体积内热激发的电子-空穴对数目是固定的。但载流子浓度不随时间变化,这是因为在热激发下,虽然本征半导体在不断地产生电子-空穴对,但同时也存在与之相反的复合过程在不断发生,即导带的电子跃迁至价带并与价带中的空穴复合,以此消灭电子-空穴对。
当温度升高时,热产生率会增大,载流子浓度也增大,同时复合率也增大,这个过程的结果是对于更高的温度有更高的载流子浓度,即在更高的温度下达到新的平衡值。
总之,在热平衡状态下:
- 载流子的产生率等于复合率
- **费米能级的位置恒定不变(即在一个平衡半导体系统中,费米能级处处相等) **
- 载流子浓度由费米能级
E
F
E_F
EF决定(即费米能级越靠近导带,电子浓度越高于空穴浓度;费米能级越靠近价带,电子浓度越低于空穴浓度)
掺杂半导体载流子浓度
掺入施主杂质
对于掺杂半导体,电离了的施主杂质能给导带提供电子,没电离的施主杂质就仍然在施主能级上,那么施主能级上的电子浓度
n
D
n_D
nD就是没有电离的杂质的浓度。
假设掺入的施主杂质浓度为
N
D
N_D
ND,未电离的施主杂质浓度为
n
D
=
N
D
f
D
(
E
)
n_D=N_Df_D(E)
nD=NDfD(E),
因此电离了的杂质浓度等于:
n
D
+
=
N
D
−
n
D
n^+_D=N_D-n_D
nD+=ND−nD
其中
f
D
(
E
)
f_D(E)
fD(E)为电子占据施主能级的概率:
f
D
(
E
)
=
1
1
+
1
g
D
exp
(
E
D
−
E
F
k
0
T
)
f_D(E)=\frac{1}{1+\frac{1}{g_D}\text{exp}(\frac{E_D-E_F}{k_0T})}
fD(E)=1+gD1exp(k0TED−EF)1
掺入受主杂质
假设掺入的受主杂质浓度为
N
A
N_A
NA,未电离的受主杂质浓度为
p
A
=
N
A
f
A
(
E
)
p_A=N_Af_A(E)
pA=NAfA(E)
因此电离了的受主杂质浓度等于:
p
A
−
=
N
A
−
p
A
p^-_A=N_A-p_A
pA−=NA−pA
其中
f
A
(
E
)
f_A(E)
fA(E)为空穴占据受主能级的概率:
f
A
(
E
)
=
1
1
+
1
g
A
exp
(
E
F
−
E
A
k
0
T
)
f_A(E)=\frac{1}{1+\frac{1}{g_A}\text{exp}(\frac{E_F-E_A}{k_0T})}
fA(E)=1+gA1exp(k0TEF−EA)1
其中,
g
D
g_D
gD是施主能级的基态简并度,
g
A
g_A
gA是受主能级的基态简并度,称为简并因子。对于Si、Ge、GaAs等材料,
g
D
=
2
g_D=2
gD=2,
g
A
=
4
g_A=4
gA=4。
占据概率不同于F-D分布函数的原因
电子或者空穴占据施主或受主能级的概率与费米-狄拉克分布函数并不相同,这是因为对于施主能级而言,其要么只被一个电子占据,要么不被电子占据,绝对不可能同时被两个电子占据;对于受主能级,其要么被一个空穴占据,要么不被空穴占据,绝对不可能同时被两个空穴占据。
电中性条件
- 电中性条件: n 0 + p A − = p 0 + n D + n_0+p^-_A=p_0+n^+_D n0+pA−=p0+nD+
- N型半导体的电中性条件: n 0 = p 0 + n D + ( p A − = 0 ) n_0=p_0+n^+_D\;\;(p^-_A=0) n0=p0+nD+(pA−=0)
- P型半导体的电中性条件:
p
0
=
n
0
+
p
A
−
(
n
D
+
=
0
)
p_0=n_0+p^-_A\;\;(n^+_D=0)
p0=n0+pA−(nD+=0)
温度对掺杂半导体的载流子浓度的影响

半导体器件一般工作在饱和区,当温度区间位于饱和区时,杂质全部电离并且本征激发可忽略,此时:
- 对于N型半导体:导带中的电子浓度就是施主杂质浓度;
- 对于P型半导体:价带中的空穴浓度就是受主杂质浓度。
在本征激发仍可忽略的情况下,载流子浓度不会发生变化,因为没有更多杂质可供电离了。因此“室温下杂质全部电离”这句话本身忽略了杂质浓度的因素,杂质浓度越高,达到全部电离所需的温度越高,因此可通过适当控制(增加)掺杂浓度,从而使得器件在较大的温度范围内工作在对温度不敏感的饱和区。
掺杂半导体的费米能级与温度及杂质浓度的关系图

- 在温度一定的条件下,施主杂质浓度越高,费米能级越靠近导带底;受主杂质浓度越高,费米能级越靠近价带顶。
- 在浓度一定的条件下,温度越高,费米能级越靠近本征能级。
- 杂质浓度越高,费米能级达到本征能级所需的温度越高。

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献7条内容
已为社区贡献7条内容





所有评论(0)