自然语言处理(NLP)—— 主题建模
Dirichlet 分布是一个连续多变量概率分布,它是对多项分布中参数的先验分布。简单来说,如果你有一个多项分布(即一个分布,其中的事件有多个可能的类别,比如掷骰子的六个面),Dirichlet 分布可以用来表示这些类别分布的不确定性。Dirichlet 分布的参数是一组正实数,这些参数本身被称为"浓度参数"。分布的结果是一组满足以下条件的值每个都在 0 和 1 之间,即。所有的总和为 1,即。这
1. 主题建模的概念
主题建模(Topic Modeling)是一种用于发现文档集合(语料库)中的主题(或称为主题、议题、概念)的统计模型。在自然语言处理和文本挖掘领域,主题建模是理解和提取大量文本数据隐藏主题的一种常用方法。
1.1 主题建模的关键特点
主题:在主题建模中,主题通常被定义为一组共现的词汇,这些词汇在语料库中的文档集合里代表了某种特定的概念或话题。
词汇的概率:每个主题都由一组单词及其相关概率构成,这些概率表示了单词在该主题中的重要性或出现频率。
单词的多主题属性:同一个单词可以出现在多个主题中,并且在不同主题中具有不同的概率。这反映了词汇在不同语境下的多义性。
主题的解释性:生成的主题可能在语义上是有意义的,即它们代表了容易理解和识别的概念;也可能是抽象的,不容易直接解释。
1.2 主题建模的算法
隐含狄利克雷分布(Latent Dirichlet Allocation, LDA):LDA是最广泛使用的主题建模算法之一。它假设文档是由多个主题的混合生成的,每个主题又是由多个单词的混合生成的。
非负矩阵分解(Non-negative Matrix Factorization, NMF):NMF通过分解词频矩阵来发现文档-主题和主题-词汇之间的关系。
1.3 主题建模的应用
主题建模可以应用于许多场景,包括但不限于:
文档分类:通过识别文档的主要主题来对其进行分类。
推荐系统:通过发现用户兴趣的主题来提升内容推荐的相关性。
信息检索:增强搜索算法,让其能根据主题而非单个关键词来检索文档。
趋势分析:在时间序列数据中识别和跟踪主题的流行度变化。
通过主题建模,研究人员和数据分析师能够从大量的文本数据中抽象出有用的信息,以便进一步的分析和决策制定。
2. 潜在语义分析(Latent Semantic Analysis,LSA)
潜在语义分析(Latent Semantic Analysis,LSA)是一种用于文本处理的技术,可以揭示文档集合中隐藏的语义结构。LSA通过数学模型捕获词语与文档之间的关系,并能够减少数据的噪声和维度,从而发现词义上的模式和趋势。
2.1 LSA的关键步骤
2.1.1 构建术语/文档矩阵M
每一行代表一个文档,每一列代表一个术语(单词)。
2.1.2 使用TF-IDF代替术语计数
这里,
-
是单词
在文档
中的词频-逆文档频率值。
-
是单词
在文档
中出现的次数。
-
是文档总数,
是包含单词
的文档数。
2.1.3 执行奇异值分解(SVD)
奇异值分解是将矩阵M分解为三个矩阵的乘积:。
-
是一个包含非负递减实数的对角矩阵。
-
和
是半正交矩阵(即满足
或
的矩阵)。
LSA(潜在语义分析)是一种用于文本处理的技术,通过矩阵分解来识别文档集合中的潜在主题。在LSA中,主要涉及三个矩阵:U、S和。
U矩阵:它具有与文档数量相同的行数,其列由M的列聚合而来,这些列代表主题,因此U是一个文档-主题矩阵。
矩阵:它的列数与M中的术语数量相同,其行由M的行聚合而来,这些行代表与U中相同的主题,因此V是一个术语-主题矩阵。
决定主题数量N:在LSA中,我们需要决定主题的数量N,这是一个重要的参数,因为它影响模型的性能和主题的解释性。
2.1.4 获得最优的主题数量N
要获得最优的主题数量N,没有一个统一的标准答案,但可以通过以下方法来估计:
试错法:选择不同的N值,分别构建模型,然后评估每个模型的性能和主题的解释性。通常,可以使用诸如困惑度(Perplexity)之类的指标来评估模型的性能,低困惑度通常意味着模型性能好。
主题一致性:评估模型生成的主题的一致性或稳定性。主题一致性高的模型倾向于产生具有明确含义的、相互区分度高的主题。
人工评估:通过专业知识对生成的主题进行评估,选择能够最好地反映文档集合内容的主题数量。
2.1.5 降维
取的前N列,
的前N行和列,以及
的前N行来减少问题的维度。
这样做是为了保留数据中最重要的语义特征,同时去除那些对于主题不太重要或者是噪声的维度。
2.2 LSA的应用
发现文档和术语之间的隐含关系:LSA可以帮助识别文档中的主题或概念,并将术语与这些主题或概念关联起来。
改进信息检索:通过更好地理解文档内容的语义,LSA可以提高搜索引擎的准确性。
文本聚类和分类:LSA的降维特性可以用于文本聚类和分类任务,提高模型性能。
LSA虽然是一个较为古老的方法,但它仍然是文本挖掘和自然语言处理中一个非常有价值的工具。通过揭示文本数据中的隐含语义结构,LSA能够支持各种文本分析任务。
2.3 主题示例
主题示例展示了通过LSA技术从文档集合中提取的不同主题。每个主题都是由一系列术语组成,这些术语代表了主题的核心内容。例如,主题0可能与面试有关,而主题1可能与警察、事故和法庭相关。通过分析这些主题,我们可以对文档集合中的内容有更深入的了解,每个主题提供了文档集中某个特定方面的视角。
Topic 0:
interview extended michael john david smith james andrew mark scott
Topic 1:
police death probe crash woman fire call court missing drug
Topic 2:
say plan council call govt back fire australia water court
Topic 3:
say australia police minister need report must world could labor
Topic 4:
court face fire woman murder charged charge accused death crash
Topic 5:
call say medium australia inquiry change prompt spark opposition health
Topic 6:
fire house home govt crew australia sydney school blaze threat
Topic 7:
australia back world south australian take first test lead win
Topic 8:
council australia fire rate rise seek woman considers coast land
Topic 9:
back council claim fight fire hit say take push market选择最优主题数量的过程涉及到综合考量模型的解释性、性能指标以及实际应用需求。在实际操作中,可能需要多次尝试和评估,以找到最适合特定文档集合的主题数量。此外,通过观察和解释每个主题中最重要的术语,研究者可以更好地理解文档集合的潜在结构和含义。
每个主题下列出的术语反映了与该主题相关联的关键概念和实体,通过这些术语,可以快速把握每个主题的核心内容。例如,主题1聚焦于与法律、紧急情况和安全相关的事件,而主题7则可能关注于体育竞赛和国际竞赛成绩。
潜在语义分析不仅能帮助我们发现文本数据中的隐含主题,还可以用于文档分类、信息检索、文本相似性分析等多种应用场景,从而提高信息检索的准确性和文本分析的深度。
3. LDA
Latent Dirichlet Allocation (LDA) 是一种广泛应用于文本挖掘和主题建模的统计模型,它能够从大量的文档集合中发现隐含的主题结构。LDA 基于 Dirichlet 分布作为其核心数学原理之一,以此来模拟文档中主题的分布以及主题中词汇的分布。

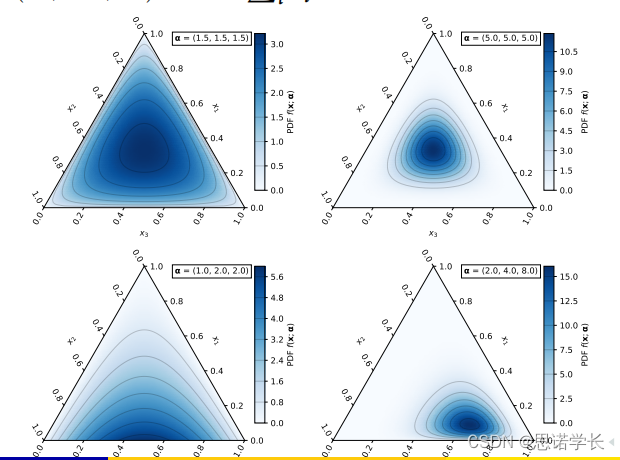
3.1 Dirichlet 分布简介
Dirichlet 分布是一个连续多变量概率分布,它是对多项分布中参数的先验分布。简单来说,如果你有一个多项分布(即一个分布,其中的事件有多个可能的类别,比如掷骰子的六个面),Dirichlet 分布可以用来表示这些类别分布的不确定性。
Dirichlet 分布的参数是一组正实数,这些参数本身被称为"浓度参数"。分布的结果是一组满足以下条件的值
:
每个 都在 0 和 1 之间,即
。
所有的总和为 1,即
。
这些性质使得 Dirichlet 分布非常适合表示一个文档中不同主题的比例,或者一个主题中不同词汇的比例,因为这两种情况都涉及到了一系列比例的表示,且这些比例的总和为 1。
3.2 LDA 中的应用
在 LDA 模型中,Dirichlet 分布被用作两个层次的先验分布:
文档-主题分布:每个文档都被假设为由多个主题组成,其比例遵循 Dirichlet 分布。参数反映了主题分布的先验知识,比如我们假设文档中各个主题的分布是均匀的,还是有某些特定主题更可能出现。
主题-词汇分布:同样地,每个主题被假设为由多个词汇组成,其比例也遵循 Dirichlet 分布。参数(通常与
不同)反映了词汇分布的先验知识。
通过这种方式,LDA 能够自动从文档集合中学习到隐含的主题,并且能够表达出每个文档中这些主题的比例以及每个主题中不同词汇的比例,这对于文本分析和理解具有重要价值。
3.3 LDA潜在狄利克雷分配的图形模型

3.3.1 图形参数的解释
这张图是一个Latent Dirichlet Allocation(LDA,潜在狄利克雷分配)的图形模型,用来展示如何从文档中抽取主题和它们的分布。在这个模型中:
α(Alpha):这是一个参数,影响文档中主题分布的形状。一个较大的α值可能意味着每个文档包含的主题更均匀分布,而较小的α值意味着文档更可能倾向于一小部分主题。α是大小为K的向量,其中K是主题的数量,我们对M个文档进行这样的处理。
θ(Theta):表示一个特定文档中不同主题的分布,它是从Dirichlet(α)分布中抽样得到的。
Z:这是主题分配变量,表示给定文档中的每个词被分配到的主题。
W:这是观察到的单词变量,代表文档中的实际单词。
β(Beta):这是一个参数,影响主题中词汇分布的形状。和α参数类似,一个较大的β值表示每个主题中词汇分布更均匀,而较小的β值表示某些词汇在主题中的权重更重。β是大小为V的向量,V是词汇表的大小,我们对K个主题进行这样的处理。
ϕ(Phi):表示一个特定主题中不同词汇的分布,它是从Dirichlet(β)分布中抽样得到的。
在这个模型中,每个文档都通过其θ向量有一个主题分布,θ向量是从α参数的Dirichlet分布中采样得到的。同样,每个主题都通过其ϕ向量有一个词汇分布,ϕ向量是从β参数的Dirichlet分布中采样得到的。这种结构允许每个文档表现出多个主题,每个主题也包含多个词汇。通过这种方式,LDA可以发现隐藏在大量文本数据背后的主题结构,这对于文本挖掘和信息检索非常有用。
3.3.2 在LDA模型中的处理步骤
LDA(潜在狄利克雷分配)是一种主题模型,它允许我们对文档集合中的文档和词汇进行主题分配。对于给定的文档,在LDA模型中的处理步骤如下:
a.为每个词汇选择主题:对于文档中的每个词汇(文档中共有N个词汇),我们从多项分布Polynomial(θ)中抽取一个样本主题。这里的θ是这个文档的主题分布,它表示不同主题在该文档中的比例。
b.确定词汇属于主题的概率:对于每个词汇,我们也有一个概率φ(phi),它表示该词汇属于给定主题的概率。φ是由该主题的词汇分布决定的,这个分布说明了每个词汇属于该主题的可能性。
c.计算主题与文档的关联概率:我们可以计算文档中每个词汇属于不同主题的概率。这是通过θ和φ的乘积得到的,因为θ给出了文档属于各个主题的概率,而φ给出了每个主题中各个词汇的概率。
d. 利用这些概率在算法中:通过结合文档的主题概率θ和词汇的主题概率φ,我们可以估计文档中每个词汇属于各个主题的概率。这些概率可以用来推断文档的主题结构,以及主题本身的词汇构成。
e. 迭代优化:LDA通常使用迭代算法(如吉布斯抽样或变分贝叶斯方法)来优化θ和φ,使得模型能够最好地解释观测到的词汇分布。这些迭代算法通过调整θ和φ的估计来最大化数据的似然性或某些后验概率。
在多次迭代之后,我们得到了稳定的主题分布θ和词汇分布φ,这样就能对每个文档的主题构成以及每个主题中词汇的重要性有了较好的估计。这允许我们对文档进行分类、理解其内容、以及探究不同主题之间的关系。
3.3.3 LDA算法
LDA(潜在狄利克雷分配)算法是一个用于发现文本集合中潜在主题的过程。以下是其步骤的中文解释:
a. 随机分配主题:在所有文档中,我们随机给每个词汇分配一个主题。
b. 准备表格:建立两个表格,一个记录每个文档中各个主题的出现次数,另一个记录每个词分配给主题的情况。
c. 循环所有词汇:对所有文档中的每个词汇开始循环。假设我们现在处理的是文档中的词汇
,这个词汇当前分配到主题
。现在,我们把这个词汇从它当前的主题中去除,并在第1步建立的两个表格中各减去一个单位。
d. 计算概率并更新分配:然后,我们计算这个词汇属于每个主题的概率,并重新为它分配一个最有可能的主题。具体计算如下:
是文档
中分配给主题
的词汇比例,计算公式为
,其中
是文档
中分配到主题
的词的数量,
是文档
的总词数,
是平滑超参数。
是主题
生成词汇
的概率,计算公式为
,其中
是词汇
分配给主题
的次数,
是词汇表的大小,
是另一个平滑超参数。
e. 主题重新分配:我们选择使 最大的
作为词汇
的新主题,并更新表格。
f. 重复步骤2到4:对所有文档中的每个词汇重复以上步骤。
g. 多次迭代:重复步骤1到5指定的迭代次数,直到算法稳定,通常这个过程会逐步提高整个模型的准确性。
通过这个迭代过程,LDA算法能够发现文档集合中的主题,并估算文档中词汇分布以及词汇与主题之间的关联。这个模型非常有用,可以帮助我们理解和组织大量的文本数据。
4. 总结LSA(潜在语义分析)与LDA(潜在狄利克雷分配)
LSA(潜在语义分析)与LDA(潜在狄利克雷分配)都是用于从文本数据中抽取主题的技术,但它们在数学原理和应用效果上有所不同。
LSA的主题是通过奇异值分解(SVD)从术语-文档矩阵中提取的。这种方法基于线性代数,能够减少数据的维度,挖掘词和文档之间的关系。
LDA的主题是通过迭代计算每个文档的主题分布和每个主题的词分布来得到的。这个过程基于统计推断,特别是贝叶斯推断,能够更好地处理文本数据的多义性和噪声。
以下是两种方法各自提取的主题内容:
LSA的主题示例:
主题0:与个人采访有关的关键词。
主题1:涉及警察、死亡、事故调查等安全问题。
主题2:关于政府规划、议会活动及政府决策。
主题3:包括有关澳大利亚、警察、政府官员的话题。
主题4:与法庭、火灾、谋杀案和其他重大事件有关。
...(依此类推,总结每个主题的核心内容)
LDA(100次迭代后)的主题示例:
主题0:涉及事故报告、市场、失踪案件等。
主题1:与政府政策、水资源管理、农业相关的话题。
主题2:包括警察、女性、学校、国家事务等内容。
主题3:围绕医院、健康、政府选举、胜利等议题。
主题4:变化、农村事务、谈话、价格上涨等话题。
...(依此类推,总结每个主题的核心内容)
在实际应用中,LDA通常被认为比LSA更先进,因为它考虑到了词的多义性和文本数据中的不确定性。LDA的主题通常也更加一致和清晰。然而,这两种技术都能提供有价值的见解,选择哪种方法取决于具体的应用场景和需求。
5. 主题一致性的评估方法
评估主题的一致性是主题模型质量评估的关键环节。它用于衡量一个主题中的词是否经常共同出现,这样的主题通常对人类来说更加连贯、更易理解。Newman等人(2010年)和Mimno等人(2011年)提出的UCI一致性和UMass一致性就是这样的评估指标。
5.1 UCI一致性
UCI一致性使用了PMI(逐点互信息)作为计算的基础。
PMI是一种统计量,用于衡量两个词\(w_i\)和\(w_j\)共同出现的频率是否高于随机共同出现的频率。
通过在维基百科等大型语料库上使用滑动窗口来计算共现概率,PMI的计算公式为:
其中,是两个词共现的概率,
和
分别是两个词独立出现的概率,
是一个小的正数,用于避免对数运算中的除零错误。
UCI一致性是通过对一个主题中所有可能的词对计算PMI并求和得到的。
5.2 UMass一致性
UMass一致性与UCI类似,但它是一个不对称的量度,只考虑特定顺序的词对。
UMass一致性的计算方法为:
其中,是两个词共现的概率,
是第一个词出现的概率。
5.3 一致性结果CUCI
负的PMI值意味着词的组合趋势比随机组合更低。
根据您提供的数据,LSA的一致性分数是−1.439,LDA经过1次迭代后是−2.140,10次迭代后是−1.957,100次迭代后是−1.921。
这些数值表示LDA模型随着迭代次数的增加一致性有所提高,也就是说模型的质量在逐渐变好,词更倾向于与其他相关词共同出现。
在使用这些指标时,较高(较不负)的一致性分数通常表明模型的主题更加连贯,与人类的判断更为一致。在实际应用中,选择最佳的主题模型往往需要综合这些指标与其他因素,如主题的解释性和应用的特定需求。

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献14条内容
已为社区贡献14条内容





所有评论(0)