数据插值

在图像处理领域，图像的放缩、去畸变、旋转会用到插值；在机器学习、深度学习等领域，面对样本较少的情况时同样会用到插值。当我们进行数据分析时，遇到数据量小、样本点不足的情况，这时就需要利用插值。从定义的角度出发，在给定离散点的基础上，通过插值算法得到一条经过所有n个离散点的曲线，根据曲线信息以及插值点信息来获取插值点的坐标，而插值的作用在于根据现有数据样本点增加样本数据量，其本质是获取新的数据点坐标信息。

数据拟合

根据测试数据建立数学模型，是工程中最为常见的拟合问题。数据拟合的意义在于：可实现针对测试数据的精确或最佳逼近、量化总体趋势并支持预测分析，通过拟合模型可以滤除噪声数据，同时支持数据点估值以及极值或最值寻优。

在MWORKS.Syslab中，数据插值的使用步骤为：数据插值预处理→创建插值模型函数→提取插值数据→图形可视化。具体操作如下：

◎  数据插值预处理

首先准备原始数据，生成9个数据以及内插xt1和外插xte的点位。

xs = 1:9
ys = [19.21 , 18.15 , 15.36 , 18.10 , 16.89 , 11.32 , 7.45 , 5.24 , 7.01]

xt1 = 1:0.01:9 #插值点
xte = 0:0.01:10 #外插点

◎  创建插值模型函数

根据已有数据和选取方法创建插值模型函数。在Syslab中利用interpolate等函数和已知样本数据，创建插值模型函数，其代码如下所示：

# 最邻近样条插值
itp1_Ntp = ConstantInterpolation(xs,ys)
# 线性样条插值
itp1_linear = LinearInterpolation(xs,ys)
# 调用interpolate插值函数并设置插值模式inerpmode
itp1_spl2 = interpolate(ys,BSpline(Quadratic(Natural(OnGrid())))) 
# 调用CubicSplineInterpolation样条插值函数并设置插值类型为外插
itp1_spl3 = CubicSplineInterpolation(xs,ys,extrapolation_bc=Line())

对于更高的插值度数（特别是二次样条插值及以上），样条插值无法计算出数据集边缘附近的值，并且需要求解方程组以获得插值系数，为此必须指定用于闭合系统的边界条件，即Flat、Line、Natual、Free、Periodic和Reflect。在指定边界条件时必须明确其适用对象，即作用在边界网格(OnGrid())还是应用在下一个（虚构的）网格点 (OnCell()) 中间的边缘点。

边界条件
Flat()	将外推斜率设置为零。
Line()	使用恒定斜率进行外推。
Periodic()	应用于周期性边界条件。
Reflect()	应用于反射边界条件。
Quadratic (bc::BoundaryCondition)	表示对应的轴应该使用二次插值。
边界条件适用对象
OnGrid()	表示边界条件适用于第一个和最后一个节点。
OnCell()	表示边界条件在第一个和最后一个节点之外应用半网格间距。

（表1 边界条件与边界条件适用对象）

所有上述概念各自在类型层次结构中都有一个表示，从根本上影响插值函数的行为。

◎  提取插值数据

利用创建插值模型函数作用于目标点的x轴坐标，获取目标点的坐标点信息，提取数据。

y_Ntp = itp1_Ntp(xt1)# 获取最邻近插值数据点
y_linear = itp1_linear(xt1)# 获取线性样条插值数据点
y_spl2 = itp1_spl2(xt1) # 获取二次样条插值数据点
y_spl3 = itp1_spl3(xte) # 获取三次样条插值数据点

◎  图形可视化

最后绘制结果图像，其代码如下：​​​​​​​

#绘制插值结果图
figure("样条插值")
grid("on")
hold("on")
p1 = plot(xt1, y_Ntp, "k-") # 最邻近插值
p2 = plot(xt1, y_linear, "r") # 线性插值
p3 = plot(xt1, y_spl2, "b") # 二次插值
p4 = plot(xte, y_spl3, "#00FF00") # 三次样条 S(3,2)
p0 = plot(xs, ys, "o", markersize = 10, markeredgecolor = "b", markerfacecolor = "#FFFF00")
legend(["最邻近样条插值", "线性样条插值", "二次样条插值", "三次样条插值(外插)", "原始数据"], fontsize = 10)
xlabel("Xdata", fontsize = 10)
ylabel("Value", fontsize = 10)
title("一维样条插值", fontsize = 10)
hold("off")

插值方法的实现是根据原有数据进行插值后得到插值函数，输入自变量得到对应插值结果。Syslab为用户提供多项式插值、最邻近插值、线性插值、B样条插值、散点插值等多种方法。

MWORKS.Syslab插值方法
LinearInterpolation	线性插值
CubicSplineInterpolation	三次样条插值
Sinc_interpolate	一维插值（FFT方法）
ConstantInterpolation	最邻近插值
NewtonInterp	牛顿插值
LagrangeInterp	拉格朗日插值
interpolate	可根据参数调整算法的插值函数
Extrapolate	可根据参数调整算法的外插函数

在MWORKS.Syslab中，数据拟合的基本步骤为：数据预处理→模型定义→数据拟合→结果分析→图形可视化。以曲线拟合为例：

◎ 数据预处理

对数据异常点进行清洗、消除，得到如下散点图：

◎ 模型定义

定义目标曲线模型。

fitting(a,b,x) = a*b*x^(b-1)*exp(-a*x^b)

◎  数据拟合

调用WeibullFit函数对数据进行韦布尔拟合，得到目标模型的关键参数a,b。​​​​​​​

# 韦布尔拟合
a,b = WeibullFit(xdata,ydata)

◎  结果分析

在曲线拟合中，计算误差平方和SSE，判断数据拟合效果。​​​​​​​

# 计算误差平方和
SSE1 = SSE(ydata,fitting.(a,b,xdata))

◎  图形可视化

    1.设置绘图点​​​​​​​

xplot = LinRange(0.1,6,100)
yplot = fitting.(a,b,xplot) # 获取拟合数据点以便绘图

    2.拟合结果绘图

a = @sprintf("%0.4f",a)
b = @sprintf("%0.4f",b)
SSE1 = @sprintf("%0.4f",SSE1)
figure("Weibull拟合")
hold("on")
plot(xdata,ydata,"o",markersize = 8,markerfacecolor = "#FFFF00",markeredgecolor = "k")
title("Weibull拟合\n SSE:$SSE1  a = $a b = $b",fontsize = 10)
xlabel("xdata",fontsize = 10)
ylabel("value",fontsize = 10)
plot(xplot,yplot,"r")
legend(["原始数据","拟合曲线 y = a*b*x^(b-1)*exp(-a*x^b)"],fontsize = 10)
grid("on")

此外，Syslab还提供了二维拟合的算法和函数，示例如下：

◎ 数据预处理

对数据异常点进行清洗、消除，得到如下散点图：

◎  模型定义

根据模型关键参数，定义目标模型。

fitting(x,y,a,b,c,d) = a*sin(x+b) + c*cos(y+d)

◎  数据拟合

可选择自定义函数，使用自定义方法LM算法进行曲面拟合，得到模型的关键参数。​​​​​​​

@variables x y z a b c d
func = a*sin(x+b) + c*cos(y+d) # 自定义目标函数
vars = getvariables2(func) # 获取变量
p = LM2(func,X,Y,Z,[1,2,1,3]) # 调用LM2算法获取参数
a,b,c,d = p # 参数赋值

◎ 结果分析

计算曲面拟合误差平方和SSE，结果为142.6952954371209。​​​​​​​

# 计算误差平方和
SSE1 = SSE(xdata,fitting.(xdata,ydata,a,b,c,d))

◎  图形可视化

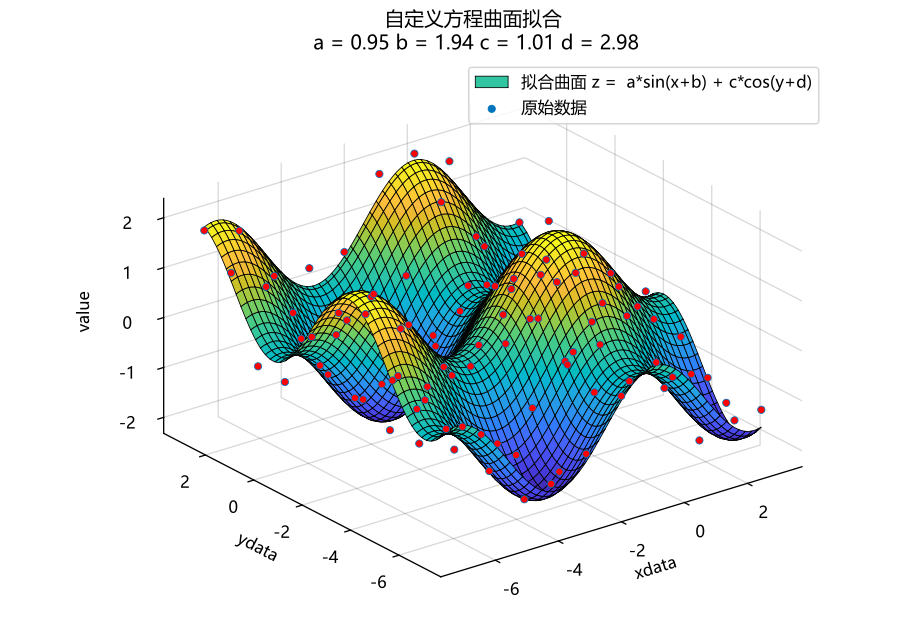
拟合结果绘图。

a = @sprintf("%0.2f",a)
b = @sprintf("%0.2f",b)
c = @sprintf("%0.2f",c)
d = @sprintf("%0.2f",d)
figure("自定义方程曲面拟合")
surf(Xplot,Yplot,Zplot)
hold("on")
scatter3(X,Y,Z,filled = true,facecolors = "r",s = 20)
title("自定义方程曲面拟合\n a = $a b = $b c = $c d = $d")
xlabel("xdata")
ylabel("ydata")
zlabel("value")
legend(["拟合曲面 z =  a*sin(x+b) + c*cos(y+d)" , "原始数据"])
hold("off")

数据拟合的实现是对数据集x,y进行指数拟合，从而获得固定表达式形式的曲线或自定义方程的关键参数。Syslab针对曲线拟合提供了线性拟合、指数拟合、对数拟合、幂拟合、多项式拟合、正弦拟合、韦布尔拟合、以及自定义方程曲线拟合。针对曲面拟合提供了二元多项式拟合以及自定义方程曲面拟合。

MWORKS.Syslab数据拟合
LinearFit	线性拟合：得到的直线数学表达式为
ExpFit	指数拟合：获得的拟合曲线为
LogFit	对数拟合：获得的拟合曲线为
PowerFit	幂拟合：获得的拟合曲线为  或
PolyFit	多项式拟合：获得的拟合曲线为
RationalFit	有理分式拟合：获得的拟合曲线为
SumofSineFit	正弦拟合：获得的拟合曲线如下，其中正弦函数个数为n
WeibollFit	韦布尔拟合：获得的拟合曲线为
LM	自定义方程曲线拟合
LM2	自定义方程曲面拟合

本文利用Syslab的基础数学库实现了对工程中几类典型的基于数据的插值与拟合，详细插值与拟合函数用法可参见Syslab基础数学库帮助文档。

MWORKS.Syslab作为新一代高级科学计算环境，可以高效解决科学与工程中遇到的矩阵运算、数值求解、数据分析、信号处理、控制算法设计优化、机器学习与并行计算等问题，实现基于模型对现代信息物理融合系统（CPS）开发的全流程支撑。

同元软控为用户提供免费版本的MWORKS.Syslab，欢迎大家前往同元软控官网自行下载。

下载地址：www.tongyuan.cc/download

点击查看原文：Syslab使用攻略 | 数据插值与数据拟合Syslab基础数学库实现了工程中基于数据的插值与拟合https://mp.weixin.qq.com/s/KPhPqGrl3x5WjFzsXy4rUg