文章参考

• https://www.cnblogs.com/kanjian2016/p/7746005.html
• https://blog.csdn.net/asialee_bird/article/details/81118245

ID3决策树

1、测试数据集

天气	温度	湿度	风速	活动
晴	炎热	高	弱	取消
晴	炎热	高	强	取消
阴	炎热	高	弱	进行
雨	适中	高	弱	进行
雨	寒冷	正常	弱	进行
雨	寒冷	正常	强	取消
阴	寒冷	正常	强	进行
晴	适中	高	弱	取消
晴	寒冷	正常	弱	进行
雨	适中	正常	弱	进行
晴	适中	正常	强	进行
阴	适中	高	强	进行
阴	炎热	正常	弱	进行
雨	适中	高	强	取消

代码创建如下：

'''
创建测试数据集
'''
def createDataset():
    dataSet = [['sunny', 'hot', 'high', 'weak', 'no'],
               ['sunny', 'hot', 'high', 'strong', 'no'],
               ['overcast', 'hot', 'high', 'weak', 'yes'],
               ['rain', 'mild', 'high', 'weak', 'yes'],
               ['rain', 'cool', 'normal', 'weak', 'yes'],
               ['rain', 'cool', 'normal', 'strong', 'no'],
               ['overcast', 'cool', 'normal', 'strong', 'yes'],
               ['sunny', 'mild', 'high', 'weak', 'no'],
               ['sunny', 'cool', 'normal', 'weak', 'yes'],
               ['rain', 'mild', 'normal', 'weak', 'yes'],
               ['sunny', 'mild', 'normal', 'strong', 'yes'],
               ['overcast', 'mild', 'high', 'strong', 'yes'],
               ['overcast', 'hot', 'normal', 'weak', 'yes'],
               ['rain', 'mild', 'high', 'strong', 'no']]  # 数据集
    labels = ['outlook', 'temperature', 'humidity', 'wind']  # 分类属性
    return dataSet, labels

代码创建的表与上述表格一一对应！

2、信息熵

通常熵表示事物的混乱程度，熵越大表示混乱程度越大，越小表示混乱程度越小。

假定当前样本集合 𝐷 共包含 ℓ 类样本, 其中第 𝑘 类样本所占的比例为 𝑝𝑘 (𝑘 = 1, 2, · · · , ℓ), 则 𝐷 的信息熵定义为：

以活动是否进行为例，在活动这一栏属性中，活动的取值有两种：取消(5个)和进行(9个)，则可以通过计算得到H(活动)，即活动的信息熵：

代码运算如下：

'''
计算香农熵
'''
def shannonEnt(dataSet):
    len_dataSet = len(dataSet)  # 得到数据集的行数
    labelCounts = {}  # 创建一个字典，用于计算，每个属性值出现的次数
    shannonEnt = 0.0  # 令香农熵初始值为0

    for element in dataSet:  # 对每一条数据进行逐条分析
        currentLabel = element[-1]  # 提取属性值信息
        if currentLabel not in labelCounts.keys():  # 以属性名作为labelCounts这个字典的key
            labelCounts[currentLabel] = 0  # 设定字典的初始value为0
        labelCounts[currentLabel] += 1  # value值逐渐加一，达到统计标签出现次数的作用

    for key in labelCounts:  # 遍历字典的key
        proportion = float(labelCounts[key])/len_dataSet
        shannonEnt -= proportion*log(proportion, 2)  # 根据公式得到香农熵

    print('属性值出现的次数结果：{}'.format(labelCounts))
    print('活动的信息熵为：{}'.format(shannonEnt))

    return shannonEnt

3、信息增益

假定离散属性 𝑎 有 𝑚 个可能的取值 {𝑎1, 𝑎2, · · · , 𝑎𝑚}, 若使用 𝑎 来对 样本集 𝐷 进行划分, 则会产生 𝑚 个分支结点, 其中第 𝑖 个分支结点包含 了 𝐷 中所有在属性 𝑎 上取值为 𝑎𝑖 的样本, 记为 𝐷𝑖. 可根据公式计算 出 𝐷𝑖 的信息熵, 再考虑到不同的分支结点所包含的样本数不同, 给分支 结点赋予权重 |𝐷𝑖|/|𝐷|, 即样本数越多的分支结点的影响越大, 于是可计算出用属性 𝑎 对样本集 𝐷 进行划分所获得的“信息增益。

其实也就是信息熵减去条件熵。
以求天气属性的信息增益为例
天气属性共有三种取值：晴（5个）、阴（4个）、雨（5个）

• 天气为晴时
  活动的取值有两种：取消（3个）和进行（2个）
  计算天气为晴时的条件熵：
  
• 天气为阴时
  活动的取值有一种：进行（4个）
  计算天气为阴时的条件熵：
  
• 天气为雨时
  活动的取值有两种：取消（2个）和进行（3个）
  计算天气为晴时的条件熵：
  

由此可以计算天气属性不同取值划分时的带权平均熵：

那么信息增益Gain(活动,天气)为：

同理，可以计算出Gain(活动,温度)、Gain(活动,湿度)、Gain(活动,风速)，通过比较大小，得到最大信息增益，并选择最大信息增益对应的属性作为决策树的根节点。

代码计算如下：

'''
划分数据集，从而更方便地计算条件熵
dataSet:数据集
i:划分数据集的属性（如：天气）的索引（0）
value:需要返回的属性的值（如：晴天）
'''


def splitDataSet(dataSet, i, value):
    splitDataSet = []  # 创建一个列表，用于存放 划分后的数据集
    for example in dataSet:  # 遍历给定的数据集
        if example[i] == value:
            splitExample = example[:i]
            splitExample.extend(example[i+1:])
            splitDataSet.append(splitExample)  # 去掉i属性这一列，生成新的数据集，即划分的数据集
    return splitDataSet  # 得到划分的数据集

'''
计算信息增益,从而选取最优属性（标签）
'''


def chooseBestFeature(dataSet):

    numFeature = len(dataSet[0]) - 1  # 求属性的个数
    baseEntropy = shannonEnt(dataSet)  # 测试数据集的香农熵，即信息熵
    bestInfoGain = 0.0  # 创建初始的最大信息增益，用于得到最终的最大信息增益
    bestFeature = -1  # 用于得到最大信息增益对应的属性 在数据集中的索引；其中-1，可以为任意数字（数字范围：小于0或大于等于numFeature）
    for i in range(numFeature):
        featList = [example[i] for example in dataSet]  # 得到第i个属性，对应的全部属性值
        featValue = set(featList)  # 创建一个set集合(集合中的元素不可重复),更容易看出全部属性值
        newEntropy = 0.0  # 创建初始条件熵，初始值为0
        for value in featValue:  # 对每一个属性值进行遍历
            subDataSet = splitDataSet(dataSet, i, value)  # 调用函数，进行数据集划分
            proportion = float(len(subDataSet)/len(dataSet))
            newEntropy += proportion*shannonEnt(subDataSet)  # 通过公式计算条件熵
        infoGain = baseEntropy - newEntropy  # 通过公式计算信息增益
        print('属性%s的信息增益为%.3f' % (labels[i], infoGain))  # 打印每个属性对应的信息增益

        if infoGain > bestInfoGain:   # 通过比较，选出最大的信息增益及其对应属性在数据集中的索引
            bestInfoGain = infoGain
            bestFeature = i

    print('最大增益对应的属性为：%s' % labels[bestFeature])

    return bestFeature

函数的图解

4、决策树的构建

ID3决策树算法：

• (1) 如果 𝐷 中所有实例属于同一类 𝐶𝑘, 则 𝑇 为单结点树, 并将类 𝐶𝑘 作为该结点的类标记, 返回 𝑇 .
• (2) 如果 𝐴 = ∅, 则 𝑇 为单结点树, 并将 𝐷 中类别数目最多的类 𝐶𝑘 作为该结点的类标记, 返回 𝑇 . 否则, 利用公式计算 𝐴 中每个属性对 𝐷 的信息增益, 选择信息增益最大的属性 𝐴𝑔.
• (3) 如果 𝐴𝑔 的信息增益小于阈值 𝜀, 则 𝑇 为单结点树, 并将 𝐷 中类别数目最多的类 𝐶𝑘 作为该结点的类标记, 返回 𝑇 . 否则, 对 𝐴𝑔 的每一种可 能值 𝑎𝑖, 依 𝐴𝑔 = 𝑎𝑖 将 𝐷 分割为若干非空子集 𝐷𝑖, 将 𝐷𝑖 中类别数目最多 的类作为标记, 构建子结点, 由结点及其子树构成树 𝑇 , 返回 𝑇 .
• 对第 𝑖 个子结点, 以 𝐷𝑖 为训练集, 以 𝐴∖{𝐴𝑔} 为属性集合, 递归调 用 (1)∼(3), 得到子树 𝑇𝑖, 返回 𝑇𝑖.

'''
统计classList中出现最多的类标签
'''
def maxLabel(classList):
    classCount = {}
    for vote in classList:  # 统计classCount中元素出现的次数
        if vote not in classCount.keys():
            classCount[vote] = 0
        classCount += 1
    # 根据字典的值降序排序，得到的结果是一个列表，列表中的元素是元组
    sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
    return sortedClassCount[0][0]  # 返回classCount中出现次数最多的元素

'''
构建决策树
'''
def creatTree(dataSet, labels, featLabels):
    classList = [example[-1] for example in dataSet]  # 获取分类标签（yes或no）
    if classList.count(classList[0]) == len(classList):  # 如果分类标签相同，则停止划分
        return classList[0]
    if len(dataSet[0]) == 1:  # 如果遍历完所有的属性，则返回结果中出现次数最多的分类标签
        return maxLabel(classList)
    bestFeature = chooseBestFeature(dataSet)  # 得到最大信息增益对应的属性在数据集中的索引
    bestFeatureLabel = labels[bestFeature]  # 得到最大信息增益对应的属性（如：天气）

    featLabels.append(bestFeatureLabel)

    myTree = {bestFeatureLabel: {}}  # 根据最大信息增益的标签生成树
    del(labels[bestFeature])  # 删除已经使用的属性
    featureList = [example[bestFeature] for example in dataSet]  # 得到数据集中最优属性的属性值（如：晴天，下雨）
    featureValue = set(featureList)  # 创建集合，去除重复的属性值
    for value in featureValue:
        subLabels = labels[:]  # 新的属性标签集合（与labels相比，去掉了已经使用的属性标签）
        # 递归调用creatTree，从而创建决策树
        myTree[bestFeatureLabel][value] = creatTree(splitDataSet(dataSet, bestFeature, value), subLabels, featLabels)
    # print(featLabels)
    return myTree

5、使用决策树进行决策

'''
使用决策树进行分类
'''
def classify(myTree, featLabels, testData):
    # global classLabel
    firstStr = next(iter(myTree))  # 得到决策树根节点
    # print(firstStr)
    secondDict = myTree[firstStr]  # 下一个字典
    # print(secondDict)
    featIndex = featLabels.index(firstStr)  # 得到根节点属性在测试数据集中对应的索引
    # print(featIndex)
    for key in secondDict.keys():
        if testData[featIndex] == key:
            if type(secondDict[key]).__name__ == 'dict':  # type().__name__的作用是，判断数据类型
                classLabel = classify(secondDict[key], featLabels, testData)
            else:
                classLabel = secondDict[key]
    return classLabel

6、决策树源码

# -*- coding: UTF-8 -*-
"""
# @Time: 2022/6/18 16:19
# @Author: 爱打瞌睡的CV君
# @CSDN: https://blog.csdn.net/qq_44921056
"""
from math import log
import operator
'''
创建测试数据集
'''
def createDataset():
    dataSet = [['sunny', 'hot', 'high', 'weak', 'no'],
               ['sunny', 'hot', 'high', 'strong', 'no'],
               ['overcast', 'hot', 'high', 'weak', 'yes'],
               ['rain', 'mild', 'high', 'weak', 'yes'],
               ['rain', 'cool', 'normal', 'weak', 'yes'],
               ['rain', 'cool', 'normal', 'strong', 'no'],
               ['overcast', 'cool', 'normal', 'strong', 'yes'],
               ['sunny', 'mild', 'high', 'weak', 'no'],
               ['sunny', 'cool', 'normal', 'weak', 'yes'],
               ['rain', 'mild', 'normal', 'weak', 'yes'],
               ['sunny', 'mild', 'normal', 'strong', 'yes'],
               ['overcast', 'mild', 'high', 'strong', 'yes'],
               ['overcast', 'hot', 'normal', 'weak', 'yes'],
               ['rain', 'mild', 'high', 'strong', 'no']]  # 数据集
    labels = ['outlook', 'temperature', 'humidity', 'wind']  # 分类属性
    return dataSet, labels

'''
计算香农熵
'''
def shannonEnt(dataSet):
    len_dataSet = len(dataSet)  # 得到数据集的行数
    labelCounts = {}  # 创建一个字典，用于计算，每个属性值出现的次数
    shannonEnt = 0.0  # 令香农熵初始值为0

    for element in dataSet:  # 对每一条数据进行逐条分析
        currentLabel = element[-1]  # 提取属性值信息
        if currentLabel not in labelCounts.keys():  # 以属性名作为labelCounts这个字典的key
            labelCounts[currentLabel] = 0  # 设定字典的初始value为0
        labelCounts[currentLabel] += 1  # value值逐渐加一，达到统计标签出现次数的作用

    for key in labelCounts:  # 遍历字典的key
        proportion = float(labelCounts[key])/len_dataSet
        shannonEnt -= proportion*log(proportion, 2)  # 根据公式得到香农熵

    # print('属性值出现的次数结果：{}'.format(labelCounts))
    # print('活动的信息熵为：{}'.format(shannonEnt))

    return shannonEnt
'''
划分数据集，从而更方便地计算条件熵
dataSet:数据集
i:划分数据集的属性（如：天气）的索引（0）
value:需要返回的属性的值（如：晴天）
'''


def splitDataSet(dataSet, i, value):
    splitDataSet = []  # 创建一个列表，用于存放 划分后的数据集
    for example in dataSet:  # 遍历给定的数据集
        if example[i] == value:
            splitExample = example[:i]
            splitExample.extend(example[i+1:])
            splitDataSet.append(splitExample)  # 去掉i属性这一列，生成新的数据集，即划分的数据集
    return splitDataSet  # 得到划分的数据集

'''
计算信息增益,从而选取最优属性（标签）
'''


def chooseBestFeature(dataSet):

    numFeature = len(dataSet[0]) - 1  # 求属性的个数
    baseEntropy = shannonEnt(dataSet)  # 测试数据集的香农熵，即信息熵
    bestInfoGain = 0.0  # 创建初始的最大信息增益，用于得到最终的最大信息增益
    bestFeature = -1  # 用于得到最大信息增益对应的属性 在数据集中的索引；其中-1，可以为任意数字（数字范围：小于0或大于等于numFeature）
    for i in range(numFeature):
        featList = [example[i] for example in dataSet]  # 得到第i个属性，对应的全部属性值
        featValue = set(featList)  # 创建一个set集合(集合中的元素不可重复),更容易看出全部属性值
        newEntropy = 0.0  # 创建初始条件熵，初始值为0
        for value in featValue:  # 对每一个属性值进行遍历
            subDataSet = splitDataSet(dataSet, i, value)  # 调用函数，进行数据集划分
            proportion = float(len(subDataSet)/len(dataSet))
            newEntropy += proportion*shannonEnt(subDataSet)  # 通过公式计算条件熵
        infoGain = baseEntropy - newEntropy  # 通过公式计算信息增益
        # print('属性%s的信息增益为%.3f' % (labels[i], infoGain))  # 打印每个属性对应的信息增益

        if infoGain > bestInfoGain:   # 通过比较，选出最大的信息增益及其对应属性在数据集中的索引
            bestInfoGain = infoGain
            bestFeature = i

    # print('最大增益对应的属性为：%s' % labels[bestFeature])

    return bestFeature

'''
统计classList中出现最多的类标签
'''
def maxLabel(classList):
    classCount = {}
    for vote in classList:  # 统计classCount中元素出现的次数
        if vote not in classCount.keys():
            classCount[vote] = 0
        classCount += 1
    # 根据字典的值降序排序，得到的结果是一个列表，列表中的元素是元组
    sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
    return sortedClassCount[0][0]  # 返回classCount中出现次数最多的元素

'''
构建决策树
'''
def creatTree(dataSet, labels, featLabels):
    classList = [example[-1] for example in dataSet]  # 获取分类标签（yes或no）
    if classList.count(classList[0]) == len(classList):  # 如果分类标签相同，则停止划分
        return classList[0]
    if len(dataSet[0]) == 1:  # 如果遍历完所有的属性，则返回结果中出现次数最多的分类标签
        return maxLabel(classList)
    bestFeature = chooseBestFeature(dataSet)  # 得到最大信息增益对应的属性在数据集中的索引
    bestFeatureLabel = labels[bestFeature]  # 得到最大信息增益对应的属性（如：天气）

    featLabels.append(bestFeatureLabel)

    myTree = {bestFeatureLabel: {}}  # 根据最大信息增益的标签生成树
    del(labels[bestFeature])  # 删除已经使用的属性
    featureList = [example[bestFeature] for example in dataSet]  # 得到数据集中最优属性的属性值（如：晴天，下雨）
    featureValue = set(featureList)  # 创建集合，去除重复的属性值
    for value in featureValue:
        subLabels = labels[:]  # 新的属性标签集合（与labels相比，去掉了已经使用的属性标签）
        # 递归调用creatTree，从而创建决策树
        myTree[bestFeatureLabel][value] = creatTree(splitDataSet(dataSet, bestFeature, value), subLabels, featLabels)
    # print(featLabels)
    return myTree


'''
使用决策树进行分类
'''
def classify(myTree, featLabels, testData):
    firstStr = next(iter(myTree))  # 得到决策树根节点
    # print(firstStr)
    secondDict = myTree[firstStr]  # 下一个字典
    # print(secondDict)
    featIndex = featLabels.index(firstStr)  # 得到根节点属性在测试数据集中对应的索引
    # print(featIndex)
    for key in secondDict.keys():
        if testData[featIndex] == key:
            if type(secondDict[key]).__name__ == 'dict':  # type().__name__的作用是，判断数据类型
                classLabel = classify(secondDict[key], featLabels, testData)
            else:
                classLabel = secondDict[key]
    return classLabel


if __name__ == '__main__':
    dataSet, labels = createDataset()  # 创建测试数据集及其标签
    featLabels = []  # 用于存放最佳属性值
    myTree = creatTree(dataSet, labels, featLabels)  # 生成决策树
    # print('决策树为:{}'.format(myTree))
    testData = ['sunny', 'hot', 'high', 'weak']  # 测试数据
    result = classify(myTree, featLabels, testData)  # 进行测试
    print('决策结果：{}'.format(result))

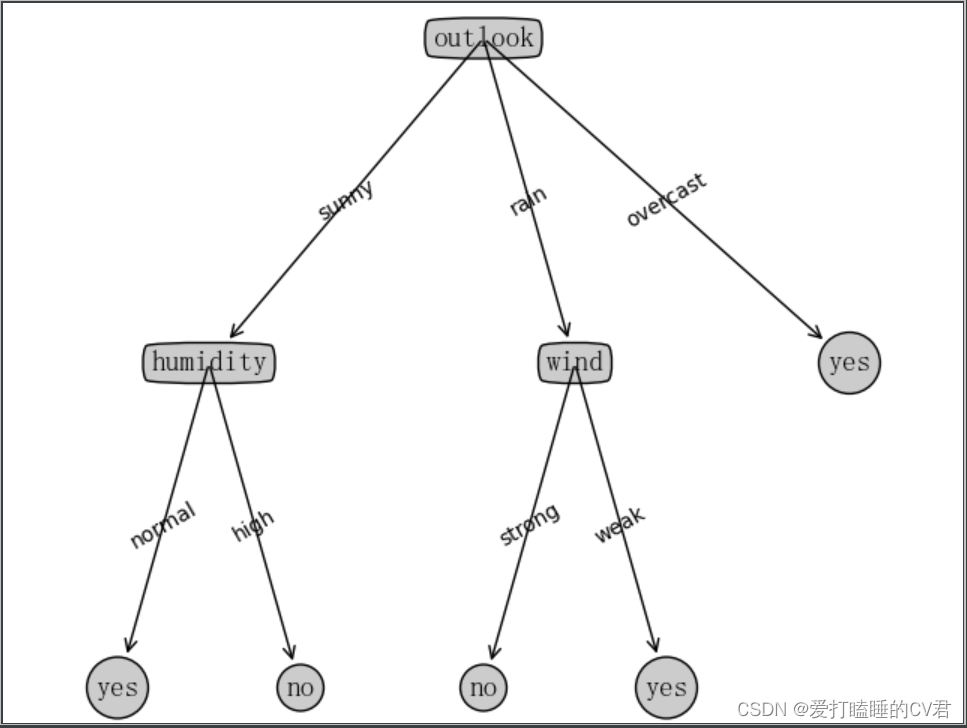
7、决策树可视化

其中demo是上部分编写决策树源码的文件名
绘图所用函数可参考：https://matplotlib.org/stable/tutorials/text/annotations.html#sphx-glr-tutorials-text-annotations-py

# -*- coding: UTF-8 -*-
"""
# @Time: 2022/6/19 16:44
# @Author: 爱打瞌睡的CV君
# @CSDN: https://blog.csdn.net/qq_44921056
"""
from matplotlib.font_manager import FontProperties
import matplotlib.pyplot as plt
import demo

# 定义文本框和箭头格式
decisionNode = dict(boxstyle='round4', fc='0.8')
leafNode = dict(boxstyle='circle', fc='0.8')
arrow_args = dict(arrowstyle='<-')
# 设置中文字体
font = FontProperties(fname=r"C:\Windows\Fonts\simsun.ttc", size=14)

"""
函数说明:获取决策树叶子结点的数目
Parameters:
    myTree - 决策树
Returns:
    numLeafs - 决策树的叶子结点的数目
"""


def getNumLeafs(myTree):
    numLeafs = 0  # 初始化叶子
    # python3中myTree.keys()返回的是dict_keys,不在是list,所以不能使用myTree.keys()[0]的方法获取结点属性，
    # 可以使用list(myTree.keys())[0]
    firstStr = next(iter(myTree))
    secondDict = myTree[firstStr]  # 获取下一组字典
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':  # 测试该结点是否为字典，如果不是字典，代表此结点为叶子结点
            numLeafs += getNumLeafs(secondDict[key])
        else:
            numLeafs += 1
    return numLeafs


"""
函数说明:获取决策树的层数
Parameters:
    myTree - 决策树
Returns:
    maxDepth - 决策树的层数
"""


def getTreeDepth(myTree):
    maxDepth = 0  # 初始化决策树深度
    # python3中myTree.keys()返回的是dict_keys,不在是list,所以不能使用myTree.keys()[0]的方法获取结点属性，
    # 可以使用list(myTree.keys())[0]
    firstStr = next(iter(myTree))
    secondDict = myTree[firstStr]  # 获取下一个字典
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':  # 测试该结点是否为字典，如果不是字典，代表此结点为叶子结点
            thisDepth = 1 + getTreeDepth(secondDict[key])
        else:
            thisDepth = 1
        if thisDepth > maxDepth:
            maxDepth = thisDepth  # 更新层数
    # print(maxDepth)
    return maxDepth


"""
函数说明:绘制结点
Parameters:
    nodeTxt - 结点名
    centerPt - 文本位置
    parentPt - 标注的箭头位置
    nodeType - 结点格式
"""


def plotNode(nodeTxt, centerPt, parentPt, nodeType):
    arrow_args = dict(arrowstyle="<-")  # 定义箭头格式
    font = FontProperties(fname=r"C:\Windows\Fonts\simsun.ttc", size=14)  # 设置中文字体
    createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',  # 绘制结点
                            xytext=centerPt, textcoords='axes fraction',
                            va="center", ha="center", bbox=nodeType, arrowprops=arrow_args, fontproperties=font)


"""
函数说明:标注有向边属性值
Parameters:
    cntrPt、parentPt - 用于计算标注位置
    txtString - 标注的内容
"""


def plotMidText(cntrPt, parentPt, txtString):
    xMid = (parentPt[0] - cntrPt[0]) / 2.0 + cntrPt[0]  # 计算标注位置
    yMid = (parentPt[1] - cntrPt[1]) / 2.0 + cntrPt[1]
    createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)


"""
函数说明:绘制决策树
Parameters:
    myTree - 决策树(字典)
    parentPt - 标注的内容
    nodeTxt - 结点名
"""


def plotTree(myTree, parentPt, nodeTxt):
    decisionNode = dict(boxstyle="round4", fc="0.8")  # 设置结点格式
    leafNode = dict(boxstyle="circle", fc="0.8")  # 设置叶结点格式
    numLeafs = getNumLeafs(myTree)  # 获取决策树叶结点数目，决定了树的宽度
    depth = getTreeDepth(myTree)  # 获取决策树层数
    firstStr = next(iter(myTree))  # 下个字典
    cntrPt = (plotTree.xOff + (1.0 + float(numLeafs)) / 2.0 / plotTree.totalW, plotTree.yOff)  # 中心位置
    plotMidText(cntrPt, parentPt, nodeTxt)  # 标注有向边属性值
    plotNode(firstStr, cntrPt, parentPt, decisionNode)  # 绘制结点
    secondDict = myTree[firstStr]  # 下一个字典，也就是继续绘制子结点
    plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD  # y偏移
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':  # 测试该结点是否为字典，如果不是字典，代表此结点为叶子结点
            plotTree(secondDict[key], cntrPt, str(key))  # 不是叶结点，递归调用继续绘制
        else:  # 如果是叶结点，绘制叶结点，并标注有向边属性值
            plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalW
            plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
            plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
    plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD


"""
函数说明:创建绘制面板
Parameters:
    inTree - 决策树(字典)
"""


def createPlot(inTree):
    fig = plt.figure(1, facecolor='white')  # 创建fig
    fig.clf()  # 清空fig
    axprops = dict(xticks=[], yticks=[])
    createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)  # 去掉x、y轴
    plotTree.totalW = float(getNumLeafs(inTree))  # 获取决策树叶结点数目
    plotTree.totalD = float(getTreeDepth(inTree))  # 获取决策树层数
    plotTree.xOff = -0.5 / plotTree.totalW
    plotTree.yOff = 1.0 # x偏移
    plotTree(inTree, (0.5, 1.0), '')  # 绘制决策树
    plt.show()


if __name__ == '__main__':
    dataSet, labels = demo.createDataset()
    featLabels = []
    myTree = demo.creatTree(dataSet, labels, featLabels)
    createPlot(myTree)

未来可期

文章到这里就要结束了，但故事还没有结局

如果本文对你有帮助，记得点个赞👍哟，也是对作者最大的鼓励🙇‍♂️。

如有不足之处可以在评论区👇多多指正，我会在看到的第一时间进行修正

作者：爱打瞌睡的CV君
CSDN：https://blog.csdn.net/qq_44921056
本文仅用于交流学习，未经作者允许，禁止转载，更勿做其他用途，违者必究。