环境：

• .net 6.0
• NetTopologySuite 2.5.0
• vs2022
• 平面二维

一、点与点关系

平面中两个点的关系最为简单,无非就是重合与否。
不过，需要注意的一点是：计算时可能需要考虑到容许的误差，比如，两个点相距小于0.0001 即认为重合。

直接看下面代码示例：

//平面内尽量使用 Equals2D(...)
var flag = new Coordinate(1, 1).Equals(new Coordinate(1, 1));//true
var flag2 = new Coordinate(1, 1).Equals2D(new Coordinate(1, 1));//true
var flag3 = new Coordinate(1, 1) == new Coordinate(1, 1);//false

//tolerance: 即为容忍的误差范围
var flag4 = new Coordinate(1, 1).Equals2D(new Coordinate(1, 1.0000056), tolerance: 0.0001);//true
var flag5 = new Coordinate(1, 1).Equals2D(new Coordinate(1, 1.01), tolerance: 0.0001);//false

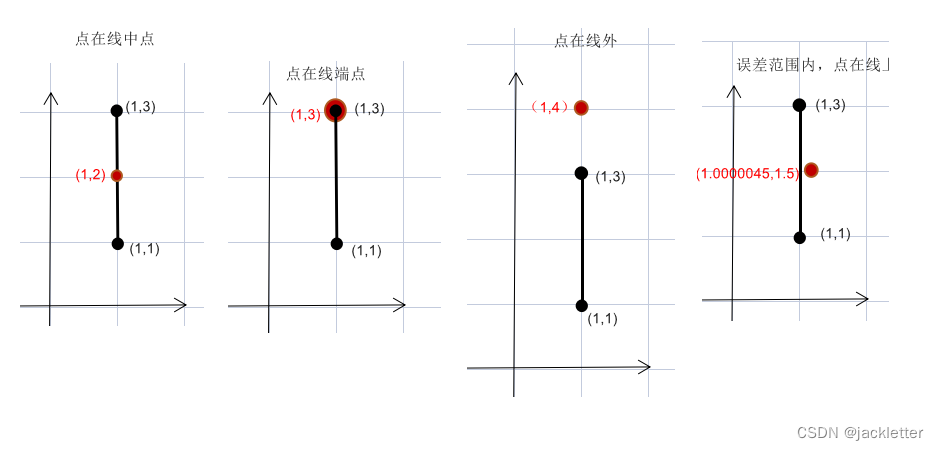
二、点与线关系

它们之间可能存在的关系：

• 点在线上（点在线中间、端点等特殊位置）
• 点不在线上

直接看下面封装的方法：

static (bool isPointOnLine, bool isPointOnLineStart, bool isPointOnLineEnd, bool isPointOnLineMid, Coordinate fixCoordinate) CalcPointOnLine(Coordinate coordinate, LineSegment lineSegment, double tolerance)
{
    var cs = lineSegment.ClosestPoint(coordinate);
    if (!cs.Equals2D(coordinate, tolerance: tolerance)) return (false, false, false, false, coordinate);
    bool isPointOnLine = true;
    bool isPointOnLineStart = false, isPointOnLineEnd = false, isPointOnLineMid = false;

    if (cs.Equals2D(lineSegment.P0)) isPointOnLineStart = true;
    if (cs.Equals2D(lineSegment.P1)) isPointOnLineEnd = true;
    if (cs.Equals2D(lineSegment.MidPoint)) isPointOnLineMid = true;

    return (isPointOnLine, isPointOnLineStart, isPointOnLineEnd, isPointOnLineMid, cs);
}

看下面测试的案例：

看代码：

//点在中点
var res = CalcPointOnLine(new Coordinate(1, 2), new LineSegment(new Coordinate(1, 1), new Coordinate(1, 3)), 0.0001);
//点在终点
var res2 = CalcPointOnLine(new Coordinate(1, 3), new LineSegment(new Coordinate(1, 1), new Coordinate(1, 3)), 0.0001);
//点在外面
var res3 = CalcPointOnLine(new Coordinate(1, 4), new LineSegment(new Coordinate(1, 1), new Coordinate(1, 3)), 0.0001);
//误差范围内 点在线上
var res4 = CalcPointOnLine(new Coordinate(1.0000045, 1.5), new LineSegment(new Coordinate(1, 1), new Coordinate(1, 3)), 0.0001);

vs调试效果：

三、线与线关系

线与线关系可大致分如下情况：

看封装的代码：

public enum EnumLineLineTouchType
{
    NoTouch,
    Join,
    TSharpIntersect,
    Cross,
    PartOverlap,
    Equal,
    Contain,
}
    
/// <summary>
/// tolerance: 这里有两个地方做容差, 当端点近似重合时; 当角度近似平行或垂直时
/// </summary>
static (EnumLineLineTouchType touchType, bool isParallel, bool isPerpendicular, Coordinate[] coordinates, LineSegment fixLineSegment1, LineSegment fixLineSegment2) CalcLineOnLine(LineSegment lineSegment1, LineSegment lineSegment2, double tolerancePosition, double toleranceAngelDegree)
{
    var line1 = lineSegment1;
    var line2 = new LineSegment(lineSegment2.P0, lineSegment2.P1);
    //先处理端点近似重合时的容差
    if (tolerancePosition > 0)
    {
        //端点重合时
        if (line2.P0.Equals2D(lineSegment1.P0, tolerancePosition)) line2.SetCoordinates(lineSegment1.P0, line2.P0);
        else if (line2.P0.Equals2D(lineSegment1.P1, tolerancePosition)) line2.SetCoordinates(lineSegment1.P0, line2.P1);
        if (line2.P1.Equals2D(lineSegment1.P0, tolerancePosition)) line2.SetCoordinates(line2.P0, lineSegment1.P0);
        else if (line2.P1.Equals2D(lineSegment1.P1, tolerancePosition)) line2.SetCoordinates(line2.P0, lineSegment1.P1);
    }
    //计算角度
    bool isParallel = false, isPerpendicular = false;
    //（-180,180]
    var line1Angel = AngleUtility.ToDegrees(AngleUtility.Normalize(line1.Angle));
    var line2Angel = AngleUtility.ToDegrees(AngleUtility.Normalize(line2.Angle));
    var diff = Math.Abs(line1Angel - line2Angel);
    if (diff % 180 <= toleranceAngelDegree)
    {
        isParallel = true;
        if (diff != 0)
        {
            //处理容差
            Vector2D v = null;
            if (diff > 90)
            {
                //反向平行
                v = new Vector2D(line1.P1, line1.P0).Normalize();
            }
            else
            {
                //同向平行
                v = new Vector2D(line1.P0, line1.P1).Normalize();
            }
            line2.SetCoordinates(line2.P0, new Coordinate(line2.P0.X + v.Multiply(line2.Length).X, line2.P0.Y + v.Multiply(line2.Length).Y));
        }
    }
    else if (diff % 90 <= toleranceAngelDegree)
    {
        isPerpendicular = true;
        if (diff != 0)
        {
            //处理容差
            Vector2D v = new Vector2D(line1.P0, line1.P1).Normalize();
            var v1 = new Vector2D(v.Y, -v.X);
            var v2 = new Vector2D(-v.Y, v.X);
            var v1Diff = Math.Abs(AngleUtility.Normalize(v1.Angle()) - AngleUtility.Normalize(line2.Angle));
            var v2Diff = Math.Abs(AngleUtility.Normalize(v2.Angle()) - AngleUtility.Normalize(line2.Angle));
            if (v1Diff < v2Diff)
            {
                v = v1;
            }
            else
            {
                v = v2;
            }
            line2.SetCoordinates(line2.P0, new Coordinate(line2.P0.X + v.Multiply(line2.Length).X, line2.P0.Y + v.Multiply(line2.Length).Y));
        }
    }

    //容差处理完毕
    //计算相交
    var t = new NetTopologySuite.Algorithm.RobustLineIntersector();
    t.ComputeIntersection(lineSegment1.P0, lineSegment1.P1, lineSegment2.P0, lineSegment2.P1);

    EnumLineLineTouchType? lineLineTouchType = null;
    Coordinate[] coordinates = null;
    if (t.IntersectionNum == 0)
    {
        lineLineTouchType = EnumLineLineTouchType.NoTouch;
        coordinates = new Coordinate[0];
    }
    else if (t.IntersectionNum == 1)
    {
        coordinates = new Coordinate[] { t.GetIntersection(0) };
        var isOnLine1EndPoint = coordinates[0].Equals2D(lineSegment1.P0) || coordinates[0].Equals2D(lineSegment1.P1);
        var isOnLine2EndPoint = coordinates[0].Equals2D(lineSegment2.P0) || coordinates[0].Equals2D(lineSegment2.P1);
        if (isOnLine1EndPoint && isOnLine2EndPoint)
        {
            lineLineTouchType = EnumLineLineTouchType.Join;
        }
        else if ((isOnLine1EndPoint && !isOnLine2EndPoint) || (!isOnLine1EndPoint && isOnLine2EndPoint))
        {
            lineLineTouchType = EnumLineLineTouchType.TSharpIntersect;
        }
        else if (!isOnLine1EndPoint && !isOnLine2EndPoint)
        {
            lineLineTouchType = EnumLineLineTouchType.Cross;
        }
    }
    else if (t.IntersectionNum == 2)
    {
        coordinates = new Coordinate[] { t.GetIntersection(0), t.GetIntersection(1) };
        var c1Line1 = CalcPointOnLine(coordinates[0], lineSegment1, 0);
        var c1OnLine1EndPoint = c1Line1.isPointOnLineStart || c1Line1.isPointOnLineEnd;

        var c1Line2 = CalcPointOnLine(coordinates[0], lineSegment2, 0);
        var c1OnLine2EndPoint = c1Line2.isPointOnLineStart || c1Line2.isPointOnLineEnd;

        var c2Line1 = CalcPointOnLine(coordinates[1], lineSegment1, 0);
        var c2OnLine1EndPoint = c2Line1.isPointOnLineStart || c2Line1.isPointOnLineEnd;

        var c2Line2 = CalcPointOnLine(coordinates[1], lineSegment2, 0);
        var c2OnLine2EndPoint = c2Line2.isPointOnLineStart || c2Line2.isPointOnLineEnd;

        if (c1OnLine1EndPoint && c2OnLine1EndPoint && c1OnLine2EndPoint && c2OnLine2EndPoint)
        {
            //相等
            lineLineTouchType = EnumLineLineTouchType.Equal;
        }
        else if ((c1OnLine1EndPoint ^ c2OnLine1EndPoint) && (c1OnLine2EndPoint ^ c2OnLine2EndPoint))
        {
            //部分重合
            lineLineTouchType = EnumLineLineTouchType.PartOverlap;
        }
        else if (
            ((c1OnLine1EndPoint & c2OnLine1EndPoint) && ((c1OnLine2EndPoint & c2OnLine2EndPoint) == false))//c2包含c1
            || (((c1OnLine1EndPoint & c2OnLine1EndPoint) == false) && (c1OnLine2EndPoint & c2OnLine2EndPoint))//c1包含c2
            )
        {
            //包含
            lineLineTouchType = EnumLineLineTouchType.Contain;
        }
    }
    return (lineLineTouchType!.Value, isParallel, isPerpendicular, coordinates!, line1, line2);
}

看测试效果：

static void Main(string[] args)
{
    //相离
    var res1 = CalcLineOnLine(new LineSegment(new Coordinate(0, 0), new Coordinate(0, 2)), new LineSegment(new Coordinate(3, 0), new Coordinate(2, 2)), 0, 0);
    //相接
    var res2 = CalcLineOnLine(new LineSegment(new Coordinate(0, 0), new Coordinate(0, 2)), new LineSegment(new Coordinate(3, 0), new Coordinate(0, 2)), 0, 0);
    //丁字相交
    var res3 = CalcLineOnLine(new LineSegment(new Coordinate(0, 0), new Coordinate(0, 2)), new LineSegment(new Coordinate(3, 0), new Coordinate(0, 1)), 0, 0);
    //十字相交
    var res4 = CalcLineOnLine(new LineSegment(new Coordinate(0, 0), new Coordinate(0, 2)), new LineSegment(new Coordinate(1, 0), new Coordinate(-1, 2)), 0, 0);
    //部分重合
    var res5 = CalcLineOnLine(new LineSegment(new Coordinate(0, 0), new Coordinate(0, 2)), new LineSegment(new Coordinate(0, 1), new Coordinate(0, -1)), 0, 0);
    //相等
    var res6 = CalcLineOnLine(new LineSegment(new Coordinate(0, 0), new Coordinate(0, 2)), new LineSegment(new Coordinate(0, 0), new Coordinate(0, 2)), 0, 0);
    //包含1
    var res7 = CalcLineOnLine(new LineSegment(new Coordinate(0, 0), new Coordinate(0, 2)), new LineSegment(new Coordinate(0, 0), new Coordinate(0, 1)), 0, 0);
    //包含2
    var res8 = CalcLineOnLine(new LineSegment(new Coordinate(0, 0), new Coordinate(0, 2)), new LineSegment(new Coordinate(0, -1), new Coordinate(0, 3)), 0, 0);

    //端点容差
    var res9 = CalcLineOnLine(new LineSegment(new Coordinate(0, 0), new Coordinate(0, 2)), new LineSegment(new Coordinate(0, 1), new Coordinate(0, 2.00000456)), 0.0001, 0);
    //角度容差
    var res10 = CalcLineOnLine(new LineSegment(new Coordinate(0, 0), new Coordinate(0, 2)), new LineSegment(new Coordinate(0, 1), new Coordinate(0.00000456, 2)), 0, 0.1);
    
    Console.ReadLine();
}

四、线与面关系

种类较多，如下图：

探索线面相交、相减。。。

4.1 线面相交

上面几种关系相交的测试：

var polygon = new Polygon(new LinearRing(new Coordinate[]
{
    new Coordinate(2,0),
    new Coordinate(2,4),
    new Coordinate(3,4),
    new Coordinate(3,2),
    new Coordinate(4,2),
    new Coordinate(4,4),
    new Coordinate(5,4),
    new Coordinate(5,0),
    new Coordinate(2,0),
}));
//相离
var g1 = polygon.Intersection(new LineString(new[] { new Coordinate(1, 1), new Coordinate(1, 4) }));
//相切
var g2 = polygon.Intersection(new LineString(new[] { new Coordinate(1, 1), new Coordinate(3, -1) }));
//相接
var g3 = polygon.Intersection(new LineString(new[] { new Coordinate(1, 1), new Coordinate(2, 0) }));
//包含
var g4 = polygon.Intersection(new LineString(new[] { new Coordinate(3, 1), new Coordinate(4, 1) }));

//相交1
var g5 = polygon.Intersection(new LineString(new[] { new Coordinate(1, 1), new Coordinate(6, 1) }));
//相交2
var g6 = polygon.Intersection(new LineString(new[] { new Coordinate(1, 2), new Coordinate(6, 2) }));
//相交3
var g7 = polygon.Intersection(new LineString(new[] { new Coordinate(1, 1), new Coordinate(4, 1) }));
//相交4
var g8 = polygon.Intersection(new LineString(new[] { new Coordinate(1, 3), new Coordinate(4.5, 3) }));

//与边重合
var g9 = polygon.Intersection(new LineString(new[] { new Coordinate(2, 1), new Coordinate(2, 2) }));
var g10 = polygon.Intersection(new LineString(new[] { new Coordinate(2, 3), new Coordinate(2, 5) }));
var g11 = polygon.Intersection(new LineString(new[] { new Coordinate(2, 0), new Coordinate(2, 4) }));

Console.ReadLine();

可以看到，线面相交的结果可能是空或者是点、线的组合，但不可能是面。

4.2 线面相减

将上面相交的所有改成var g1 = polygon.Difference(new LineString(new[] { new Coordinate(1, 1), new Coordinate(1, 4) }));这种形式，得到的运算结果如下：

可以看到，面减去线的结果就是将交点加入的面的轮廓中去，这个面的整体形状不会有任何改变！
这好像没什么有用的信息。

4.3 用线切割面

现在想实现一种效果，即: 让一条线段去切割多边形，那么可能切成0、1、n个多边形，对应的切线段也可能有多个。

比如上面的几种相交关系：

• 相交1 到 相交4 分别切出2个、3个、0个、2个多边形，对应的切线段有1个、2个、0个、1个；
• 其他的如，相离、相切、包含、与边重合等都不能切；

针对这种需求，封装如下代码：

/// <summary>
/// 使用一条线切割多边形,可得到多个切线端和多个多边形
/// </summary>
static (Polygon[] polygons, LineSegment[] lineSegments) SplitPolygonByLine(Polygon polygon, LineSegment lineSegment)
{
    var lineClip = new LineString(new[] { lineSegment.P0, lineSegment.P1 });
    var g = polygon.Intersection(lineClip);
    if (g is Point point) return (new[] { polygon }, new LineSegment[0]);
    if (g is MultiPoint multiPoint) return (new[] { polygon }, new LineSegment[0]);

    var lines = new List<LineSegment>();
    if (g is LineString lineString)
    {
        if (lineString.Count > 0) lines.Add(new LineSegment(lineString.Coordinates[0], lineString.Coordinates[1]));
    }
    if (g is MultiLineString multiLineString)
    {
        foreach (var item in multiLineString.Geometries)
        {
            var tmp = item as LineString;
            if (tmp.Count > 0) lines.Add(new LineSegment(tmp.Coordinates[0], tmp.Coordinates[1]));
        }
    }
    if (lines.Count == 0) return (new[] { polygon }, new LineSegment[0]);
    //进行切割
    var g2 = polygon.SymmetricDifference(lineClip);
    var pointPolygon = g2 as Polygon;
    if (pointPolygon == null)
    {
        var coll = g2 as GeometryCollection;
        pointPolygon = coll!.Where(i => i is Polygon).FirstOrDefault() as Polygon;
    }
    var polygons = new List<Polygon>() { pointPolygon! };

    for (int i = lines.Count - 1; i >= 0; i--)
    {
        var line = lines[i];
        var hasFind = false;
        for (int j = 0; j < polygons.Count; j++)
        {
            var tmpPolygon = polygons[j];
            var cs = tmpPolygon.Coordinates.ToList();
            var startIndex = cs.FindIndex(i => i.Equals2D(line.P0));
            var endIndex = cs.FindIndex(i => i.Equals2D(line.P1));
            if (startIndex != -1 && endIndex != -1 && Math.Abs(startIndex - endIndex) == 1)
            {
                //和 tmpPolygon 的边重合,直接舍弃
                break;
            }
            if (startIndex != -1 && endIndex != -1 && Math.Abs(startIndex - endIndex) > 1)
            {
                //在这个 tmpPolygon 上找到了交点
                //分离两个polygon
                if (startIndex > endIndex)
                {
                    var t = startIndex;
                    startIndex = endIndex;
                    endIndex = t;
                }
                //一个
                var tmpCs = cs.Skip(startIndex).Take(endIndex - startIndex + 1).ToList();
                tmpCs.Add(tmpCs[0]);
                //二个
                var tmpCs2 = cs.Skip(endIndex).SkipLast(1).ToList();
                tmpCs2.AddRange(cs.Take(startIndex + 1));
                tmpCs2.Add(tmpCs2[0]);

                polygons.RemoveAt(j);
                polygons.Add(new Polygon(new LinearRing(tmpCs.ToArray())));
                polygons.Add(new Polygon(new LinearRing(tmpCs2.ToArray())));

                lines[i].SetCoordinates(cs[startIndex], cs[endIndex]);
                hasFind = true;
                break;
            }
        }
        if (!hasFind) lines.RemoveAt(i);
    }

    return (polygons.ToArray(), lines.ToArray());
}

针对上面几种相交关系的测试如下：

var polygon = new Polygon(new LinearRing(new Coordinate[]
{
    new Coordinate(2,0),
    new Coordinate(2,4),
    new Coordinate(3,4),
    new Coordinate(3,2),
    new Coordinate(4,2),
    new Coordinate(4,4),
    new Coordinate(5,4),
    new Coordinate(5,0),
    new Coordinate(2,0),
}));
//相离
var res1 = SplitPolygonByLine(polygon, new LineSegment(new Coordinate(1, 1), new Coordinate(1, 4)));
//相切
var res2 = SplitPolygonByLine(polygon, new LineSegment(new Coordinate(1, 1), new Coordinate(3, -1)));
//相接
var res3 = SplitPolygonByLine(polygon, new LineSegment(new Coordinate(1, 1), new Coordinate(2, 0)));
//包含
var res4 = SplitPolygonByLine(polygon, new LineSegment(new Coordinate(3, 1), new Coordinate(4, 1)));

//相交1
var res5 = SplitPolygonByLine(polygon, new LineSegment(new Coordinate(1, 1), new Coordinate(6, 1)));
//相交2
var res6 = SplitPolygonByLine(polygon, new LineSegment(new Coordinate(1, 2), new Coordinate(6, 2)));
//相交3
var res7 = SplitPolygonByLine(polygon, new LineSegment(new Coordinate(1, 1), new Coordinate(4, 1)));
//相交4
var res8 = SplitPolygonByLine(polygon, new LineSegment(new Coordinate(1, 3), new Coordinate(4.5, 3)));

//与边重合
var res9 = SplitPolygonByLine(polygon, new LineSegment(new Coordinate(2, 1), new Coordinate(2, 2)));
var res10 = SplitPolygonByLine(polygon, new LineSegment(new Coordinate(2, 3), new Coordinate(2, 5)));
var res11 = SplitPolygonByLine(polygon, new LineSegment(new Coordinate(2, 0), new Coordinate(2, 4)));

效果如下：

可以从切出的多边形和切线段数量大致看到效果。

为了验证，再看一种复杂的图形切割如下：

图上这条红色的线段将多边形切成了4块，同时产生的切线段有3条，测试代码如下：

var complexPolygon = new Polygon(new LinearRing(new Coordinate[]
{
    new Coordinate(2,0),
    new Coordinate(2,5),
    new Coordinate(5,5),
    new Coordinate(5,2),
    new Coordinate(4,2),
    new Coordinate(4,4),
    new Coordinate(3,4),
    new Coordinate(3,1),
    new Coordinate(6,1),
    new Coordinate(6,5),
    new Coordinate(7,5),
    new Coordinate(7,1),
    new Coordinate(8,1),
    new Coordinate(8,5),
    new Coordinate(9,5),
    new Coordinate(9,0),
    new Coordinate(2,0),
}));
var res12 = SplitPolygonByLine(complexPolygon, new LineSegment(new Coordinate(1, 3), new Coordinate(8.5, 3)));

调试效果：

五、面与面关系

面与面的关系比较复杂，如下：

可以从面面运算中观察规律。。。

5.1 面面相交

面面相交可能为空也可能是 点、线、面的集合。
以下面两个图形做测试：

看测试代码：

varg1 = new Polygon(new LinearRing(new[]
{
    new Coordinate(5, 1),
    new Coordinate(5, 5),
    new Coordinate(9, 5),
    new Coordinate(9, 1),
    new Coordinate(5, 1),
})).Intersection(new Polygon(new LinearRing(new[]
{
    new Coordinate(1, 1),
    new Coordinate(1, 4),
    new Coordinate(4, 4),
    new Coordinate(4, 1),
    new Coordinate(1, 1),
})));
var g2 = new Polygon(new LinearRing(new[]
{
    new Coordinate(3, 2),
    new Coordinate(3, 6),
    new Coordinate(7, 6),
    new Coordinate(7, 2),
    new Coordinate(3, 2),
})).Intersection(new Polygon(new LinearRing(new[]
{
    new Coordinate(1, 1),
    new Coordinate(1, 8),
    new Coordinate(8, 8),
    new Coordinate(8, 4),
    new Coordinate(6, 4),
    new Coordinate(6, 7),
    new Coordinate(5, 7),
    new Coordinate(5, 6),
    new Coordinate(4, 6),
    new Coordinate(4, 7),
    new Coordinate(2, 7),
    new Coordinate(2, 2),
    new Coordinate(3, 2),
    new Coordinate(3, 1),
    new Coordinate(1, 1),
})));

调试效果：

结果： 第一个显然为空，第二个相交得1点、1线、1面

5.2 面面相减

还是以上面两个图形为例，将Intersection换成Difference

调试效果：

结果： 第一个仍然为黑色矩形，因为相交为空，第二个是黑色矩形减去相交后的形状

5.3 面面相加

还是使用上面的图形，将Intersection换成Union
调试结果：

结果： 第一个因为两个矩形不相接，直接成了MultiPolygon，第二个是变成了外围轮廓挖去两个洞

再看看下面相接的情况：

它们Union代码：

var g3 = new Polygon(new LinearRing(new[]
{
    new Coordinate(3, 2),
    new Coordinate(3, 6),
    new Coordinate(7, 6),
    new Coordinate(7, 2),
    new Coordinate(3, 2),
})).Union(new Polygon(new LinearRing(new[]
{
    new Coordinate(3, 2),
    new Coordinate(3, 6),
    new Coordinate(1, 6),
    new Coordinate(1, 2),
    new Coordinate(3, 2),
})));

调试效果：

显然，它取了外围轮廓。

六、点与面关系

很显然，点可以在面外、面内、面的顶点上、面的边上。
封装方法如下：

/// <summary>
/// 点是否在面上
/// </summary>
public static (bool isOnPolygon, bool isOnEdge, bool isOnCorner, Coordinate fixCoordinate) CalcPointOnPolygon(Polygon polygon, Coordinate coordinate, double tolerance)
{
    var fixCoordinate = coordinate.Copy();
    var p = new Point(coordinate.X, coordinate.Y);
    var cs = polygon.Shell.Coordinates;
    var arr = cs.SkipLast(1).ToList();
    var isOnPolygon = false; var isOnEdge = false; var isOnCorner = false;
    //先处理端点容差
    for (int i = 0; i < arr.Count; i++)
    {
        var p1 = arr[i];
        if (p1.Equals2D(coordinate, tolerance))
        {
            isOnPolygon = isOnEdge = isOnCorner = true;
            fixCoordinate = p1.Copy();
            break;
        }
    }
    //处理边容差
    for (int i = 0; i < arr.Count; i++)
    {
        var p1 = arr[i];
        var p2 = arr[(i + 1 + arr.Count) % arr.Count];
        (bool isPointOnLine, bool isPointOnLineStart, bool isPointOnLineEnd, bool isPointOnLineMid, Coordinate tmp) = CalcPointOnLine(coordinate, new LineSegment(p1, p2), tolerance);
        if (isPointOnLine)
        {
            isOnPolygon = isOnEdge = true;
            fixCoordinate = tmp.Copy();
        }
    }
    //是否在面内
    var g = polygon.Intersection(p) as Point;
    if (!g.IsEmpty) isOnPolygon = true;
    return (isOnPolygon, isOnEdge, isOnCorner, fixCoordinate);
}

测试代码如下：

//点在面上
var polygon = new Polygon(new LinearRing(new Coordinate[]
{
    new Coordinate(2,0),
    new Coordinate(2,2),
    new Coordinate(4,2),
    new Coordinate(4,0),
    new Coordinate(2,0),
}));

//不接触
var res1 = FunctionLib.CalcPointOnPolygon(polygon, new Coordinate(1, 1), 0);
//在角上
var res2 = FunctionLib.CalcPointOnPolygon(polygon, new Coordinate(2, 2), 0);
//在内部
var res3 = FunctionLib.CalcPointOnPolygon(polygon, new Coordinate(3, 1), 0);
//在线上
var res4 = FunctionLib.CalcPointOnPolygon(polygon, new Coordinate(2, 1), 0);

//容差内角上
var res5 = FunctionLib.CalcPointOnPolygon(polygon, new Coordinate(2, 2.0000568), 0.0001);
//容差内线上
var res6 = FunctionLib.CalcPointOnPolygon(polygon, new Coordinate(1.9999999123, 1), 0.0001);

调试效果：