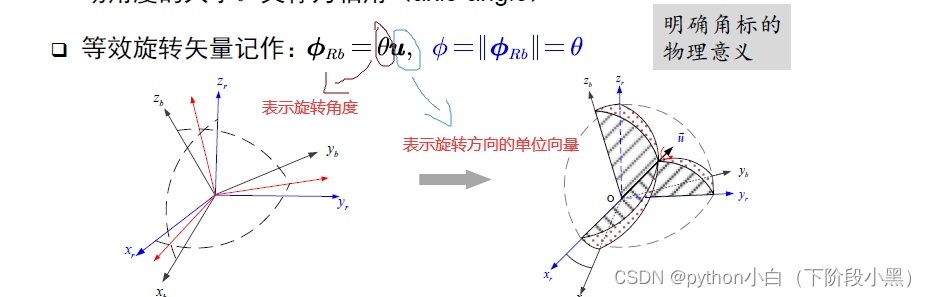
惯性导航算法(五)-等效旋转矢量+双子样算法
文章目录等效旋转矢量转动的不可交换性转动的不可交换性与惯性导航有何关系?等效旋转矢量等效旋转矢量多子样算法的理论基础等效旋转矢量微分方程等效旋转矢量微分方程的工程近似等效旋转矢量的双子样算法等效旋转矢量转动的不可交换性力学中刚体的有限次转动是不可交换的。转动的不可交换性决定了转动不是矢量,即两次以上的不同轴转动不能相加。对一个空间方向随时间变化的角速度矢量进行积分是没有物理意义的上图两个极端的例子
等效旋转矢量
转动的不可交换性
力学中刚体的有限次转动是不可交换的。转动的不可交换性
决定了转动不是矢量,即两次以上的不同轴转动不能相加。
对一个空间方向随时间变化的角速度矢量进行积分是没有物
理意义的

上图两个极端的例子说明,不能根据陀螺输出的角增量来判断实际的姿态变化,因为姿态变化具有不可交换性,不但要知道角增量,还要知道旋转过程是怎样的,才能确定姿态变化;也就是说角度增量不靠谱(Case1和Case2最终姿态不同,但是角增量却相等),因此就要引入等效旋转矢量,他是一个定轴旋转,Case1和Case2对应的等效旋转矢量就肯定是不同的了,也就是确定性的量
转动的不可交换性与惯性导航有何关系?
陀螺在输出角增量时只对各轴的角度变化量做了数值累加,
并未考虑角速度Wib向量在采样间隔内的方向变化,因此陀
螺角增量输出没有明确的物理含义。

等效旋转矢量
1.理论基础:一个坐标系到另一个坐标系的变换可以通过多次
转动来完成,也可以通过绕一个定义在参考坐标系中的矢量
的单次转动来实现。
2.该矢量称作等效旋转矢量(rotation vector)是一个三元素的
向量,旋转矢量的方向给出了转动轴的方向,它的模长为转
动角度的大小。又称为轴角(axis-angle)

等效旋转矢量表示两个坐标系间的转动关系,可转换为对应的方向余弦矩阵和姿态四元数,完成姿态更新
1.Rodrigues 旋转公式

2.姿态四元数的三角函数式

3.满足DCM(方向余弦矩阵)和四元数微分方程求解所要求的“定轴旋转”条件,理论上可完美补偿不可交换性误差。
注:问题的关键在于如何利用陀螺输出构造等效旋转矢量。
等效旋转矢量多子样算法的理论基础
1969年,John E. Bortz在其博士论文中详细推导了等效旋转矢量微分方程(Bortz方程),该方程是利用陀螺输出求解等效旋转矢量的基本公式,奠定了等效旋转矢量多子样算法的理论基础。
等效旋转矢量微分方程
可用几何的方法或根据四元数的微分方程来推导等效旋
转矢量的微分方程式,即Bortz 方程

1.等效旋转矢量常用于表示姿态的变化量。
2.Bortz方程等式右边两项补偿了角速度向量的方向变化

3.如果真的旋转过程是定轴旋转的话,那么角速度与旋转的角度变化肯定平行,那么叉乘为0,后两项都为0,这样Bortz方程就退化成了我们之前直观以为的,角度变化的微分就等于角速度
等效旋转矢量微分方程的工程近似

注:这里是做了—个近似,将等效旋转矢量替换为角度增量,因为等效旋转矢量是小量,它和角度增量又是—个微小的差异,因此这个差异就是二阶小量,可以忽略
等效旋转矢量的双子样算法
因为姿态更新用到了两个历元的角增量,因此叫双子样算法

由上图可得角速度表达式(我们假设角速度变化是线性的(原来我们认为角速度方向不变),而不再是之前定轴假设的不变量),角增量表达式可由下图推导出:


由上图可知,我们之前的定轴假设实际上就是把二阶圆锥误差补偿项给漏掉了;之所以叫二阶圆锥误差补偿,是因为当载体做圆锥运动的时候,这一项显得格外突出,因此而命名

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献17条内容
已为社区贡献17条内容





所有评论(0)