大模型推理优化技术-KV Cache
KV Cache 是大模型推理性能优化的一个常用技术,该技术可以在不影响任何计算精度的前提下,通过空间换时间的思想,提高推理性能。本文简要分析了 KV Cache 原理、源码以及计算量和显存占用,这是一种典型的通过空间换时间(计算)的技术,虽然并不复杂,但是现在基本上是仅编码器Transformer架构生成大语言模型必备优化技术。
近两年大模型火出天际;同时,也诞生了大量针对大模型的优化技术。本系列将针对一些常见大模型优化技术进行讲解。
- 大模型推理优化技术-KV Cache
- 大模型显存优化技术-PagedAttention
- 大模型显存I/O优化技术-FlashAttention V1
- 大模型推理优化技术-Flash-Decoding
- 大模型显存优化技术-ZeRO系列
- 大模型解码优化-Speculative Decoding及其变体
- 大模型推理服务化调度优化技术-Dynamic batching/Continuous batching
而本文将针对仅编码器Transformer架构(Decoder-Only Transformer)的模型必备显存优化技术 KV Cache 进行讲解。

KV Cache 简介
KV Cache 是大模型推理性能优化的一个常用技术,该技术可以在不影响任何计算精度的前提下,通过空间换时间的思想,提高推理性能。
KV Cache 诞生的背景
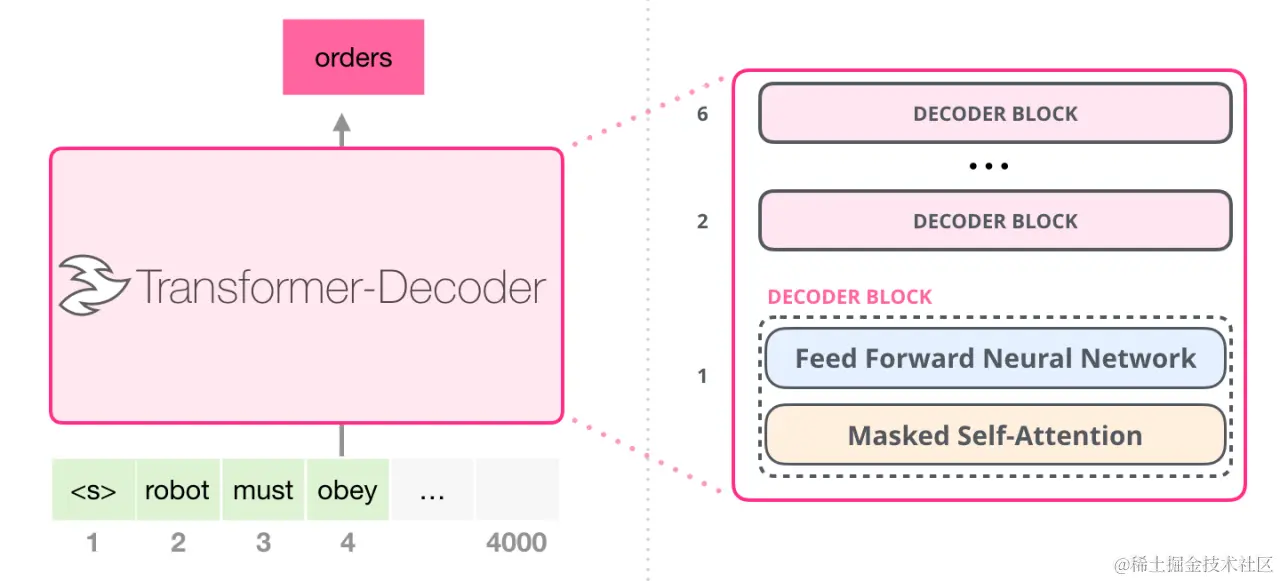
对于仅编码器Transformer架构的模型的推理,我们给一个输入文本,模型会输出一个回答(长度为 N),其实该过程中执行了 N 次推理过程。即类 GPT 的仅编码器模型一次推理只输出一个token,输出的 token 会与输入 tokens 拼接在一起,然后作为下一次推理的输入,这样不断反复直到遇到终止符。
针对一个仅编码器Transformer架构的模型,假设用户输入为“recite the first law”,模型续写得到的输出为“A robot may not ”,模型的生成过程如下:
- 将“ecite the first law”输入模型,得到每个token的注意力表示。使用“law”的注意力表示,预测得到下一个token为“A”(实际还需要将该注意力表示映射成概率分布logits,为了方便叙述,我们忽略该步骤)。
- 将“A”拼接到原来的输入,得到“recite the first law A”,将其输入模型,得到注意力表示,使用“A”的注意力表示,预测得到下一个token为“robot”。
- 将“robot”拼接到原来的输入,依此类推,预测得到“robot”,最终得到“recite the first law A robot may not”

仅编码器Transformer架构的自回归模型为带 Masked 的 Self Attention。因此,在没有KV Cache的情况下,其计算过程如下所示。

正常情况下,Attention的计算公式如下:

为了看上去方便,我们暂时忽略scale项,因此,Attention的计算公式如下所示(softmaxed 表示已经按行进行了softmax):


当QKTQK^TQKT变为矩阵时,softmax 会针对行进行计算,详细如下(softmaxed 表示已经按行进行了softmax):

其中,Att1(Q,K,V)Att_1(Q,K,V)Att1(Q,K,V)表示 Attention 的第一行, Att2(Q,K,V)Att_2(Q,K,V)Att2(Q,K,V)表示 Attention 的第二行。

对于Att1(Q,K,V)Att_1(Q,K,V)Att1(Q,K,V),由于Q1K2TQ_1K_2^TQ1K2T这个值会mask掉,你会发现,Q1Q_1Q1 在第二步参与的计算与第一步是完全一样的,并且 V1V_1V1 参与计算Attention时也仅仅依赖于 Q1Q_1Q1 ,与 Q2Q_2Q2 毫无关系。
对于Att2(Q,K,V)Att_2(Q,K,V)Att2(Q,K,V),V2V_2V2 参与计算Attention时也仅仅依赖于Q2Q_2Q2 ,与 Q1Q_1Q1 毫无关系。

其计算方式如 Step2 所示。


其计算方式如 Step2 所示。

对于Attk(Q,K,V)Att_k(Q,K,V)Attk(Q,K,V), VkV_kVk 参与计算Attention时也仅仅依赖于 QkQ_kQk。
看上面图和公式,我们可以得出以下结论:
- 当前计算方式存在大量冗余计算,每一次生成新的Token都需要计算之前的KV。
- Attk(Q,K,V)Att_k(Q,K,V)Attk(Q,K,V)的计算过程中,主要与 QkQ_kQk 有关。VkV_kVk 参与计算Attention时也仅仅依赖于 QkQ_kQk。
- 每一步中,其实只需要根据QkQ_kQk 计算 Attk(Q,K,V)Att_k(Q,K,V)Attk(Q,K,V) 就可以,之前已经计算的Attention完全不需要重新计算。但是 K 和 V 是全程参与计算的,所以这里我们需要把每一步的 K 、 V 缓存起来。
KV Cache 步骤
正是因为 Self Attention 中带 Masked ,因此,在推理的时候,前面已经生成的 Token 不需要与后面的 Token 产生 Attention ,从而使得前面已经计算的 K 和 V 可以缓存起来。
一个典型的带有 KV cache 优化的生成大模型的推理过程包含了两个阶段:
-
预填充阶段:输入一个prompt序列,为每个transformer层生成 key cache 和 value cache(KV cache)。
-
解码阶段:使用并更新KV cache,一个接一个地生成token,当前生成的token词依赖于之前已经生成的token。
预填充阶段计算过程如下:

解码阶段计算过程如下:

使不使用 KV Cache 的对比
下图展示了使用KV Cache和不使用KV Cache的对比,其中,紫色部分表示从缓存获取,灰色部分表示会被Masked。




下面使用 transformers 来比较有 KV Cache 和没有 KV Cache的情况下,GPT-2的生成速度。
import numpy as np
import time
import torch
from transformers import AutoModelForCausalLM, AutoTokenizer
device = "cuda" if torch.cuda.is_available() else "cpu"
tokenizer = AutoTokenizer.from_pretrained("gpt2")
model = AutoModelForCausalLM.from_pretrained("gpt2").to(device)
for use_cache in (True, False):
times = []
for _ in range(10): # measuring 10 generations
start = time.time()
model.generate(**tokenizer("What is KV caching?", return_tensors="pt").to(device), use_cache=use_cache, max_new_tokens=1000)
times.append(time.time() - start)
print(f"{'with' if use_cache else 'without'} KV caching: {round(np.mean(times), 3)} +- {round(np.std(times), 3)} seconds")
运行结果:
- 使用 KV caching: 11.885 ± 0.272 秒
- 不使用 KV caching: 56.197 ± 1.855 秒
可以看到使不使用 KV cache 推理性能果差异显存。
使用 KV Cache 解码阶段计算量分析
FLOPs,floating point operations,表示浮点数运算次数,衡量了计算量的大小。
如何计算矩阵乘法的FLOPs呢?
对于 𝐴∈𝑅1×𝑛,𝐵∈𝑅𝑛×1𝐴∈𝑅{1×𝑛},𝐵∈𝑅{𝑛×1}A∈R1×n,B∈Rn×1 ,计算 𝐴𝐵 需要进行 𝑛 次乘法运算和 𝑛 次加法运算,共计 2𝑛 次浮点数运算,需要 2𝑛2𝑛2n 的FLOPs。对于 𝐴∈𝑅𝑚×𝑛,𝐵∈𝑅𝑛×𝑝𝐴∈𝑅{𝑚×𝑛},𝐵∈𝑅{𝑛×𝑝}A∈Rm×n,B∈Rn×p ,计算 𝐴𝐵 需要的浮点数运算次数为 m∗2n∗p=2𝑚𝑛𝑝m*2n*p=2𝑚𝑛𝑝m∗2n∗p=2mnp 。
下面来看看在一个 Token 生成过程中一层 Transformer 的计算量。
首先,分析 self-attention 块的计算,计算公式如下:
𝑄=𝑥𝑊𝑄,𝐾=𝑥𝑊𝐾,𝑉=𝑥𝑊𝑉𝑄=𝑥𝑊_𝑄,𝐾=𝑥𝑊_𝐾,𝑉=𝑥𝑊_𝑉Q=xWQ,K=xWK,V=xWV
𝑥𝑜𝑢𝑡=softmax(𝑄𝐾𝑇h)⋅𝑉⋅𝑊O+x𝑥_{𝑜𝑢𝑡}=softmax(\frac {𝑄𝐾^𝑇}{\sqrt h})⋅𝑉⋅𝑊_O+xxout=softmax(hQKT)⋅V⋅WO+x
我们来看看不使用 KV Cache 时,假设输入数据的形状为 [b, s],隐藏层维度为 h,则输入的形状为 [b, s, h]。self-attention块的计算如下:
- 计算 𝑄,𝐾,𝑉 :矩阵乘法的输入和输出形状为
[𝑏,𝑠,ℎ]×[ℎ,ℎ]→[𝑏,𝑠,ℎ]。计算量为 3∗bs∗2h∗h=3∗2𝑏𝑠h2=6𝑏𝑠h2 3* bs*2h*h = 3∗2𝑏𝑠ℎ2=6𝑏𝑠ℎ23∗bs∗2h∗h=3∗2bsh2=6bsh2 。 - 𝑄𝐾𝑇𝑄𝐾^𝑇QKT 矩阵乘法的输入和输出形状为
[𝑏,ℎ𝑒𝑎𝑑_𝑛𝑢𝑚, 𝑠, 𝑝𝑒𝑟_ℎ𝑒𝑎𝑑_ℎ𝑖𝑑𝑑𝑒𝑛_𝑠𝑖𝑧𝑒]×[𝑏, ℎ𝑒𝑎𝑑_𝑛𝑢𝑚, 𝑝𝑒𝑟_ℎ𝑒𝑎𝑑_ℎ𝑖𝑑𝑑𝑒𝑛_𝑠𝑖𝑧𝑒, 𝑠]→[𝑏, ℎ𝑒𝑎𝑑_𝑛𝑢𝑚, 𝑠, 𝑠],计算量为 bs∗2h∗s=2bs2hbs*2h*s=2bs^2hbs∗2h∗s=2bs2h。 - 计算在 𝑉 上的加权 𝑠𝑐𝑜𝑟𝑒⋅𝑉 ,矩阵乘法的输入和输出形状为
[𝑏,ℎ𝑒𝑎𝑑_𝑛𝑢𝑚,𝑠,𝑠]×[𝑏,ℎ𝑒𝑎𝑑_𝑛𝑢𝑚,𝑠,𝑝𝑒𝑟_ℎ𝑒𝑎𝑑_ℎ𝑖𝑑𝑑𝑒𝑛_𝑠𝑖𝑧𝑒]→[𝑏,ℎ𝑒𝑎𝑑_𝑛𝑢𝑚,𝑠,𝑝𝑒𝑟_ℎ𝑒𝑎𝑑_ℎ𝑖𝑑𝑑𝑒𝑛_𝑠𝑖𝑧𝑒]。计算量为 bs∗2s∗h=2bs2hbs*2s*h=2bs^2hbs∗2s∗h=2bs2h 。 - attention后的线性映射,矩阵乘法的输入和输出形状为
[𝑏,𝑠,ℎ]×[ℎ,ℎ]→[𝑏,𝑠,ℎ]。计算量为 2𝑏𝑠h22𝑏𝑠ℎ^22bsh2 。
不使用 KV Cache 时,输入的形状为 [b, 1, h ],kv cache中含有 𝑘𝑣𝑙𝑒𝑛𝑔𝑡h𝑘𝑣_{𝑙𝑒𝑛𝑔𝑡ℎ}kvlength 个 past word。self-attention块的计算如下:
- 计算 𝑄,𝐾,𝑉𝑄,𝐾,𝑉Q,K,V :矩阵乘法的输入和输出形状为
[𝑏, 1, ℎ]×[ℎ, ℎ]→[𝑏, 1, ℎ]。计算量为 3∗b∗2h∗h=3∗2bh2=6bh23*b*2h*h=3*2bh2=6bh23∗b∗2h∗h=3∗2bh2=6bh2 。 - 𝑄𝐾𝑇𝑄𝐾^𝑇QKT 矩阵乘法的输入和输出形状为
[b, head_num, 1, per_head_hidden_size]×[b, head_num, per_head_hidden_size, kv_length+1]→[b, head_num, 1, kv_length+1]。计算量为 𝑏∗2h∗(𝑘𝑣𝑙𝑒𝑛𝑔𝑡h+1)=2b(kv𝑙𝑒𝑛𝑔𝑡h+1)h𝑏 * 2h * (𝑘𝑣_{𝑙𝑒𝑛𝑔𝑡ℎ}+1) = 2b(kv_{𝑙𝑒𝑛𝑔𝑡ℎ}+1)ℎb∗2h∗(kvlength+1)=2b(kvlength+1)h 。 - 计算在𝑉上的加权 𝑠𝑐𝑜𝑟𝑒·𝑉 ,矩阵乘法的输入和输出形状为
[b, head_num, 1, kv_length+1]×[b,head_num,kv_length+1,per_head_hidden_size]→[b,head_num,1,per_head_hidden_size]。计算量为 2𝑏(𝑘𝑣𝑙𝑒𝑛𝑔𝑡h+1)h2𝑏(𝑘𝑣_{𝑙𝑒𝑛𝑔𝑡ℎ}+1)ℎ2b(kvlength+1)h 。 - attention后的线性映射,矩阵乘法的输入和输出形状为
[𝑏,1,ℎ]×[ℎ,ℎ]→[𝑏,1,ℎ]。计算量为 2bh22bh^22bh2 。
接下来分析MLP块的计算,计算公式如下:
𝑥=𝑓𝑔𝑒𝑙𝑢(𝑥𝑜𝑢𝑡𝑊1)𝑊2+𝑥𝑜𝑢𝑡𝑥=𝑓_{𝑔𝑒𝑙𝑢}(𝑥_{𝑜𝑢𝑡}𝑊_1)𝑊_2+𝑥_{𝑜𝑢𝑡}x=fgelu(xoutW1)W2+xout
不使用 KV Cache 时:
- 第一个线性层,矩阵乘法的输入和输出形状为
[𝑏,𝑠,ℎ]×[ℎ,4ℎ]→[𝑏,𝑠,4ℎ]。计算量为 8𝑏𝑠h28𝑏𝑠ℎ^28bsh2 。 - 第二个线性层,矩阵乘法的输入和输出形状为
[𝑏,𝑠,4ℎ]×[4ℎ,ℎ]→[𝑏,𝑠,ℎ]。计算量为 8𝑏𝑠h28𝑏𝑠ℎ^28bsh2。
使用 KV Cache 时:
- 第一个线性层,矩阵乘法的输入和输出形状为
[𝑏, 1, ℎ]×[ℎ, 4ℎ]→[𝑏,1,4ℎ]。计算量为 8𝑏h28𝑏ℎ^28bh2 。 - 第二个线性层,矩阵乘法的输入和输出形状为
[𝑏, 1, 4ℎ]×[4ℎ, ℎ]→[𝑏,1,ℎ]。计算量为 8𝑏h28𝑏ℎ^28bh2 。
将上述self-attention块和MLP块计算量相加,得到:
- 采用kv cache时,得到每个transformer层的计算量大约为 24𝑏h2+4𝑏h(𝑘𝑣𝑙𝑒𝑛𝑔𝑡h+1)24𝑏ℎ^2+4𝑏ℎ(𝑘𝑣 _{𝑙𝑒𝑛𝑔𝑡ℎ}+1)24bh2+4bh(kvlength+1) 。
- 不采用kv cache时,得到每个transformer层的计算量大约为: 24𝑏𝑠h2+4𝑏𝑠2h24𝑏𝑠ℎ2+4𝑏𝑠2ℎ24bsh2+4bs2h 。
此外,另一个计算量的大头是logits的计算,将隐藏向量映射为词表大小。
- 采用kv cache时,矩阵乘法的输入和输出形状为
[𝑏,1,ℎ]×[ℎ,𝑉]→[𝑏,1,𝑉],计算量为 2𝑏h𝑉2𝑏ℎ𝑉2bhV 。 - 不采用kv cache时为,矩阵乘法的输入和输出形状为
[𝑏,𝑠,ℎ]×[ℎ,𝑉]→[𝑏,𝑠,𝑉],计算量为 2𝑏𝑠h𝑉2𝑏𝑠ℎ𝑉2bshV 。
KV Cache 显存占用分析
假设输入序列的长度为s ,输出序列的长度为n ,transformer层数为l,隐藏层维度 h,KV Cache 存储 kv_seq_len 个 KV value,形状为 [b, head_num, kv_seq_len, head_dim], 峰值kv_seq_len为 s+n ,以float16来保存KV cache,那么KV cache的峰值显存占用大小为 b(s+n)h_l_2*2=4blh(s+n) 。这里第一个 2 表示 K/V cache,第二个2表示float16占 2 个 bytes。
以GPT3-175B为例,对比KV cache与模型参数占用显存的大小。模型配置如下:
| 模型名 | 参数量 | 层数 | 隐藏维度 | 注意力头数 |
|---|---|---|---|---|
| GPT3 | 175B | 96 | 12288 | 96 |
GPT3 模型占用显存大小为350GB。假设批次大小b=64 ,输入序列长度s=512 ,输出序列长度n=32 ,则KV cache 峰值占用显存为 4blh(s+n) = 164,282,499,072 bytes ≈ 164 𝐺𝐵 ,大约是模型参数显存的0.5倍。
KV Cache 存在的问题以及优化措施
当将LLMs应用于无限输入流时,使用原始的 Dense Attention 会出现两个主要挑战:
- 上下文越长,那么矩阵占用的内存也会越多,不仅如此还会增加Decoder时候的延迟。
- 现有模型的长度外推能力有限,即当序列长度超出预训练期间设置的attention窗口大小时,其性能会下降。
因此,目前提出了一些优化方法,比如:使用滑动窗口的注意力机制,主要有如下几种方式。
- 一种方式是如下图 B 的窗口注意力(Window Attention):只缓存最近的 L 个 Token 的 KV。虽然推理效率很高,但一旦起始Token的键和值被驱逐,性能就会急剧下降。
- 一种方式是下图 C 的滑动窗口重计算(Sliding Window w/ Re-computation):根据每个新 Token 的 L 个最近 Token 重建 KV 状态。虽然它在长文本上表现良好,但其 O(TL2)O(TL^2)O(TL2) 的复杂性(源于上下文重新计算中的二次注意力)使其相当慢。

- 还有一种方式是StreamingLLM,在当前滑动窗口方法的基础上,重新引入了一些最初的 tokens 的KV在注意力计算中使用。StreamingLLM 中的KV缓存可以概念上分为两部分,如下图所示:(1)attention sink 是 4 个最初的 tokens,稳定了注意力计算;(2)Rolling KV Cache 保留了最近的token,这个窗口值是固定的。此外,还需要有些小改动来给attention注入位置信息,StreamingLLM就可以无缝地融入任何使用相对位置编码的自回归语言模型,如RoPE和ALiBi。

KV Cache 源码分析
class GPT2Attention(nn.Module):
def forward(
self,
hidden_states: Optional[Tuple[torch.FloatTensor]],
layer_past: Optional[Tuple[torch.Tensor]] = None,
attention_mask: Optional[torch.FloatTensor] = None,
head_mask: Optional[torch.FloatTensor] = None,
encoder_hidden_states: Optional[torch.Tensor] = None,
encoder_attention_mask: Optional[torch.FloatTensor] = None,
use_cache: Optional[bool] = False,
output_attentions: Optional[bool] = False,
) -> Tuple[Union[torch.Tensor, Tuple[torch.Tensor]], ...]:
...
# 拆分 Q、K、V
query, key, value = self.c_attn(hidden_states).split(self.split_size, dim=2)
...
# [batch, sequence_len, embeded_dim] -> [batch, heads, sequence_len, head_dim]
query = self._split_heads(query, self.num_heads, self.head_dim) # 当前token对应的query
key = self._split_heads(key, self.num_heads, self.head_dim) # 当前token对应的key
value = self._split_heads(value, self.num_heads, self.head_dim) # 当前token对应的value
##################################
# KV Cache 核心代码逻辑
if layer_past is not None:
past_key, past_value = layer_past # 从 KV Cache 去数据
key = torch.cat((past_key, key), dim=-2) # 将当前token的key与历史的K拼接
value = torch.cat((past_value, value), dim=-2) # 将当前token的value与历史的V拼接
if use_cache is True:
present = (key, value) # 将数据存到 KV Cache
else:
present = None
##################################
...
# 使用当前token的query与K和V计算注意力表示
attn_output, attn_weights = self._attn(query, key, value, attention_mask, head_mask) # 返回att输出(激活)和权重
# 合并多头注意力
# attn_output: [batch, heads, sequence_len, head_dim] -> [batch, heads, embed_dim]
attn_output = self._merge_heads(attn_output, self.num_heads, self.head_dim)
attn_output = self.c_proj(attn_output)
attn_output = self.resid_dropout(attn_output)
outputs = (attn_output, present)
if output_attentions:
outputs += (attn_weights,)
return outputs # a, present, (attentions)
class Attention(nn.Module):
def forward(
self,
hidden_states: torch.Tensor,
attention_mask: Optional[torch.Tensor] = None,
position_ids: Optional[torch.LongTensor] = None,
past_key_value: Optional[Tuple[torch.Tensor]] = None,
output_attentions: bool = False,
use_cache: bool = False,
) -> Tuple[torch.Tensor, Optional[torch.Tensor], Optional[Tuple[torch.Tensor]]]:
bsz, q_len, _ = hidden_states.size()
proj = self.W_pack(hidden_states)
proj = proj.unflatten(-1, (3, self.hidden_size)).unsqueeze(0).transpose(0, -2).squeeze(-2)
query_states = proj[0].view(bsz, q_len, self.num_heads, self.head_dim).transpose(1, 2)
key_states = proj[1].view(bsz, q_len, self.num_heads, self.head_dim).transpose(1, 2)
value_states = proj[2].view(bsz, q_len, self.num_heads, self.head_dim).transpose(1, 2)
kv_seq_len = key_states.shape[-2]
if past_key_value is not None:
kv_seq_len += past_key_value[0].shape[-2]
cos, sin = self.rotary_emb(value_states, seq_len=kv_seq_len)
query_states, key_states = apply_rotary_pos_emb(query_states, key_states, cos, sin, position_ids)
# [bsz, nh, t, hd]
if past_key_value is not None:
# 取出 KV Cache 中的值
# reuse k, v, self_attention
key_states = torch.cat([past_key_value[0], key_states], dim=2)
value_states = torch.cat([past_key_value[1], value_states], dim=2)
# 保存 KV Cache 中的值
past_key_value = (key_states, value_states) if use_cache else None
class LlamaAttention(nn.Module):
...
def forward(
self,
hidden_states: torch.Tensor,
attention_mask: Optional[torch.Tensor] = None,
position_ids: Optional[torch.LongTensor] = None,
past_key_value: Optional[Cache] = None,
output_attentions: bool = False,
use_cache: bool = False,
cache_position: Optional[torch.LongTensor] = None,
**kwargs,
) -> Tuple[torch.Tensor, Optional[torch.Tensor], Optional[Tuple[torch.Tensor]]]:
...
past_key_value = getattr(self, "past_key_value", past_key_value)
cos, sin = self.rotary_emb(value_states, position_ids)
query_states, key_states = apply_rotary_pos_emb(query_states, key_states, cos, sin)
if past_key_value is not None:
# sin and cos are specific to RoPE models; cache_position needed for the static cache
cache_kwargs = {"sin": sin, "cos": cos, "cache_position": cache_position}
# 将当前 Token 的 kv 值更新到 KV Cache,并返回新的 KV
key_states, value_states = past_key_value.update(key_states, value_states, self.layer_idx, cache_kwargs)
...
return attn_output, attn_weights, past_key_value
@dataclass
class Cache:
"""
所有Cache的基础抽象类。实际数据结构由每个子类决定。
"""
def update(
self,
key_states: torch.Tensor,
value_states: torch.Tensor,
layer_idx: int,
cache_kwargs: Optional[Dict[str, Any]] = None,
) -> Tuple[torch.Tensor, torch.Tensor]:
"""
Updates the cache with the new `key_states` and `value_states` for the layer `layer_idx`.
Parameters:
key_states (`torch.Tensor`):
The new key states to cache.
value_states (`torch.Tensor`):
The new value states to cache.
layer_idx (`int`):
The index of the layer to cache the states for.
cache_kwargs (`Dict[str, Any]`, `optional`):
Additional arguments for the cache subclass. These are specific to each subclass and allow new types of
cache to be created.
Return:
A tuple containing the updated key and value states.
"""
raise NotImplementedError("Make sure to implement `update` in a subclass.")
def get_seq_length(self, layer_idx: Optional[int] = 0) -> int:
"""Returns the sequence length of the cached states. A layer index can be optionally passed."""
raise NotImplementedError("Make sure to implement `get_seq_length` in a subclass.")
def get_max_length(self) -> Optional[int]:
"""Returns the maximum sequence length of the cached states, if there is any."""
raise NotImplementedError("Make sure to implement `get_max_length` in a subclass.")
def get_usable_length(self, new_seq_length: int, layer_idx: Optional[int] = 0) -> int:
"""Given the sequence length of the new inputs, returns the usable length of the cache."""
# Cache without size limit -> all cache is usable
# Cache with size limit -> if the length cache plus the length of the new inputs is larger the maximum cache
# length, we will need to evict part of the cache (and thus not all cache is usable)
max_length = self.get_max_length()
previous_seq_length = self.get_seq_length(layer_idx)
if max_length is not None and previous_seq_length + new_seq_length > max_length:
return max_length - new_seq_length
return previous_seq_length
@property
def seen_tokens(self):
logger.warning_once(
"The `seen_tokens` attribute is deprecated and will be removed in v4.41. Use the `cache_position` "
"model input instead."
)
if hasattr(self, "_seen_tokens"):
return self._seen_tokens
else:
return None
class DynamicCache(Cache):
# 随着生成更多 Token 而动态增长的Cache。这是生成模型的默认设置。
# 它将键和值状态存储为张量列表,每层一个张量。每个张量的期望形状是
# [batch_size, num_heads, seq_len, head_dim]。
def update(
self,
key_states: torch.Tensor,
value_states: torch.Tensor,
layer_idx: int,
cache_kwargs: Optional[Dict[str, Any]] = None,
) -> Tuple[torch.Tensor, torch.Tensor]:
# Update the number of seen tokens
if layer_idx == 0:
self._seen_tokens += key_states.shape[-2]
# Update the cache
if len(self.key_cache) <= layer_idx:
self.key_cache.append(key_states)
self.value_cache.append(value_states)
else:
self.key_cache[layer_idx] = torch.cat([self.key_cache[layer_idx], key_states], dim=-2)
self.value_cache[layer_idx] = torch.cat([self.value_cache[layer_idx], value_states], dim=-2)
return self.key_cache[layer_idx], self.value_cache[layer_idx]
class StaticCache(Cache):
"""
与 torch.compile(model) 一起使用的静态 Cache 类
"""
...
def update(
self,
key_states: torch.Tensor,
value_states: torch.Tensor,
layer_idx: int,
cache_kwargs: Optional[Dict[str, Any]] = None,
) -> Tuple[torch.Tensor, torch.Tensor]:
"""
Updates the cache with the new `key_states` and `value_states` for the layer `layer_idx`.
使用张量进行索引是非常重要的,否则你会向设备引入一个副本。
Parameters:
key_states (`torch.Tensor`):
The new key states to cache.
value_states (`torch.Tensor`):
The new value states to cache.
layer_idx (`int`):
The index of the layer to cache the states for. Kept for backward compatibility
cache_kwargs (`Dict[str, Any]`, `optional`):
Additional arguments for the cache subclass. The `StaticCache` just needs the `q_len`
to know how much of the cache it should overwrite.
Return:
A tuple containing the updated key and value states.
"""
new_cache_positions = cache_kwargs.get("cache_position")
k_out = self.key_cache
v_out = self.value_cache
k_out[:, :, new_cache_positions] = key_states
v_out[:, :, new_cache_positions] = value_states
return k_out, v_out
class SinkCache(Cache):
"""
# 正如[Attention Sinks 论文](https://arxiv.org/abs/2309.17453)中所描述的缓存。
# 它允许模型生成超出其上下文窗口的长度,而不会失去会话的流畅性。
# 因为它抛弃了过去tokens,模型将失去生成依赖于被丢弃的上下文的tokens的能力。
# 它将键和值状态存储为张量列表,每层一个张量。每个张量的期望形状是
# [batch_size, num_heads, seq_len, head_dim]
"""
...
def update(
self,
key_states: torch.Tensor,
value_states: torch.Tensor,
layer_idx: int,
cache_kwargs: Optional[Dict[str, Any]] = None,
) -> Tuple[torch.Tensor, torch.Tensor]:
# Optional kwargs for `SinkCache` -- needed on models using RoPE. `partial_rotation_size` is used on models
# with partially rotated position embeddings, like Phi or Persimmon.
sin = cache_kwargs.get("sin")
cos = cache_kwargs.get("cos")
partial_rotation_size = cache_kwargs.get("partial_rotation_size")
using_rope = cos is not None and sin is not None
# Update the number of seen tokens
if layer_idx == 0:
self._seen_tokens += key_states.shape[-2]
# [bsz, num_heads, seq_len, head_dim]
if len(self.key_cache) <= layer_idx:
# Empty cache
self.key_cache.append(key_states)
self.value_cache.append(value_states)
elif key_states.shape[-2] + self.get_seq_length(layer_idx) < self.window_length:
# Growing cache
self.key_cache[layer_idx] = torch.cat([self.key_cache[layer_idx], key_states], dim=-2)
self.value_cache[layer_idx] = torch.cat([self.value_cache[layer_idx], value_states], dim=-2)
else:
# Shifting cache
keys_to_keep = self.key_cache[layer_idx][
:, :, -self.window_length + self.num_sink_tokens + key_states.shape[-2] :
]
# On RoPE models, we need to recompute the Key rotation as the tokens are shifted
if using_rope:
rerotation_cos, rerotation_sin = self._get_rerotation_cos_sin(
key_states, cos[: self.window_length], sin[: self.window_length]
)
if partial_rotation_size is not None:
keys_to_keep, keys_pass = (
keys_to_keep[..., :partial_rotation_size],
keys_to_keep[..., partial_rotation_size:],
)
keys_to_keep = self._apply_key_rotary_pos_emb(keys_to_keep, rerotation_cos, rerotation_sin)
if partial_rotation_size is not None:
keys_to_keep = torch.cat((keys_to_keep, keys_pass), dim=-1)
# Concatenate sink tokens, shifted & rotated tokens (if needed), and new tokens
sink_keys = self.key_cache[layer_idx][:, :, : self.num_sink_tokens]
self.key_cache[layer_idx] = torch.cat([sink_keys, keys_to_keep, key_states], dim=-2)
sink_values = self.value_cache[layer_idx][:, :, : self.num_sink_tokens]
values_to_keep = self.value_cache[layer_idx][
:, :, -self.window_length + self.num_sink_tokens + value_states.shape[-2] :
]
self.value_cache[layer_idx] = torch.cat([sink_values, values_to_keep, value_states], dim=-2)
return self.key_cache[layer_idx], self.value_cache[layer_idx]
从 GPT2 、 Baichuan2 和 LLaMA 的源码中可以看到 KV Cache 核心代码的实现就几行并不复杂,但是带来的收益却挺大。
结语
本文简要分析了 KV Cache 原理、源码以及计算量和显存占用,这是一种典型的通过空间换时间(计算)的技术,虽然并不复杂,但是现在基本上是仅编码器Transformer架构生成大语言模型必备优化技术。
如何系统的去学习大模型LLM ?
作为一名热心肠的互联网老兵,我意识到有很多经验和知识值得分享给大家,也可以通过我们的能力和经验解答大家在人工智能学习中的很多困惑,所以在工作繁忙的情况下还是坚持各种整理和分享。
但苦于知识传播途径有限,很多互联网行业朋友无法获得正确的资料得到学习提升,故此将并将重要的 AI大模型资料 包括AI大模型入门学习思维导图、精品AI大模型学习书籍手册、视频教程、实战学习等录播视频免费分享出来。
😝有需要的小伙伴,可以V扫描下方二维码免费领取🆓

一、全套AGI大模型学习路线
AI大模型时代的学习之旅:从基础到前沿,掌握人工智能的核心技能!

二、640套AI大模型报告合集
这套包含640份报告的合集,涵盖了AI大模型的理论研究、技术实现、行业应用等多个方面。无论您是科研人员、工程师,还是对AI大模型感兴趣的爱好者,这套报告合集都将为您提供宝贵的信息和启示。

三、AI大模型经典PDF籍
随着人工智能技术的飞速发展,AI大模型已经成为了当今科技领域的一大热点。这些大型预训练模型,如GPT-3、BERT、XLNet等,以其强大的语言理解和生成能力,正在改变我们对人工智能的认识。 那以下这些PDF籍就是非常不错的学习资源。

四、AI大模型商业化落地方案

阶段1:AI大模型时代的基础理解
- 目标:了解AI大模型的基本概念、发展历程和核心原理。
- 内容:
- L1.1 人工智能简述与大模型起源
- L1.2 大模型与通用人工智能
- L1.3 GPT模型的发展历程
- L1.4 模型工程
- L1.4.1 知识大模型
- L1.4.2 生产大模型
- L1.4.3 模型工程方法论
- L1.4.4 模型工程实践
- L1.5 GPT应用案例
阶段2:AI大模型API应用开发工程
- 目标:掌握AI大模型API的使用和开发,以及相关的编程技能。
- 内容:
- L2.1 API接口
- L2.1.1 OpenAI API接口
- L2.1.2 Python接口接入
- L2.1.3 BOT工具类框架
- L2.1.4 代码示例
- L2.2 Prompt框架
- L2.2.1 什么是Prompt
- L2.2.2 Prompt框架应用现状
- L2.2.3 基于GPTAS的Prompt框架
- L2.2.4 Prompt框架与Thought
- L2.2.5 Prompt框架与提示词
- L2.3 流水线工程
- L2.3.1 流水线工程的概念
- L2.3.2 流水线工程的优点
- L2.3.3 流水线工程的应用
- L2.4 总结与展望
阶段3:AI大模型应用架构实践
- 目标:深入理解AI大模型的应用架构,并能够进行私有化部署。
- 内容:
- L3.1 Agent模型框架
- L3.1.1 Agent模型框架的设计理念
- L3.1.2 Agent模型框架的核心组件
- L3.1.3 Agent模型框架的实现细节
- L3.2 MetaGPT
- L3.2.1 MetaGPT的基本概念
- L3.2.2 MetaGPT的工作原理
- L3.2.3 MetaGPT的应用场景
- L3.3 ChatGLM
- L3.3.1 ChatGLM的特点
- L3.3.2 ChatGLM的开发环境
- L3.3.3 ChatGLM的使用示例
- L3.4 LLAMA
- L3.4.1 LLAMA的特点
- L3.4.2 LLAMA的开发环境
- L3.4.3 LLAMA的使用示例
- L3.5 其他大模型介绍
阶段4:AI大模型私有化部署
- 目标:掌握多种AI大模型的私有化部署,包括多模态和特定领域模型。
- 内容:
- L4.1 模型私有化部署概述
- L4.2 模型私有化部署的关键技术
- L4.3 模型私有化部署的实施步骤
- L4.4 模型私有化部署的应用场景
学习计划:
- 阶段1:1-2个月,建立AI大模型的基础知识体系。
- 阶段2:2-3个月,专注于API应用开发能力的提升。
- 阶段3:3-4个月,深入实践AI大模型的应用架构和私有化部署。
- 阶段4:4-5个月,专注于高级模型的应用和部署。
这份完整版的大模型 LLM 学习资料已经上传CSDN,朋友们如果需要可以微信扫描下方CSDN官方认证二维码免费领取【保证100%免费】
😝有需要的小伙伴,可以Vx扫描下方二维码免费领取🆓


开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献13条内容
已为社区贡献13条内容





所有评论(0)