数据结构 | 二叉树先根、中根、后根遍历的非递归算法

二叉树先根遍历、中根遍历、后根遍历非递归算法的C++代码

易水卷长空

8825人浏览 · 2022-01-29 23:56:05

易水卷长空 · 2022-01-29 23:56:05 发布

上期文章：数据结构 | 树与二叉树

参考教材：《数据结构》，刘大有

编程语言： C++

（一）二叉树的存储结构

二叉树在计算机中具有顺序存储和链式存储两种存储方式。在本文所讨论的算法中，二叉树均是采用二叉链表的存储方式

struct Node{
    Node *left;
    Node *right;
    char data;
    Node():left(nullptr),right(nullptr),data('#'){}
};

其中left为指向该结点左儿子的指针，right为指向该结点右儿子的指针

（二）二叉树的遍历

先根遍历非递归算法

先根遍历的顺序为①访问根、②遍历左子树、③遍历右子树

为了实现先根遍历的非递归算法，我们需要引进一个辅助堆栈，栈的元素为Node *类型

//栈
class Stack{
public:
    Stack():top(0){
        for(int i=0;i<s_size;i++){
            s[i]=nullptr;
        }
    }
    //入栈
    void push(Node *p){
        if(top<s_size){
            s[top]=p;
            top++;
        }else{
            cout<<"Stack overflow!"<<endl;
            return;
        }
    }
    //出栈
    Node *pop(){
        if(top==0){
            return nullptr;
        }else{
            top--;
            return s[top];
        }
    }
    bool isEmpty(){
        if(top==0)
            return true;
        else
            return false;
    }
private:
    const int s_size=20;
    Node *s[s_size];
    int top;
};

先根遍历的非递归算法较为简单，用自然语言描述就是：

根结点入栈
判断，如果栈为空则结束算法；否则，当栈不为空时：弹栈，访问该结点；如果该结点右儿子存在则入栈；如果该结点左儿子存在则入栈
返回第2步

/*先根遍历非递归算法*/
void nPreOrder(Node * root){
    if(root == nullptr){
        return;
    }
    Stack s;
    Node *p=root;
    //根节点入栈
    s.push(p);
    //栈不为空时:
    while(!s.isEmpty()){
        //弹栈:
        p=s.pop();
        cout<<p->data;
        //右儿子入栈:
        if(p->right!=nullptr){
            s.push(p->right);
        }
        //左儿子入栈:
        if(p->left!=nullptr){
            s.push(p->left);
        }
    }
    return;
}

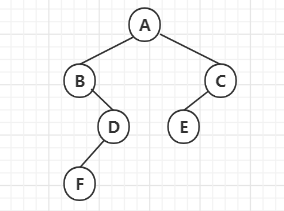
以下面这棵树为例

算法执行过程中，栈的变化情况如下，最终输出的先根序列为ABDFCE：

中根遍历非递归算法

中根遍历的顺序为①遍历左子树、②访问根、③遍历右子树

中根遍历的非递归算法也需要引入辅助堆栈，栈的结构与上面先根遍历非递归算法用到的栈Stack相同

中根遍历非递归算法思想：

令p=root
判断，如果栈不为空或p不等于nullptr，执行下一步；否则算法结束
当p不等于nullptr（空指针）时，让p结点入栈；如果p结点的左儿子存在，也让其左儿子入栈；如果p结点左儿子的左儿子存在，依然让其左儿子的左儿子入栈......以此类推，直到p的某一个后裔结点不存在左儿子时，执行下一步
弹出栈顶元素（这时候栈一定不为空），访问该结点，把该结点的右儿子的地址赋值给p；返回第2步

/*中根遍历非递归算法*/
void nInOrder(Node * root){
    if(root==nullptr){
        return;
    }
    Stack s;
    Node *p=root;

    while( (!s.isEmpty()) || (p!=nullptr) ){
        while(p!=nullptr){
            s.push(p);
            p=p->left;
        }
        p=s.pop();
        cout<<p->data;
        p=p->right;
    }
}

以下面这棵树为例

算法执行过程中，栈的变化情况如下，最终输出的中根序列为BFDAEC：

后根遍历非递归算法

后根遍历的顺序为①遍历左子树、②遍历右子树、③访问根

后根遍历的非递归算法依然需要引入辅助堆栈。但是注意，这里栈的结构与上面的栈结构不同，这里栈的元素为包含Node *和int 类型的结构体

//栈2元素的结构
struct NodeOfStack{
    Node *pnode;
    int times;//入栈次数
    NodeOfStack():pnode(nullptr),times(0){}
};

其中pnode为Node *类型的指针，times记录了该结点入栈的次数，times的值可取0,1,2

栈2的定义如下：

//栈2
class Stack2{
public:
    Stack2():top(0){
        for(int i=0;i<s_size;i++){
            s[i].pnode=nullptr;
            s[i].times=0;
        }
    }
    //入栈
    void push(Node *p,int t){
        if(top<s_size){
            s[top].pnode=p;
            s[top].times=t;
            top++;
        }else{
            cout<<"Stack overflow!"<<endl;
            return;
        }
    }
    //出栈
    NodeOfStack pop(){
        if(top>0){
            top--;
            return s[top];
        }
    }
    bool isEmpty(){
        if(top==0)
            return true;
        else
            return false;
    }
private:
    const int s_size=20;
    NodeOfStack s[20];
    int top;
};

后根遍历的非递归算法：

(root,0)入栈
判断，如果栈为空，结束算法；否则，栈不为空时：弹栈，记为(p,times)。①若times==0，(p,1)入栈，如果p的左儿子存在则(p->left,0)也压入栈。②若times==1，(p,2)入栈，如果p的右儿子存在则(p->right,0)也压入栈。③若times==2，访问p结点
返回第2步


/*后根遍历非递归算法*/
void nPostOrder(Node * root){
    if(root==nullptr){
        return;
    }
    Stack2 s;
    s.push(root,0);
    while(!s.isEmpty()){
        NodeOfStack nos=s.pop();//中间变量，存储每一次栈弹出的数据
        Node *p=nos.pnode;
        if(nos.times==0){
            s.push(nos.pnode,1);
            if(p->left!=nullptr){
                s.push(p->left,0);
            }
        }else if(nos.times==1){
            s.push(nos.pnode,2);
            if(p->right!=nullptr){
                s.push(p->right,0);
            }
        }else if(nos.times==2){
            cout<<p->data;
        }
    }
}