随机过程(2.2)—— 多维高斯分布
多维高斯分布是一种特殊的多维随机分布,应用非常广泛本文介绍多维高斯分布的定义、几何理解和部分基本性质
- 随机过程(2.1)—— 多维随机变量(随机向量)
- 多维高斯分布是一种特殊的多维随机分布,应用非常广泛。本文参考【机器学习】【白板推导系列】
1. 定义
- 若
n
n
n 维 r.v.
X
\pmb{X}
X 的概率密度函数为
f ( x ) = f ( x 1 , . . . , x n ) = 1 ( 2 π ) n / 2 ∣ B ∣ 1 / 2 e − 1 2 ( x − a ) ⊤ B − 1 ( x − a ) f(\pmb{x}) = f(x_1,...,x_n) = \frac{1}{(2\pi)^{n/2}|B|^{1/2}}e^{-\frac{1}{2}(\mathbf{x}-\mathbf{a})^\top \mathbf{B}^{-1}(\mathbf{x}-\mathbf{a})} f(x)=f(x1,...,xn)=(2π)n/2∣B∣1/21e−21(x−a)⊤B−1(x−a) 其中 B \pmb{B} B 为 n n n 阶实对称正定矩阵(所有特征值 > 0),则称随机向量 X \pmb{X} X 服从期望为 a \pmb{a} a,协方差矩阵为 B \pmb{B} B 的多维正态分布,记为 X ∼ N ( a , B ) \pmb{X}\sim N(\pmb{a},\pmb{B}) X∼N(a,B) - 注意这里
B
\pmb{B}
B 是一个协方差矩阵,展开为
B = [ D X 1 Cov ( X 1 , X 2 ) … Cov ( X 1 , X n ) Cov ( X 2 , X 1 ) D X 2 … Cov ( X 2 , X n ) ⋮ ⋮ ⋮ Cov ( X n , X 1 ) Cov ( X n , X 2 ) … D X n ] = [ σ 1 2 ρ 12 σ 1 σ 2 … ρ 1 n σ 1 σ n ρ 21 σ 2 σ 1 σ 2 2 … ρ 2 n σ 2 σ n ⋮ ⋮ ⋮ ρ n , 1 σ n σ 1 ρ n , 2 σ n σ 2 … σ n 2 ] \begin{aligned} \pmb{B} &= \begin{bmatrix} DX_1 &\text{Cov}(X_1,X_2) &\dots &\text{Cov}(X_1,X_n) \\ \text{Cov}(X_2,X_1) &DX_2 &\dots &\text{Cov}(X_2,X_n) \\ \vdots &\vdots &&\vdots\\ \text{Cov}(X_n,X_1) &\text{Cov}(X_n,X_2) &\dots &DX_n \end{bmatrix}\\ & = \begin{bmatrix} \sigma_1^2 &\rho_{12}\sigma_1\sigma_2 &\dots &\rho_{1n}\sigma_1\sigma_n \\ \rho_{21}\sigma_2\sigma_1 &\sigma_2^2 &\dots &\rho_{2n}\sigma_2\sigma_n \\ \vdots &\vdots &&\vdots\\ \rho_{n,1}\sigma_n\sigma_1 &\rho_{n,2}\sigma_n\sigma_2 &\dots &\sigma_n^2 \end{bmatrix} \end{aligned} B= DX1Cov(X2,X1)⋮Cov(Xn,X1)Cov(X1,X2)DX2⋮Cov(Xn,X2)………Cov(X1,Xn)Cov(X2,Xn)⋮DXn = σ12ρ21σ2σ1⋮ρn,1σnσ1ρ12σ1σ2σ22⋮ρn,2σnσ2………ρ1nσ1σnρ2nσ2σn⋮σn2 显然它 B \pmb{B} B 是实对称矩阵,通常情况下(只要 X i X_i Xi 不为常数)其任意阶顺序主子式 > 0,故正定。这种实对称正定矩阵是一种正定 hermitian 矩阵,可以做乔里斯基分解 B = L L ⊤ \pmb{B} = \pmb{LL^\top} B=LL⊤( L \pmb{L} L 是某下三角矩阵),这是处理多维高斯分布问题的常用技巧之一 - 显然
f
(
x
)
f(\pmb{x})
f(x) 在任意取值下都是非负的,下面证明
∫
R
n
f
(
x
)
d
x
=
1
\int_{R^n} f(\pmb{x})d\pmb{x}=1
∫Rnf(x)dx=1 以说明它是一个合法的概率密度函数,这个证明中用到两个技巧
- 上面提到的 B = L L ⊤ \pmb{B} = \pmb{LL^\top} B=LL⊤
- 向量对向量求导会得到一个 Jacobi 行列式,令
x
=
L
y
+
a
\pmb{x} = \pmb{Ly}+\pmb{a}
x=Ly+a,则
∂
x
∂
y
=
∣
L
∣
\frac{\partial\mathbf{x}}{\partial\mathbf{y}} = |\pmb{L}|
∂y∂x=∣L∣

2. 理解
2.1 几何意义
-
X
∼
N
(
a
,
B
)
\pmb{X}\sim N(\pmb{a},\pmb{B})
X∼N(a,B) 的概率密度函数
f
(
x
)
=
1
(
2
π
)
n
/
2
∣
B
∣
1
/
2
e
−
1
2
(
x
−
a
)
⊤
B
−
1
(
x
−
a
)
f(\pmb{x}) = \frac{1}{(2\pi)^{n/2}|B|^{1/2}}e^{-\frac{1}{2}(\mathbf{x}-\mathbf{a})^\top \mathbf{B}^{-1}(\mathbf{x}-\mathbf{a})}
f(x)=(2π)n/2∣B∣1/21e−21(x−a)⊤B−1(x−a),关注其中的指数部分,这是一个二次型,设为
△
=
(
x
−
a
)
⊤
B
−
1
(
x
−
a
)
\triangle = (\mathbf{x}-\mathbf{a})^\top \mathbf{B}^{-1}(\mathbf{x}-\mathbf{a})
△=(x−a)⊤B−1(x−a)
-
首先明确 ( x − a ) (\mathbf{x-a}) (x−a) 尺寸为 n × 1 n\times 1 n×1, B \mathbf{B} B 尺寸为 n × n n\times n n×n, △ \triangle △ 是一个数,可以看作 x \mathbf{x} x 和 a \mathbf{a} a 间的马氏距离
-
注意 B \pmb{B} B 是实对称矩阵,一般情况下( X i X_i Xi 不为常数)认为它是正定矩阵,其具有以下性质
- 正定对称
⇒
\Rightarrow
⇒
乔里斯基分解: B = L L ⊤ \pmb{B} = \pmb{LL^\top} B=LL⊤,其中 L \pmb{L} L 是下三角矩阵 - 正定对称
⇒
\Rightarrow
⇒
LDL分解: B = L D L ⊤ \pmb{B} = \pmb{LDL^\top} B=LDL⊤,其中 D \pmb{D} D 是一个对角阵, L \pmb{L} L 是主对角线全为 1 的下三角矩阵 - 实对称
⇒
\Rightarrow
⇒
B
n
×
n
\pmb{B}_{n\times n}
Bn×n
正交相似于其特征值组成的对角阵,即 B = U Λ U ⊤ \pmb{B = U\Lambda U^\top} B=UΛU⊤,其中 U \pmb{U} U 是正交矩阵(有 U U ⊤ = U ⊤ U = E \pmb{UU^\top}=\pmb{U^\top U} = \pmb{E} UU⊤=U⊤U=E),其列向量为 B \pmb{B} B 的特征向量, Λ = diag { λ 1 , λ 2 , . . . , λ p } \Lambda = \text{diag} \{\lambda_1,\lambda_2,...,\lambda_p\} Λ=diag{λ1,λ2,...,λp}( λ i \lambda_i λi 是 B \pmb{B} B 的特征值)。这是因为 n n n 阶实对称矩阵的所有特征值都是实数,各个特征值的代数重数和几何重数相等(有 n n n 个线性无关特征向量),且所有特征向量相互正交(参考此处)。此结论也可理解为 Schur 定理在实数域上的推论 - 可相似对角化
⇒
\Rightarrow
⇒
B
n
×
n
\pmb{B}_{n\times n}
Bn×n 可以
谱分解: B = P Λ P − 1 \pmb{B = P\Lambda P^{-1}} B=PΛP−1,其中 P \pmb{P} P 的列向量是 B \pmb{B} B 的(右)特征向量, P − 1 \pmb{P}^{-1} P−1 的行向量是 B \pmb{B} B 的左特征向量(参考此处), Λ = diag { λ 1 , λ 2 , . . . , λ p } \Lambda = \text{diag} \{\lambda_1,\lambda_2,...,\lambda_p\} Λ=diag{λ1,λ2,...,λp}( λ i \lambda_i λi 是 B \pmb{B} B 的特征值)。注意性质 3 中的 U \pmb{U} U 是正交矩阵,有 U − 1 = U ⊤ \pmb{U^{-1}=U^\top} U−1=U⊤,因此实对称矩阵 B \pmb{B} B 的谱分解和 3 中的相似对角化是一样的
利用上述性质 3/4 分析 B − 1 \pmb{B}^{-1} B−1,可如下展开(其中 u i \pmb{u_i} ui 是列向量,尺寸 n × 1 n\times 1 n×1)
B − 1 = ( U Λ U ⊤ ) − 1 = ( U ⊤ ) − 1 Λ − 1 U − 1 = U Λ − 1 U ⊤ = ∑ i = 1 n u i 1 λ i u i ⊤ \begin{aligned} \pmb{B}^{-1} &= (\pmb{U\Lambda U^\top})^{-1} \\ &= (\pmb{U^\top})^{-1} \pmb{\Lambda}^{-1}\pmb{U}^{-1} \\ &= \pmb{U}\pmb{\Lambda}^{-1}\pmb{U^\top} \\ &=\sum_{i=1}^n \pmb{u_i}\frac{1}{\lambda_i}\pmb{u_i^\top} \end{aligned} B−1=(UΛU⊤)−1=(U⊤)−1Λ−1U−1=UΛ−1U⊤=i=1∑nuiλi1ui⊤ - 正定对称
⇒
\Rightarrow
⇒
-
- 进一步考虑多元高斯分布指数部分的二次型
△ = ( x − a ) ⊤ B − 1 ( x − a ) = ( x − a ) ⊤ ∑ i = 1 n u i 1 λ i u i ⊤ ( x − a ) = ∑ i = 1 n ( x − a ) ⊤ u i 1 λ i u i ⊤ ( x − a ) = 设 y i = ( x − a ) ⊤ u i ∑ i = 1 n y i 2 λ i \begin{aligned} \triangle &= (\mathbf{x}-\mathbf{a})^\top \mathbf{B}^{-1}(\mathbf{x}-\mathbf{a}) \\ &= (\mathbf{x}-\mathbf{a})^\top \sum_{i=1}^n \pmb{u_i}\frac{1}{\lambda_i}\pmb{u_i^\top} (\mathbf{x}-\mathbf{a}) \\ &= \sum_{i=1}^n (\mathbf{x}-\mathbf{a})^\top \pmb{u_i}\frac{1}{\lambda_i}\pmb{u_i^\top} (\mathbf{x}-\mathbf{a}) \\ &\xlongequal{\quad设\mathbf{y_i}= (\mathbf{x}-\mathbf{a})^\top \mathbf{u_i}\quad} \sum_{i=1}^n \frac{y_i^2}{\lambda_i} \end{aligned} △=(x−a)⊤B−1(x−a)=(x−a)⊤i=1∑nuiλi1ui⊤(x−a)=i=1∑n(x−a)⊤uiλi1ui⊤(x−a)设yi=(x−a)⊤uii=1∑nλiyi2 可见 △ = k \triangle=k △=k 时, △ = ∑ i = 1 n y i 2 λ i = k \triangle=\sum_{i=1}^n \frac{y_i^2}{\lambda_i} = k △=∑i=1nλiyi2=k 是 p p p 维空间中一个超椭圆。注意到 y i = ( x − a ) ⊤ u i y_i= (\pmb{x}-\pmb{a})^\top \pmb{u_i} yi=(x−a)⊤ui,可以看作先把 x \pmb{x} x 沿 a \pmb{a} a 方向平移,然后向 u i \pmb{u_i} ui 方向上的投影。不妨在 u i \pmb{u_i} ui 方向设置坐标轴 y i \pmb{y_i} yi,二维情况( n = 2 n=2 n=2)的示意图如下

可见随着 k k k 值变化, △ \triangle △ 对应到空间中一系列超椭圆,若把 k k k 看做等高线高度,这一系列椭圆就形成了一个柱状体。进一步考虑整个 n 元高斯分布的概率密度函数 f ( x ) = 1 ( 2 π ) n / 2 ∣ B ∣ 1 / 2 e − 1 2 △ f(\pmb{x}) = \frac{1}{(2\pi)^{n/2}|B|^{1/2}}e^{-\frac{1}{2}\triangle} f(x)=(2π)n/2∣B∣1/21e−21△,前面分数部分是个常数, e x e^x ex 则是和 x x x 正相关,所以概率密度函数 f ( x ) f(\pmb{x}) f(x) 也是一个相似的柱状体 - 可以如下绘制二维情况下
f
(
x
)
f(\pmb{x})
f(x) 图像,这里设置期望为
a
=
[
0
0
]
\pmb{a} = \begin{bmatrix}0\\0 \end{bmatrix}
a=[00],协方差矩阵为
B
=
[
0.8
0.2
0.2
0.2
]
\pmb{B} = \begin{bmatrix}0.8 &0.2\\0.2 &0.2 \end{bmatrix}
B=[0.80.20.20.2]
%matplotlib notebook import numpy as np import scipy.stats as st import matplotlib.pylab as plt from mpl_toolkits.mplot3d import Axes3D mu = np.array([0,0]) cov = np.array([[0.8, 0.2], [0.2, 0.2]]) fig = plt.figure(figsize = (10,5)) a0 = fig.add_subplot(1,2,1,label='a0',projection='3d') a1 = fig.add_subplot(1,2,2,label='a1',projection='3d') x, y = np.mgrid[-2.5:2.5:.1, -2.5:2.5:.1] pos = np.empty(x.shape + (2,)) pos[:, :, 0] = x; pos[:, :, 1] = y rv = st.multivariate_normal(mu, cov) # 生成多元正态分布 a0.scatter(x, y, rv.pdf(pos),s=1,alpha=0.5,cmap="rainbow") a1.plot_surface(x, y, rv.pdf(pos),alpha=0.5,cmap=plt.cm.cool)


2.2 参数数量
- 考察上述
B
\pmb{B}
B 矩阵的参数个数,由于
B
\pmb{B}
B 是对称矩阵,当尺寸为
n
×
n
n\times n
n×n 时,参数有
1
+
2
+
.
.
.
+
n
=
n
2
+
n
2
1+2+...+n = \frac{n^2+n}{2}
1+2+...+n=2n2+n 个,这时所有参数都非零,意味着
n
n
n 元高斯随机变量
x
=
[
x
1
x
2
⋮
x
n
]
\pmb{x}=\begin{bmatrix}x_1\\x_2\\\vdots\\x_n \end{bmatrix}
x=
x1x2⋮xn
中任意两个维度
x
i
,
x
j
,
i
≠
j
x_i,x_j,i\neq j
xi,xj,i=j 相关。举例来说,期望为
a
=
[
1
2
]
\pmb{a} = \begin{bmatrix}1\\2 \end{bmatrix}
a=[12],协方差矩阵为
B
=
[
0.8
0.2
0.2
0.2
]
\pmb{B} = \begin{bmatrix}0.8 &0.2\\0.2 &0.2 \end{bmatrix}
B=[0.80.20.20.2] 时属于这种情况,此时
△
\triangle
△ 对应的超椭圆是倾斜的,如下所示
%matplotlib notebook import numpy as np import scipy.stats as st import matplotlib.pylab as plt from mpl_toolkits.mplot3d import Axes3D mu = np.array([1,2]) cov = np.array([[0.8, 0.2], [0.2, 0.2]]) fig = plt.figure(figsize = (10,5)) a0 = fig.add_subplot(1,2,1,label='a0',projection='3d') a1 = fig.add_subplot(1,2,2,label='a1') x, y = np.mgrid[-1.5:3.5:.1, -0.5:4.5:.1] pos = np.empty(x.shape + (2,)) pos[:, :, 0] = x; pos[:, :, 1] = y rv = st.multivariate_normal(mu, cov) # 生成多元正态分布 a0.scatter(x, y, rv.pdf(pos),s=1,alpha=0.5,cmap="rainbow") a1.contourf(x, y, rv.pdf(pos)) # 等高线 a1.grid(alpha=0.5) # 坐标网格

- 希望减少参数数量,可以假设 n n n 元高斯随机变量 x = [ x 1 x 2 ⋮ x n ] \pmb{x}=\begin{bmatrix}x_1\\x_2\\\vdots\\x_n \end{bmatrix} x= x1x2⋮xn 中任意两个维度 x i , x j , i ≠ j x_i,x_j,i\neq j xi,xj,i=j 相互独立,这时 B \pmb{B} B 除了主对角元素外其他元素都是 0 0 0,参数减少到 n n n 个。举例来说,期望为 a = [ 1 2 ] \pmb{a} = \begin{bmatrix}1\\2 \end{bmatrix} a=[12],协方差矩阵为 B = [ 0.8 0 0 0.2 ] \pmb{B} = \begin{bmatrix}0.8 &0\\0 &0.2 \end{bmatrix} B=[0.8000.2] 时属于这种情况,此时 △ \triangle △ 对应的超椭圆是正的,如下所示

- 进一步减少参数数量,可以假设 n n n 元高斯随机变量 x = [ x 1 x 2 ⋮ x n ] \pmb{x}=\begin{bmatrix}x_1\\x_2\\\vdots\\x_n \end{bmatrix} x= x1x2⋮xn 中任意两个维度 x i , x j , i ≠ j x_i,x_j,i\neq j xi,xj,i=j 相互独立且各向同性,这时 B \pmb{B} B 除了主对角元素外其他元素都是 0 0 0,且主对角线元素都为相等正数,参数减少到 1 1 1 个。举例来说,期望为 a = [ 1 2 ] \pmb{a} = \begin{bmatrix}1\\2 \end{bmatrix} a=[12],协方差矩阵为 B = [ 1 0 0 1 ] \pmb{B} = \begin{bmatrix}1 &0\\0 &1 \end{bmatrix} B=[1001] 时属于这种情况,此时 △ \triangle △ 对应的超椭圆变为正圆,如下所示

- 可以使用极大似然估计来估计多维高斯分布的参数,请参考:一文看懂 “极大似然估计” 与 “最大后验估计” —— 极大似然估计篇
3. 特征函数
- 注意到 n n n 元正态分布函数的概率密度函数很复杂,要计算 B \pmb{B} B 的逆和行列式,所以我们一般通过特征函数来研究其性质
- 普通一元正态分布
X
∼
N
(
μ
,
σ
2
)
X \sim N(\mu,\sigma^2)
X∼N(μ,σ2) 的特征函数为(证明见
4.2节分量独立性证明)
φ X ( t ) = e i t μ − 1 2 t 2 σ 2 \varphi_X(t) = e^{it\mu-\frac{1}{2}t^2\sigma^2} φX(t)=eitμ−21t2σ2 -
n
n
n 元正态分布
X
∼
N
(
a
,
B
)
\pmb{X}\sim N(\pmb{a},\pmb{B})
X∼N(a,B) 的特征函数为
φ x ( t ) = e i t ⊤ a − 1 2 t ⊤ B t \varphi_{\mathbf{x}}(\mathbf{t}) = e^{i\mathbf{t^\top a}-\frac{1}{2}\mathbf{t^\top Bt}} φx(t)=eit⊤a−21t⊤Bt 详细证明过程如下

4. 性质
4.1 边缘分布
“多元正态随机向量” 的每个元素是 “一个正态随机变量”: X j ∼ N ( a j , b j j ) X_j \sim N(a_j,b_{jj}) Xj∼N(aj,bjj)“多元正态随机向量” 的部分向量仍为 “多元正态随机向量”:若 X ∼ N ( a , B ) \pmb{X} \sim N(\pmb{a,B}) X∼N(a,B),则其第 k 1 , . . . , k m k_1,...,k_m k1,...,km 分量组成的随机向量满足
X ∗ = [ X k 1 X k 2 ⋮ X k m ] ∼ N ( a ∗ , B ∗ ) \pmb{X}^* = \begin{bmatrix}X_{k1}\\X_{k2}\\\vdots \\X_{km} \end{bmatrix} \sim N(\pmb{a}^*,\pmb{B}^*) X∗= Xk1Xk2⋮Xkm ∼N(a∗,B∗) 其中 B ∗ = [ I m 0 ] B [ I m 0 ] \pmb{B}^* = \begin{bmatrix}\pmb{I}_m &\pmb{0}\end{bmatrix}\pmb{B}\begin{bmatrix}\pmb{I}_m \\\pmb{0}\end{bmatrix} B∗=[Im0]B[Im0] 是保留 B \pmb{B} B 的第 k 1 , . . . , k m k_1,...,k_m k1,...,km 行列所得的 m × m m\times m m×m 矩阵, a ∗ = [ a k 1 a k 2 ⋮ a k m ] \pmb{a}^* = \begin{bmatrix}a_{k_1}\\a_{k_2}\\\vdots \\a_{k_m} \end{bmatrix} a∗= ak1ak2⋮akm 是 a \pmb{a} a 的第 k 1 , . . . , k m k_1,...,k_m k1,...,km 分量拼成的向量。从特征函数角度证明如下

4.2 分量独立性
-
独立性:若 X = [ X 1 , X 2 , … , X n ] ⊤ ∼ N ( a , B ) \pmb{X} = [X_1,X_2,\dots,X_n]^\top \sim N(\pmb{a,B}) X=[X1,X2,…,Xn]⊤∼N(a,B),以下陈述等价(注: 随机变量互不相关指没有线性关系,即协方差为0;独立指没有一切关系)- X 1 , X 2 , … , X n X_1,X_2,\dots,X_n X1,X2,…,Xn 相互独立
- X 1 , X 2 , … , X n X_1,X_2,\dots,X_n X1,X2,…,Xn 两两独立
- X 1 , X 2 , … , X n X_1,X_2,\dots,X_n X1,X2,…,Xn 两两互不相关
- B \pmb{B} B 为对角阵(即不同的两个元协方差为0)
-
证明: 1 ⇒ 2 1\Rightarrow 2 1⇒2 显然; 2 ⇒ 3 2\Rightarrow 3 2⇒3 是随机变量性质; 3 ⇒ 4 3\Rightarrow 4 3⇒4 是互不相关定义;只需证明 4 ⇒ 1 4 \Rightarrow 1 4⇒1 即得四者等价

4.3 线性变换
一组正态分布随机变量的线性组合(多元正态随机向量的线性变换)仍然服从正态分布-
设有 n n n 元随机向量 X ∼ N ( a , B ) \pmb{X}\sim N(\pmb{a,B}) X∼N(a,B),则对 ∀ l ≠ 0 ∈ R n \forall \pmb{l}\neq \pmb{0} \in\mathbb{R}^n ∀l=0∈Rn 有
l ⊤ X ∼ N ( l ⊤ a , l ⊤ B l ) \pmb{l^\top X}\sim N(\pmb{l^\top a},\pmb{l^\top B l}) l⊤X∼N(l⊤a,l⊤Bl) 这里 l ⊤ X = ∑ i = 1 n l i X i \pmb{l^\top X} = \sum_{i=1}^n l_iX_i l⊤X=∑i=1nliXi 其实就是对 X \pmb{X} X 中所有正态随机变量 X i X_i Xi 线性组合得到的一元正态随机变量。上式从特征函数角度可证明如下

注意,这里 φ x ( t l ) \varphi_{\mathbf{x}}(t\pmb{l}) φx(tl) 是 n 元正态分布的特征函数; φ l ⊤ x ( t ) \varphi_{\mathbf{l^\top x}}(t) φl⊤x(t) 是一元正态分布的特征函数,最后要落到这个上 -
设有 n n n 元随机向量 X ∼ N ( a , B ) \pmb{X}\sim N(\pmb{a,B}) X∼N(a,B), C \pmb{C} C 为 m × n m\times n m×n 矩阵,且行向量线性无关,则
C X ∼ N ( C a , C B C ⊤ ) \mathbf{CX} \sim N(\mathbf{Ca},\mathbf{CBC^\top}) CX∼N(Ca,CBC⊤) 其实这里 C \pmb{C} C 中的每一行都对应了一个 1 中的线性组合。上式可以用特征函数证明如下
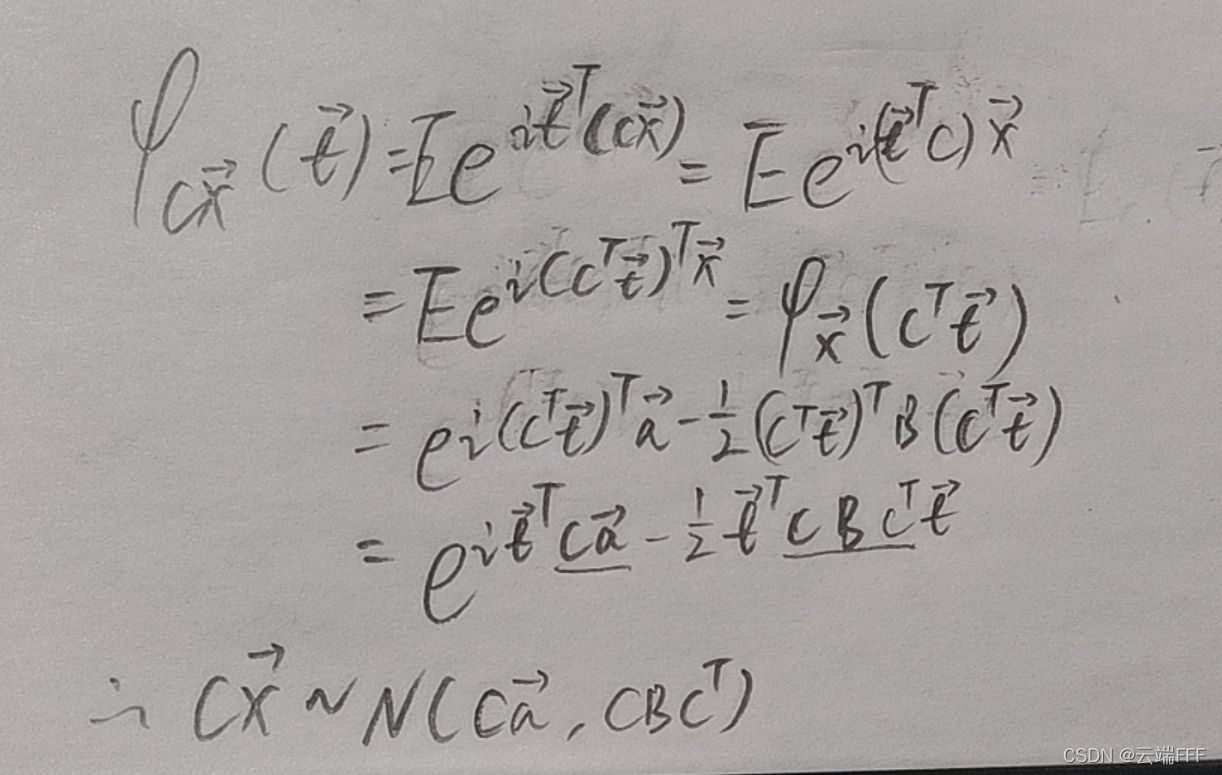
注意, φ x ( C ⊤ t ) \varphi_{\mathbf{x}}(\pmb{C^\top t}) φx(C⊤t) 表示的是 n n n 元正态分布的特征函数; φ C x ( t ) \varphi_{\mathbf{Cx}}(\pmb{t}) φCx(t) 表示的是 m m m 元正态分布的特征函数( C m × n \pmb{C}_{m\times n} Cm×n 将 n n n 元的 x \pmb{x} x 变换为 m m m 维),最后要落到这个上
-
5. 综合例题




开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献37条内容
已为社区贡献37条内容





所有评论(0)