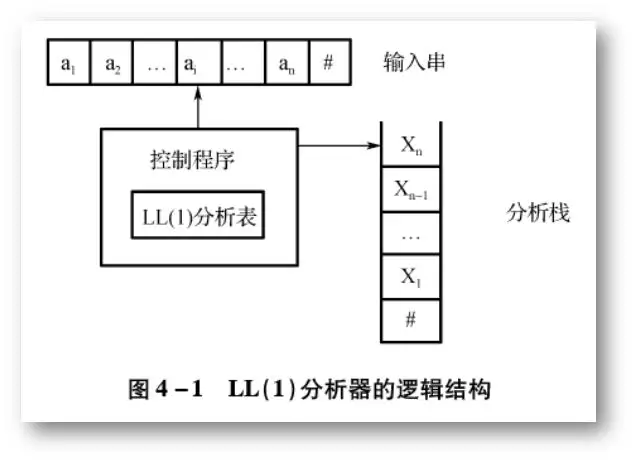
怎么写解题步骤——FIRST集、FOLLOW集、LL(1)分析法【编译原理之语法分析】
关键字:编译原理、语法分析、LL(1)分析法、LL(1)分析表、FIRST集、FOLLOW集、LL(1)例题的详细求解。
✅ 关于《编译原理》之 语法分析 的一点个人心得和总结。
本文已将 复杂的定义 → 易懂的讲解。
一、FIRST集
● FIRST集的写法为: FIRST( … ) = { … }
● FIRST集的定义为: FIRST(α) 是 α 的所有可能推导出来的 终结符号 或 ε 。【其中 α 是一个符号,也可能是一个符号串】
● 例如: 设文法 G[S]: S→aS|Ab|ε,A→bB|c,B→d|ε
那么 FIRST(B)={d, ε},FIRST(A)={b,c},FIRST(S)={a,b,c, ε}。
● 其实推导 FIRST集 有一定的算法,但是我们经过眼睛看,一般都能看出来。所以就不详细展开了,详见百度百科:First集合
● 补充说明: FIRST(aS) = {a},FIRST(Ab)=FIRST(A)={b,c},FIRST( ε )={ε},FIRST( c )={c}
二、FOLLOW集
● FOLLOW集的写法为: FOLLOW( … ) = { … }
● 对 FOLLOW集 的解释:也就是说,在一个文法中,FOLLOW(A) 即代表 → 在该文法能推导出来的所有句型 (比如:a、b、ab、Aa、Abc、ACa、AeB、ε、…) 中,所以直接在字符 A 之后的 终结符号集合 ( 就像前面的 a、b、e、… 所构成的集合 ),如果 A 是 开始符号,它的 FOLLOW集 还有多一个 #,记住就行了。
● 集合 FOLLOW(A) 的详细定义如下:
(1)若 A 是开始符号,则 # 就在 FOLLOW(A) 中。
(2)若存在产生式 B → αAβ ,则 FIRST(β) - {ε} 在 FOLLOW(A) 中。【其中 α和β 可能是非终结符号,也可能是终结符号】
(3)若存在产生式 B → αAβ ,且 ε 在 FIRST(β) 中,则 FOLLOW(A) 包含 FOLLOW(B)。【其中 α和β 可能是非终结符号,也可能是终结符号】
● 例如: 设文法 G[S]: S→aAb|AB,A→bB|c,B→d|ε,试求 FOLLOW(A) 和 FOLLOW(B)
然后根据 规则(1):
# ∈ FOLLOW(S) ,则 FOLLOW(S) = { # }
接着根据 规则(2):
b ∈ FOLLOW(A) ,则 FOLLOW(A) = { b }
FIRST(B) - {ε} ∈ FOLLOW(A) ,则 FOLLOW(A) = {b, d} 【注:FIRST(B) 可以用眼睛看出 】
接着根据 规则(3):
ε ∈ FIRST(B),则 FOLLOW(S) ⊆ FOLLOW(A),则 FOLLOW(A) = {b, d, #}
对于 “A→bB” 而言,相当于 “A→bBε”,所以 FOLLOW(A) ⊆ FOLLOW(B),则 FOLLOW(B) = {b, d, #}
● 个人总结:
① 规则(1) 较为简单,略过。
② 对于 规则(2) 来说,相当于用眼睛遍历 每一个产生式的 右 部 ,先看是否有像 Sb 一个大写字母(非终结符号)在前,一个小写字母(终结符号)在后的情况,有的话抓出来。显然 b 肯定属于 FOLLOW(S)。
然后再去看否有像 AB 两个大写字母(非终结符号)一前一后地紧挨着的情况,有的话也抓出来。显然 B 的 FIRST(B) 肯定属于 FOLLOW(S),这里动动大脑即明白,但是需注意的是 FOLLOW集 不包含 ε,也是记住就行了。
③ 对于规则(3) 来说,相当于用眼睛遍历 每一个产生式的 左 部和 右 部 ,如果有像 S → …A… 这样的产生式,那就看 A 的右边有一个什么,
如果 没有符号,那么显然 FOLLOW(S) ⊆ FOLLOW(A)【比如说,有一个符号串 xSyy,那么由上述产生式能推导出 x…Ayy,即 y 原先只属于 FOLLOW(S),现在 y 也属于 FOLLOW(A)】;
如果有一个 非终结符号,那么看这个非终结符号能否推导成 ε,可以的话就和上一个 “如果” 的情况相同;
如果有一个 终结符号,那么显然 FOLLOW(S) ⊈ FOLLOW(A)。【假设 S → …A… 为 “S → …Ac” ,那么对于一个符号串 xSyy,那么由上述产生式只能推导出 x…Acyy,显然 y 不属于 FOLLOW(A)】
三、LL(1)分析法
● LL(1)分析法是一种 自顶向下 不带回溯的语法分析方法。
● 这个讲清楚它的思想感觉蛮花时间的。这里借助一道题来讲解。

● 问题(1):FIRST集 和 FOLLOW集 的分析就不写了,按照前面的规则来做即可。

● 问题(2):
● 首先 LL(1) 文法有一些性质,这里写一下:它不带回溯(即没有类似 S → aB|aC 的情况),它不含左递归(即没有类似 S → Sa 的情况)。
● 接下来给一下细节的定义,当且仅当文法 G 中同一终结符号的任意两个规则 A → α | β 满足以下三个条件,文法 G 才是 LL(1) 文法:【其中 α和β 可能是非终结符号,也可能是终结符号】
① FIRST(α) ∩ FIRST(β) = ∅
② α 和 β 中最多只有一个可能推出 ε。
③ 如果 β 是 ε 或能推导出 ε,那么 α 推导出的任何串不能以 FOLLOW(A) 中的终结符号开始。反之,如果 α 是 ε 或能推导出 ε,那么 β 推导出的任何串不能以 FOLLOW(A) 中的终结符号开始。
● 为什么要有这三条性质呢?因为为了避免 “回溯” 和 “左递归”,这是前人总结的经验之谈。其实有详细的原因,但一两句话讲不清楚,先记住吧。
● 接下来就以这三条性质来解 问题(2)。

● 问题(3):
● 构造文法分析表也有一定的规律,一般 先依据 FIRST集 来构造第一遍,然后 再依据 FOLLOW集来构造第二遍。
● 值得注意的是!!!!!敲黑板!!!!!这里用的 FIRST集 全是来自于产生式右边,不是来自于产生式左边。
● “先依据 FIRST集 来构造第一遍” 的方法:先把所有产生式右边的 FIRST集 求出来,然后一个一个地对着看。比如说,我们用眼睛扫描到 “FIRST(+E) = {+}” 时,就找到 “+” 号这一列,然后再去文法 G[E] 中去找哪一条产生式能推出 +E,噢,原来是 “E’→+E”,那就把它写进 “ E’ ” 对着那一行,“ + ” 对着那一列 的位置去。

● “再依据 FOLLOW集来构造第二遍” 的方法:在文法 G[E] 中一个一个地看,对有 ε 的产生式就要留意了。比如说,我们用眼睛扫描到 “E’ → +E|ε ” 时,我们只用关心 “E’ → ε ” 即可。然后找到 FOLLOW(E’)={ #, ) },接着依次把 “ #、) ” 对着的那一列,且 “ E’ ” 对着的那一行的单元格,填入 “E’ → ε ”。

● 等等!!!别以为 LL(1)分析表已经构造完了!!! 初学者往往还会遗漏 “隐式 ε 的情况”!!!我们需要检查一下!
● 比如说,上面的 “ E ::= TE’ ”,假如 “ T ” 可以推出 ε,且 “ E’ ” 也可以推出 ε,那么 “ E ” 也可以间接地推出 ε。
● 那么 “ E ::= TE’ ” 也要做和上面 “红圈①” 做同样的处理。如下表所示:

● 但是上表,不存在 “隐式 ε 的情况 ”,所以最终的 LL(1)分析表 如下:

● OK,分析表构造完了,接着用该分析表来分析符号串 a*b+b 属不属于文法 G[E]:
● 怎么写的呢?简单说几个要点:
① 先写 “步骤”、“分析栈”、“余留输入串”(即是我们待分析的符号串)、“所用的产生式” 这几个字。
② “步骤” 那一栏相当于 序号。
③ “分析栈” 一开始里面装有 “#” 和 开始符号(这里是“E”)。
④ “余留输入串” 一开始里面装有待分析的符号串(这里是“a*b+b”) 和 “#”。
⑤ “#” 是一个 “栈底符号”,如果一个栈的样子形如 “#…”,那说明左边是栈底;如果一个栈的形如 “…#”,那说明右边是栈底。
⑥ 对于 “栈” 来说,遵守 “先进后出” 原则。
⑦ “所用的产生式” 全部来自于 LL(1)分析表,就是上面构造的那张表。
⑧ 一开始,“分析栈” 的 “E” 正对 “余留输入串” 的 “a”,查表可知 Table[E, a] = “ E→TE’ ”,那么在产生式那里写 “ E→TE’ ”。
⑨ 然后,“ E ” 在下一步(步骤2)中出栈,“ TE’ ” 进栈,注意进栈的顺序。
⑩ 接着,“分析栈” 的 “T” 正对 “余留输入串” 的 “a”,查表可知 Table[T, a] = “ T→FT’ ”,那么在产生式那里写 “ T→FT’ ”。
⑪ 然后,“ T ” 在下一步(步骤3)中出栈,“ FT’ ” 进栈,注意进栈的顺序。
⑫ 接着,“分析栈” 的 “F” 正对 “余留输入串” 的 “a”,查表可知 Table[F, a] = “ F→PF’ ”,那么在产生式那里写 “ F→PF’ ”。
⑬ 然后,“ F ” 在下一步(步骤4)中出栈,“ PT’ ” 进栈,注意进栈的顺序。
⑫ 接着,“分析栈” 的 “P” 正对 “余留输入串” 的 “a”,查表可知 Table[P, a] = “ P→a ”,那么在产生式那里写 “ P→a ”。
⑬ 然后,“ P ” 在下一步(步骤5)中出栈,“ a ” 进栈。此时,“分析栈” 和 “余留输入串” 的 “a” 刚好两两相对,在下一步就将消去。
⑬ 接着,“分析栈” 的 “ F’ ” 正对 “余留输入串” 的 “ * ”,查表可知 Table[F’, *] = “ F’→*F’ ”,那么在产生式那里写 “ F’→*F’ ”。
…后面的步骤类似
…直到两个 “#” 碰头。如果不能碰头就说明该串不能由该文法构成。反之则可以。

四、写后感
● 在写这篇博客的过程中,感觉真的很难写好,我省略了很多 “为什么”,只写了 “怎么做”
● 还有,构成 LL(1)分析表的过程中有很多坑,特别是在构造 FOLLOW集 的时候,需要多写写,多试错。
● 还是老师讲得好啊 ::>_<::,给 沙c 老师点赞!
● 如果不足,欢迎评论区留言讨论
⭐️ ⭐️

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献22条内容
已为社区贡献22条内容





所有评论(0)