1、前言

本文将对PGGAN这个模型进行原理解析，该模型是生成模型，与GAN一样，他也同样可以伪造数据（如图像），区别在于，这个模型算是GAN的进阶版，其克服了GAN模型中的很多问题

视频：【伪造高清人像——PGGAN原理解析-哔哩哔哩】

2、GAN模型存在的问题

2.1、模式崩溃（mode collapse）

在GAN训练的过程中，及其容易出现模式崩溃的问题——生成数据只是原始数据的子集，比如对于手写数字数据集，我们训练完后，然后使用生成器生成手写数字，生成的数字往往只有那么几个，比如1，7，9，而对于其他的数字，生成器几乎不会生成。比如下图

造成这个问题的主要原因，大概是在训练的过程中，生成器突然发现生成1，7，9这几个数字给判别器，判别器往往不能够正确区分，于是生成器就往这几个数字靠近，只生成这几个数字，进而产生mode collapse.

2.2、GAN很难训练高分辨率的图片

传统的GAN而言，训练那种28 x 28的低分辨率的图片雀食不成问题，如上面的手写数据集。然而，一旦训练1024 x 1024 这种高清大图，生成器G在一开始往往不能生成这种高分辨率的图像，于是对于判别器而言，几乎一眼就能够区分出来。于是乎，在反向传播的时候，会反馈出极大的梯度，造成生成器参数出现大范围的更新，这种更新是及其危险的，非常容易造成生成器崩溃。

除此以外，对于高分辨率的图片，由于设备环境的内存限制，我们往往只能够使用较小的batch_size（一次喂给网络多少张图片），这更加加剧了不稳定性。

3、PGGAN的改进点

3.1、渐进式训练

PGGAN的论文标题：Progressive Growing of GANs for Improved Quality, Stability, and Variation

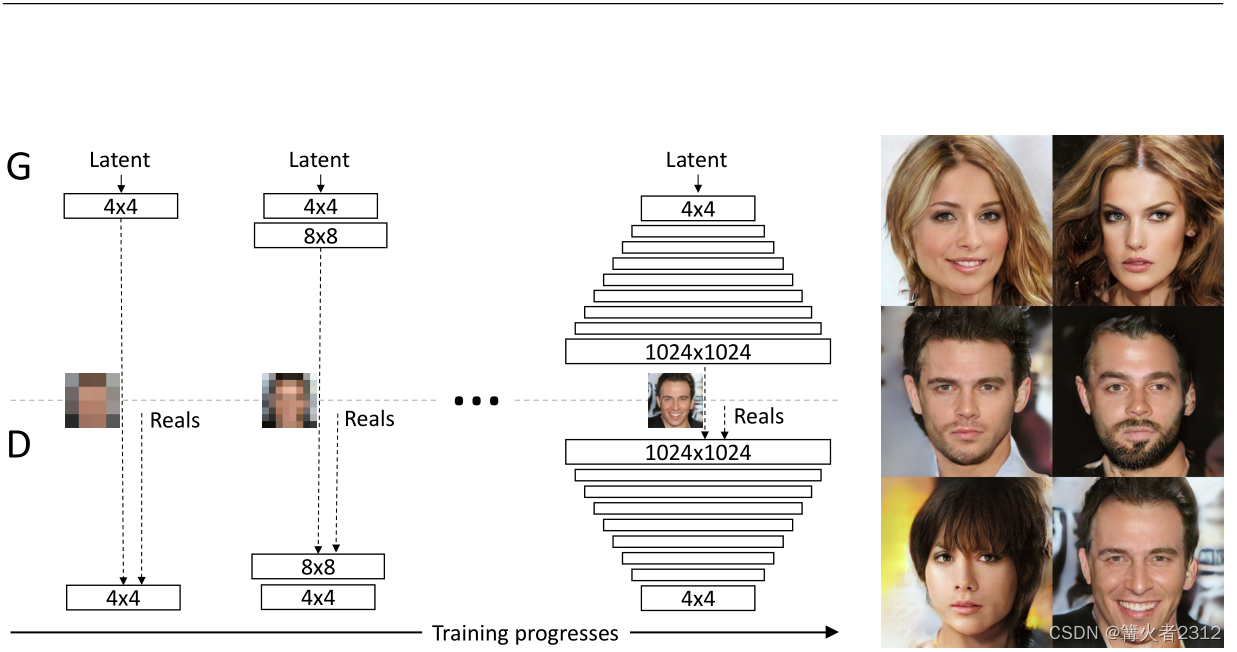
意为渐进式的GAN以提升质量，稳定性和多样性，顾名思义，其实就是对于高分辨率的图片，我们先从它的低分辨率开始训练，然后再逐层提高分辨率进行训练。具体我们来看下面这张图

（Ps：此图片来自原论文）看不懂？我知道你很急，但你先别急，容我速速道来！

首先，将图像分为左右两部分，左边的流程图，而右边的图像则为结果图。对于左边，中间有一条线，将上下两部分分开，将其分为生成器G和判别器D两部分，而中间那张图片记为在当前情况下生成的图像。另外，里面的 $\boxed{N\times N}$ 代表的是分辨率，比如里面的$\boxed{4\times 4}$代表的就是图像分辨率为 4 x 4 。

首先，我们先训练 4 x 4 分辨率时的图像，即

可以看到，训练完后，在4 x 4分辨率的情况下，生成的只有人像的大概的轮廓。接着，我们在 4 x 4 的基础上，将分辨率提高到 8 x 8 ,然后训练，得到的图像明显是增加了一些细节

​ 最后，我们不断提高分辨率，不断训练，当分辨率提高到 1024 x 1024 的时候，不难看到，生成的图像已经是的高清且逼真的高清大图啦

那么，接下来就由一个问题了，我们该如何，在训练完 4 x 4 分辨率之后，去提高成 8 x 8 呢？ PGGAN的做法就是，平滑地将 8 x 8 接入到 4 x 4 里面 。

具体而言，我们来看

即，我们从 4 x 4 的特征图（即feature map，形状为【batch_size, chancel_num, 4, 4】不懂的话，请看视频）开始，然后将其进行两次上采样（采样方法随你选，不懂的话，请看视频），然后得到 8 x 8 的特征图，我们把左边的 8 x 8 的特征图使用一个 1x1 的卷积核转化为图像（三通道，RGB，形状为【batch_size,3, 8, 8】）,得到图像A。

接着，我们再把另一张 8 x 8 的特征图进行卷积块block（后面会给出结构图）处理，然后再同上一样转为图像B

最后，就到了上面提到的平滑接入，即对于图像B，我们设定一个超参数$\alpha$（$\alpha$从0开始，随着训练不断增大），所以，有 $\alpha \ast 图像B+(1-\alpha )\ast 图像A=图像C$)

这个公式很容易理解，在一开始的时候，我们更愿意相信 4 x 4直接上采样的图像，而随着$\alpha$的增大，我们则更偏向经过卷积层block训练后的图像。

同理，对于判别器而言，此时它接收的输入是 8 x 8 ，他就要下采样。总之一切都和生成器反过来。所以，最终的流程图如图所示（以下为论文中16渐进到32的流程）

这种训练方式的好处主要有三点：

①提高图像质量。这种增量训练能够首先发现图像的大体结构（Ps：低分辨率时），然后将注意力转移到图像的细节上（Ps：高分辨率时），而不是必须同时学习所有大体结构和细节。

②提高训练的稳定性。在早期，PGGAN首先是在很小分辨率的图像上进行训练，这大大减少了生成器崩溃的可能性，因为低分辨率有更少的类别信息和细节的信息。

③减少训练时间。根据论文作者进行的试验表明，这种训练方式，将训练时间降低了2~6倍。

3.2、均衡学习率（Equalized Learning Rate）

对于模型里面的参数$w$，作者在开始的时候对其进行$N(0,1)$初始化，也就是$w$的初始值从标准正态分布里面进行采样。但是，在模型训练的过程中，且又单独对某一层（比如第i层）的参数$w$进行了处理，处理方式为
$${\hat{w}}_i=w_i/c_i$$
(Ps:此处是除法，但是我在很多PGGAN代码实现中看到的却都是乘法)

其中$w_i$为原始的参数，${\hat{w}}_i$为处理后的参数值，$c_i$为He初始化在第i层的标准差，在一般情况下
$$c_i=\sqrt{\frac{2}{n_i}}$$
$n_i$表示第输入神经元的数量。

作用：

根据论文，每一次进行推断时都使用该公式，可以让里面的权重在同一单位长度下进行更新，从而每一次当第 i 层里面$w$之间存在的尺度差（有些$w$需要更大尺度地更新，而有些则只需要更小尺度地更新）。

3.3、像素特征向量的归一化（Pixel Normalization）

为了防止判别网络和生成网络竞争而产生崩溃的情况，论文提到，在每一个卷积层后面，都会在空间维度上（channel_num）进行向量归一化，具体公式为
$$b_{x,y}=a_{x,y}/\sqrt{\frac{1}{N}\sum _{j=0}^{N-1}(a_{x,y}^j{)}^2+ϵ}$$
这里的$a_{x,y}、b_{x,y}$分别代表原始向量特征和归一化后的向量特征，$ϵ=10^{-8}$，$N$为特征图（feature map）个数。

如果你问我，为什么是这样？为什么这样可以防止训练的崩溃？那你可算是问对人了，作者在论文里面写道——“We find it surprising that”，看起来，他们就像是知道归一化能够缓解输出量之间的差别程度，减少崩溃的可能。但是却又不想用传统的归一化的方法，于是自创一种归一化的方法。

在钞能力的强大作用下（我英伟达有的是卡，显卡按斤算！Ps：作者来自英伟达哦）（刘德华：干嘛？让隔壁老外看到还以为我吃不起显卡呢？再来一吨！一人一吨！傻啦吧唧的！😡），他们惊讶的发现，这种归一化方法并没有损害生成器，但是，对于大多数数据集，这种方法并没有太大改变最终的结果（很显然，作者进行了大量的消融实验）。

接着，再引用论文里面的一句话——“but it prevents the escalation of signal magnitudes very effectively when needed.”，当需要的时候，这种方法能够让特征值尺度一致，并且防止数值溢出。（翻译是防止信号幅度增加，小子才疏学浅，不大理解，我姑且认为就是如此吧，有懂哥给解释下，万般感谢，给您跪了！）。

3.4、使用小批量标准差增加生成样本的多样性（minbatch）

其实这种方法并不是这篇论文首创的，作者只是引用。但是，作者却对这个方法就行了一些调整。从而让本该引入新参数的方法（该方法的原始方法需要引入新参数），变得不再需要。具体而言

假如，我们的一次喂给判别器的图片为64（batch_size）张，在最后一个Conv block块，直接在batch_size这个维度上求标准差，然后，对所有维度求均值，得到单一个值。然后把这个单一的值扩维（复制）成【batch_size , 1 , h , w】的向量。最终我们把这个向量同原始数据进行拼接（在chancel维度进行）。具体，可以看后面的网络结构图。

接着，我们来直觉地去理解这种做法为什么能够增加样本的多样性

我们一次性喂给判别器的图像，必然是打乱之后的，里面应当是有各个类别的手写数字，我们对这些图片在batch_size这个维度上求标准差，就是求出这些图片的差异，然后再求出均值。很显然，这里的均值其实就是差异的大小程度了。

上面是对于真实样本的，那么对于伪造的样本呢？如果伪造数据的均值和真实的均值不一样，那么是不是判别器就可以很显然根据这个均值判断出来。于是乎，在这种情况下，生成器生成的样本所对应的均值，不得不向真实数据的均值靠近。生成器生成样本的均值一旦向真实数据的均值靠近，就证明这些伪造图片的多样性和真实图片的多样性是一样的呀。所以，只要真实图片的每一个batch_size具有多样性，那么便可以解决这些问题啦！

3.5、对判别器的损失加上一个极小的权重项

对于初始的GAN，在一开始或者运行的过程中，一旦它很容易判别出真伪图片，那么及其容易导致损失为0，产生梯度消失的现象，因此，作者给判别器加上了一个极小的权重项
$$\hat{L}=L+{ϵ}_{drift}{\mathbb{E}}_{x\sim {\mathbb{P}}_r}[D(x{)}^2]$$
其中$L、\hat{L}$分别代表初始的损失和加上极小权重项的损失。${ϵ}_{drift}=0.001$，${\mathbb{P}}_r$代表原始数据，$\mathbb{E}$代表数学期望，$D(x)$表示判别网络对$x$进行真伪判断输出的概率。

4、PGGAN网络结构

论文里面是给出了对于CELEBA-HQ这个数据集的网络结构，并且，其实在上面提到的3.5里面，也是在这个数据集上面应用的，论文并没有将其作为一个新的点

左边是生成器G，右边就是判别器G（这不费发吗，上面都写着，但我还是要说，不服顺着网络过来噶我）

下面我们做个简单的介绍

以圈起来的这一部分为例，Latent vector 就是从简单的分布种采用出来的向量（一般是从标准正太分布中采样）。而采样出来的维度在右边，则为 512 x 1 x 1。

再来看 Conv 4 x 4 代表的就是 4 x 4 为卷积核的卷积层，在这个卷积层的右边，有一个LReLU，其代表leaky ReLU激活函数，并且其 leakiness 为 0.2。再有，对于有偏置项b的层，其初始化都为0。生成器上采样采用元素复制，判别器下采样采用平均池化。

5、结束

更多细节，请阅读论文。如有问题，还望指出，阿里嘎多！