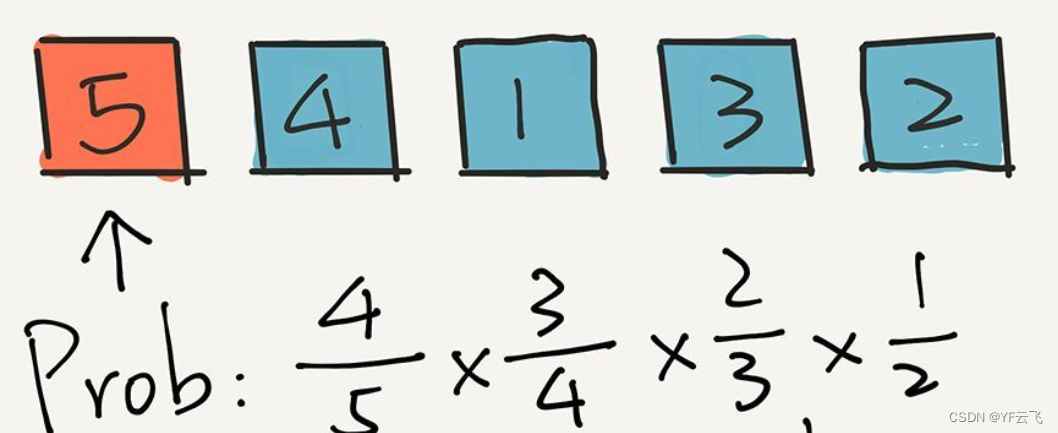
游戏洗牌算法——常用+详解最优Knuth_Durstenfeld算法
游戏常用算法-洗牌算法
目录
前言
洗牌算法是一个比较常见的面试题。
一副扑克54张牌,有54!种排列方式。而最佳的洗牌算法,应该能够等概率地生成这54!种结果中的一种。
基于Unity的洗牌算法代码实现
内容
抽牌洗牌
原理
这是完全合乎现实洗牌逻辑的算法。
就是抽出纸牌的最后一张随机插入到牌库中,这般抽54次就完成了对扑克牌的洗牌。
复杂度
空间O(1),时间O(n^2)
优缺点
优点:逻辑简单。
缺点:如果牌库是以一个数组描述,这种插入式的洗牌不可避免地要大量移动元素。
Fisher_Yates算法
原理
取两个列表,一个是洗牌前的序列A{1,2….54),一个用来放洗牌后的序列B,B初始为空
while A不为空
随机从A取一张牌加入B末尾
复杂度
空间O(n),时间O(n^2)
代码实现
List<int> list = new List<int>(pukes.pukes);//洗牌前的序列A
List<int> newlist = new List<int>(list.Count);//洗牌后的序列B
for(int i = 0 ; i < pukes.pukes.Length ; ++i)
{
int randomIndex = Random.Range(0, list.Count);
int r = list[randomIndex];//随机取牌
newlist.Add(r);
list.RemoveAt(randomIndex);
}
pukes.ResetPuke(newlist.ToArray());//序列B为洗牌后的结果优缺点
优点:算法原理清晰,通过54次生成的随机数取1/54,1/53,…1/1能等概率地生成这54!种结果中的一种。
缺点:额外开辟了一个List,而且为List删除元素是不可避免地需要移动元素。
Knuth_Durstenfeld算法(最佳洗牌算法)
Knuth 和Durstenfeld 在Fisher 等人的基础上对算法进行了改进。 每次从未处理的数据中随机取出一个数字,然后把该数字放在数组的尾部, 即数组尾部存放的是已经处理过的数字 。 这是一个原地打乱顺序的算法,算法时间复杂度也从Fisher算法的 O ( n 2 )提升到了 O ( n )。
for(int i = pukes.pukes.Length - 1;i>0;--i)
{
int randomIndex = Random.Range(0, i+1);
pukes.Swap(randomIndex, i);
}void Knuth_Durstenfeld_Shuffle(vector<int>&arr)
{
for (int i=arr.size()-1;i>=0;--i)
{
srand((unsigned)time(NULL));
swap(arr[rand()%(i+1)],arr[i]);
}
} 详解
是时候仔细的看一下,这个简单的算法,为什么能做到保证:对于生成的排列,每一个元素都能等概率的出现在每一个位置了。
其实,简单的吓人:)
在这里,我们模拟一下算法的执行过程,同时,对于每一步,计算一下概率值。
我们简单的只是用 5 个数字进行模拟。

那么,根据这个算法,首先会在这五个元素中选一个元素,和最后一个元素 5 交换位置。

下面,我们计算 2 出现在最后一个位置的概率是多少?非常简单,因为是从 5 个元素中选的嘛,就是 1/5。

下面,根据这个算法,我们就已经不用管 2 了,而是在前面 4 个元素中,随机一个元素,放在倒数第二的位置。假设我们随机的是 3。

下面的计算非常重要。3 出现在这个位置的概率是多少?计算方式是这样的:

其实很简单,因为 3 逃出了第一轮的筛选,概率是 4/5,但是 3 没有逃过这一轮的选择。在这一轮,一共有4个元素,所以 3 被选中的概率是 1/4。因此,最终,3 出现在这个倒数第二的位置,概率是 4/5 * 1/4 = 1/5。
还是 1/5 !
实际上,用这个方法计算,任意一个元素出现在这个倒数第二位置的概率,都是 1/5。
到这里已经大概了解了。我们再进行下一步,在剩下的三个元素中随机一个元素,放在中间的位置。假设我们随机的是 1。

关键是:“ 1 ”出现在这个位置的概率是多少?计算方式是这样的:

即 1 首先在第一轮没被选中,概率是 4/5,在第二轮又没被选中,概率是 3/4 ,但是在第三轮被选中了,概率是 1/3。乘在一起,4/5 * 3/4 * 1/3 = 1/5。
用这个方法计算,任意一个元素出现在中间位置的概率,都是 1/5。
这个过程继续,现在,我们只剩下两个元素了,在剩下的两个元素中,随机选一个,比如是4。

然后,4 出现在这个位置的概率是多少?4 首先在第一轮没被选中,概率是 4/5;在第二轮又没被选中,概率是 3/4;第三轮还没选中,概率是 2/3,但是在第四轮被选中了,概率是 1/2。乘在一起,4/5 * 3/4 * 2/3 * 1/2 = 1/5。
用这个方法计算,任意一个元素出现在第二个位置的概率,都是 1/5。

最后,就剩下元素5了。它只能在第一个位置呆着了。
那么 5 留在第一个位置的概率是多少?即在前 4 轮,5 都没有选中的概率是多少?
在第一轮没被选中,概率是 4/5;在第二轮又没被选中,概率是 3/4;第三轮还没选中,概率是 2/3,在第四轮依然没有被选中,概率是 1/2。乘在一起,4/5 * 3/4 * 2/3 * 1/2 = 1/5。

算法结束。
你看,在整个过程中,每一个元素出现在每一个位置的概率,都是 1/5 !
所以,这个算法是公平的。
当然了,上面只是举例子。这个证明可以很容易地拓展到数组元素个数为 n 的任意数组。整个算法的复杂度是 O(n) 的。
通过这个过程,大家也可以看到,同样的思路,我们也完全可以从前向后依次决定每个位置的数字是谁。不过从前向后,代码会复杂一些。
(因为生成 [0, i] 范围的随机数比生成 [i, n) 范围的随机数简单,直接对 i+1 求余就好了)
Inside_Out算法
C++ stl中random_shuffle使用的就是这种算法。
原理
在[0, i]之间随机一个下标j,然后用位置j的元素替换掉位置i的数字。
通过54次生成的随机数取1/1,1/2,…1/54能等概率地生成这54!种结果中的一种。
复杂度
空间O(1),时间O(n)
代码实现
public static void Shuffle(Pukes pukes)
{
int len = pukes.pukes.Length;
for (int i = 0; i < len; ++i)
{
int randomIndex = Random.Range(0, i + 1);
pukes.Swap(i, randomIndex);
}
}详解请参考:PCFG中inside和outside算法详解_算法码上来的博客-CSDN博客
random_shuffle
关于c++ stl 的random_shuffle。
它的算法原理和Knuth_Durstenfeld类似。
先从所有元素中选一个与位置1的元素交换,然后再从剩下的n-1个元素中选择一个放到位置2,以此类推。
测试代码如下:
#include <iostream>
using namespace std;
#include <algorithm>
#include <vector>
#include <ctime>
class myPrint
{
public:
void operator()(int val)
{
cout << val << " ";
}
};
void test01()
{
srand((unsigned int)time(NULL));
vector<int> v;
for(int i = 0 ; i < 10;i++)
{
v.push_back(i);
}
for_each(v.begin(), v.end(), myPrint());
cout << endl;
//打乱顺序
random_shuffle(v.begin(), v.end());
for_each(v.begin(), v.end(), myPrint());
cout << endl;
}
int main() {
test01();
system("pause");
return 0;
}
此方法比较实用,使用时记得加随机数种子。
总结
算法从来不是枯燥的逻辑堆砌,而是神一样的逻辑创造。
尽管这个世界很复杂,但竟也如此的简洁,优雅。
一起加油!

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献7条内容
已为社区贡献7条内容





所有评论(0)