点云特征提取算法之ISS

代码链接 : ISS

Github链接：有关于环境感知方面的网络介绍及代码链接

特征点的定义参考这篇博文角点（corner point）、关键点(key point)、特征点(feature point):

在图像处理中，所谓“特征点”，主要指的就是能够在其他含有相同场景或目标的相似图像中以一种相同的或至少非常相似的不变形式表示 图像或目标 ，即是对于同一个物体或场景， 从不同的角度采集多幅图片 ，如果相同的地方能够被识别出来是相同的，则这些点或块称为特征点。

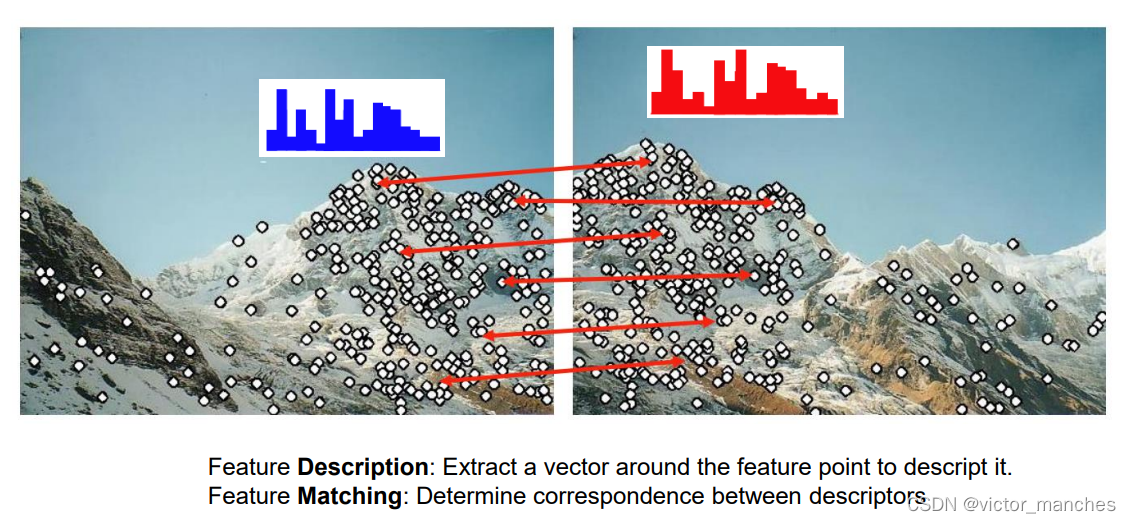
如上图，两张不同的图之间的特征点的描述和匹配，可以用来做三维重建，姿态估计，全景图的构造以及SLAM的应用，具有极大的发展前进。

在深度学习普及之前大部分都是由传统算法提取特征点，如下图，传统算法的代表主要由通过图像特征的Harris 算法， SUSAN算法 以及SIFT ，还有基于3D点云特性本身的ISS算法。本文主要以介绍ISS算法为主

深度学习没有普及主要原因: 特征点的描述比较模糊，可能由观察的角度决定eg去观察一辆车的时候，轮胎上的花纹可能是特征点，但是当观察角度变成整条马路上所有车之后，这些花纹就不再是特征点了。所以导致特征点的定义模糊，所以导致没有现成的数据集，所以目前的都是一些无监督的方法。

算法简介

ISS是直接针对于点云数据的特征提取方法，其思想的核心在于PCA分解之后，其最小的特征值必须要足够大。基于这个思想我们对算法进行介绍:

1. 对点云的每个点遍历，计算其RadiusNN

   
   

2. 每个点根据其RadiusNN表示，并由其R近邻点计算加权的协方差矩阵

   1. 权重wj构建的思想基于: 稀疏部分的点云的权重大于密集部分的点云权重,所以定义如下对于任意一个近邻点j，其对应的矩阵与点j的R近邻的个数成反比
   
   2. 最终的加权协方差矩阵定义如下:

3. 对协方差矩阵进行特征值分解，分别计算λ1,λ2,λ3,降序排序

   
   

4. 计算完所有点的特征值后，进行过滤，过滤条件如下其中γ21 和 γ32都是超参数根据实验进行调整，其大致意思可以理解成，不仅仅需要λ3的值足够大，且需要λ1 λ2 和λ3个不相等:

   

5. 对λ3进行NMS(非极大值抑制)

   1. 根据λ3按照降序排序
   2. 取出λ3最大值作为参考点，并加入最终的结果中
   3. 对propose的点里去除掉与参考点距离小于r的点
   4. 重复步骤23，直至propose里所有点遍历完，取出最终结果则完成了NMS过程

代码实现

这里放了几个核心代码,具体代码参考github:

ISS初始化

    def __init__(self, pc , radius = 0.1, gama21 = 0.7 , gama32 =0.7 , min_lambda3 = 0.0008, min_neighbors = None):
        self.pc = pc #o3dpc
        self.tree = o3d.geometry.KDTreeFlann(pc) # KDTree
        self.point_clound = np.asarray(pc.points) 
        self.num_points = self.point_clound.shape[0]
        self.radius = radius # 计算特征点的直径
        self.gama21 = gama21
        self.gama32 = gama32
        self.min_lambda3 = min_lambda3

初始化涉及到几个超参数，包括radius , γ21 , γ32 和最小λ3的设置 以及最小近邻点的设置。

计算特征值

    def cal_eigen(self , point , idx_neighbors , w):
        #计算根据记录的加权的radius近邻协方差矩阵
        w = 1 / np.array(w) # K
        dis = self.point_clound[idx_neighbors] - point #每个点距离query_point的相对距离 , K * 3
        conv = np.dot((dis.T * w), dis) / w.sum() # 与其相对距离成反比，与其周围点的个数成反比
        #计算特征值
        values, v = np.linalg.eig(conv)
        values  = values[np.argsort(values)[::-1]]
        return values

这里实现的是加权的协方差矩阵的构造，对每个点计算其近邻点，然后每个近邻点计算近邻点的个数，从而得到权重为个数的倒数，最终乘以L2距离，得到协方差矩阵。

NMS实现

    def NMS(self):
        #对特征点按照lambda3的值进行排序
        tmp = pd.DataFrame(self.points_eigns)
        start = len(tmp)
        tmp.sort_values('l3' ,ascending=False, inplace=True)
        tmp = tmp['id'].to_numpy().tolist()

        res = [] #用于保存最后的id
        # print(len(self.radius_neighbor))
        while (tmp):
            #取出lambda3最大的点,并加入结果中，还需要删除掉自身
            query_id = tmp[0] 
            res.append(query_id)
            tmp.remove(query_id)

            #找到query点的Rnn近邻，如果出现在tmp中全部删除
            rnn_list = self.radius_neighbor[query_id]
            jiaoji = set(tmp) & set(rnn_list) 

            for i in list(jiaoji):
                tmp.remove(i)
  
        #更新下特征点的id
        self.points_eigns['id'] = res
        end = len(res)
        print("NMS: %d"%( start - end))

有关NMS步骤上面讲的比较清楚，这里类似物体检测里的NMS，通过λ3对应置信度过滤掉propose ，通过计算r近邻对应IOU过大过滤掉同一物体，最终对于聚集密集的特征点有且仅取出一个点。

效果

数据集来自modelnet40 , 下面展示几个demo

Piano

可以看到点云从1000 -> Filter(2950) -> NMS(35),整体效果我觉得还可以,保留的特征点也比较多，参数就不细调了

Person

可以看到点云从1000 -> Filter(6490) -> NMS(47),对于人这种不是特别规则的形状，效果我觉得差一点，如果不看原图很难恢复。