1、前言

上一篇，我们讲了受限玻尔兹曼机的原理推导和代码实现，本文将介绍深度置信网络（DBN）的简单原理和算法流程，不会涉及过多的原理推导。
数学基础：【概率论与数理统计知识复习-哔哩哔哩】

2、模型

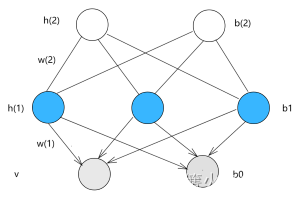
先来看以下结构图

图中分为三层$\boxed{\mathbf{一层可见层}\mathbf{v}，两层隐藏层\mathbf{h}(1)、\mathbf{h}(2)}$，实际上，它的隐藏层可以无限扩展，只是最后一层n和n-1层之间是无向图连接，而其余层皆是用有向图连接。

其参数为每一层的连接权重$w$，偏置$b$

对于DBN，$\boxed{其实可以理解为多个受限玻尔兹曼机（\mathbf{RBM}）叠加在一起}$，从而构成了DBN，但你会发现，在RBM种是无向图，而显然在DBN中，却是$\boxed{\mathbf{有向}+\mathbf{无向}}$。为何呢？

我们一步步地从RBM到DBN。

我们来看看传统的RBM

显然是无向图，我们在受限玻尔兹曼机中能够通过极大似然估计计算出对应的参数$\boxed{w(1),b_0,b_1}$。

得到了参数，我们就可以通过计算$P(h(1)|v)$，采样出隐藏层$h(1)$的样本。然后再将$h(1)$作为观测层，将$h(2)$作为隐藏层，然后将从$P(h(1)|v)$采样出来的样本作为训练数据，进行训练出参数$w(2),b(2)$

并且，我们还要将从$v$到$h(1)$的无向图改为从$h(1)$到$v$的有向图，至于为什么要这样做，我个人认为是因为极大似然估计要计算的是$P(h(1))$，而下面的$w(1)$是我们训练好出来的了，想要不改变它，那就是让$v$和$h(1)$单方面断绝父子关系$\boxed{\mathbf{单向}\mathbf{h}(1)\mathbf{是}\mathbf{v}的父节点，反之却不成立，也就是\mathbf{P}(\mathbf{h}(1))\mathbf{不受}\mathbf{v}的影响（我个人理解）}$。所以结构图就变成了

这样，就得到了我们模型图。然后我们以此法，也还可以得到下一层隐藏层和模型参数。以上，就是DBN的简单模型流程了。

但是仍然有个问题，那就是为什么这样的模型比RBM好？

3、优越性证明

假设我们的训练数据为$V$，单个样本$v^i\in V$，所以要求log极大似然估计
$$\log P(V)=\log \prod _{i=1}^{N}P(v^i)=\sum _{i=1}^N\log P(v^i)$$
我们对单个样本讨论，记为$P(v)$，记图中第一层隐层$h(1)$为$h^1$
$$\begin{array}{rl}\log P(v)=& \log \sum _{h^1}P(v,h^1)\\ =& \log \sum _{h^1}q(h^1|v)\frac{P(h^1,v)}{q(h^1|v)}\\ =& \log \left({\mathbb{E}}_{q(h^1|v)}\left[\frac{P(h^1,v)}{q(h^1|v)}\right]\right)\\ \ge & {\mathbb{E}}_{q(h^1|v)}\left[\log \frac{P(h^1,v)}{q(h^1|v)}\right]\\ =& \sum _{h^1}q(h^1|v)\left(\log P(h^1,v)-\log q(h^1|v)\right)\\ =& \sum _{h^1}q(h^1|v)\log P(v|h^1)P(h^1)-\sum _{h^1}q(h^1|v)\log q(h^1|v)\end{array}\text{\hspace{1em}(a)(b)}$$
其中（式a）到（式b）用到了Jensen不等式——$\boxed{对于一个凸函数而言，有\frac{\mathbf{f}({\mathbf{x}}_1)+\mathbf{f}({\mathbf{x}}_2)}{2}\ge \mathbf{f}(\frac{{\mathbf{x}}_1+{\mathbf{x}}_2}{2})}$

$\boxed{\mathbf{因为上面的}\log \mathbf{函数是以}\mathbf{e}为底的凹函数，所以反过来}$

不难看出，对$P(v)$求极大似然后，能够求出第一层的参数。对于里面的$\log P(v|h^1)P(h^1)=\log P(v|h^1)+\log P(h^1)$，前面我们说过，会将第一层参数的$w(1)$固定住，所以自然$P(v|h^1)$自然是不变的。而我们要改变的，就是$\log p(h^1)$，也就是求它的极大似然估计$\arg \max \log P(h^1)$。

$\boxed{\mathbf{通过计算}\mathbf{P}({\mathbf{h}}^1)的极大似然，可以计算出参数\mathbf{w}(2)以及相关的偏置项。}$
$\boxed{这样，我们就让\mathbf{P}(\mathbf{v})的下确界能够增大，相当于间接增大\mathbf{P}(\mathbf{v})\mathbf{的极大似然}}$

4、代码实现

DBN可以做分类，但本质上还是一个生成模型，本文主要实现图片前向传播再返回来。

来看原始图片

训练之后复原的结果

乍一看还不错是吧，其实，这是训练数据很少的情况下(代码仅用20个数据)

当训练数据变多之后，结果一言难尽了，每张图片出去逛一圈后回来就面目全非，但还是保留了一些特征，仔细还是能够分辨出大致摸样。不过据说用于分类还是不错的，感兴趣的可以去试试。

import numpy as np
from torchvision.datasets import MNIST
np.random.seed(2)
from tqdm import tqdm
import matplotlib.pyplot as plt
class RBM():
    def __init__(self,x_layer,h_layer):
        '''
        :param x_num: 可见层维度
        :param h_num: 隐藏层维度
        '''
        self.x_layer=x_layer #可见层的维度
        self.h_layer=h_layer #隐藏层的维度
        self.w=np.random.normal(0, 0.1, size=(self.x_layer, self.h_layer)) #从正态分布中随机采样w
        self.a=np.random.normal(0, 0.1, size=(self.h_layer,1)) #从正态分布中随机采样a
        self.b=np.random.normal(0, 0.1, size=(self.x_layer,1)) #从正态分布中随机采样b
        self.learning_rate=0.1 #学习率
    def train(self,x,K):
        '''
        :param x: 训练数据
        :param K: 使用k次吉布斯采样
        :return:
        '''
        x_num=x.shape[0] #样本的个数

        for _ in tqdm(np.arange(100),desc="梯度上升"): #梯度上升迭代10000次
            x0=x
            #################
            #CD-K吉布斯采样
            for _ in np.arange(K): #吉布斯采样K次

                P_h=self.sigmoid_Ph_x(x0) #从v0计算出P(h=1|v0)

                #从P(h=1|v0)采样出h0
                h0=np.random.binomial(1,p=P_h,size=(x_num,self.h_layer))
                #计算出P(v|h0)
                P_x=self.sigmoid_Px_h(h0)

                #采样出v
                x0=np.random.binomial(1,p=P_x,size=(x_num,self.x_layer))
            #################
            #真实数据的P(h=1|x)
            true_h =self.sigmoid_Ph_x(x)

            #采样数据的P(h=1|x)
            x_sample_h=self.sigmoid_Ph_x(x0)
            #w梯度
            w_GD=(x.T@true_h-x0.T@x_sample_h)/x_num

            #a梯度
            a_GD=np.mean(true_h-x_sample_h,axis=0).reshape(-1,1)

            #b梯度
            b_GD=np.mean(x-x0,axis=0).reshape(-1,1)

            #梯度下降
            self.w+=self.learning_rate*w_GD
            self.a+=self.learning_rate*a_GD
            self.b+=self.learning_rate*b_GD
    def sigmoid_Ph_x(self,x):
        '''
        计算P(h=1|x)
        :param x: 数据
        :return:
        '''
        H=x @ self.w+self.a.T
        result=1/(1+np.exp(-H))
        return result
    def sigmoid_Px_h(self,h):
        '''
        计算P(x=1|h)
        :param h:
        :return:
        '''
        H=(self.w @ h.T + self.b).T
        result=1/(1+np.exp(-H))
        return result
class DBN():
    def __init__(self,layer):
        '''
        :param layer: 每一层的神经元个数
        '''
        self.layer=layer
        layer_num=len(layer) #计算有多少层
        self.RBMS=[] #储存多个受限玻尔兹曼机
        for i in np.arange(layer_num-1): #迭代初始化多个受限玻尔兹曼机
            rbm=RBM(layer[i],layer[i+1])
            self.RBMS.append(rbm)
    def train(self,data,k):
        '''
        :param data: 训练数据
        :param k:  #CD-k采样次数
        :return:
        '''
        for rbm in self.RBMS: #迭代训练每一个RBM
            rbm.train(data,k) #训练
            p=rbm.sigmoid_Ph_x(data) #计算出下一层的概率
            data=np.random.binomial(1,p,size=p.shape) #根据概率采样
    def predict(self,x):
        #前向传播
        for rbm in self.RBMS:
            p=rbm.sigmoid_Ph_x(x) #计算概率
            x = np.random.binomial(1, p, size=p.shape) #依据概率采样

        #反向传播
        for rbm in reversed(self.RBMS):
            p=rbm.sigmoid_Px_h(x) #计算概率
            x = np.random.binomial(1, p, size=p.shape) #采样
        return x #得到结果
if __name__ == '__main__':
    mnist=MNIST(root="./data/",download=True) #加载数据集
    x=mnist.data.numpy() #转为numpy
    x[x>0]=1 #受限玻尔兹曼机为0，1的二值，所以此处对于大于0的值都转为1
    x=x.reshape(-1,784) #原类型图片为(28,28)，重塑形状
    k=2 #吉布斯采样k次
    x_train=x[:20,:] #取出前20
    x_test=x[:10,:] #测试数据
    dbn=DBN([784,1000,1000]) #初始化，第一层1000神经元，第二场1000，以此类推
    dbn.train(x_train,k) #训练
    result=dbn.predict(x_test) #预测
    result=result.reshape(-1,28,28) #重塑回图片类型
    for i in range(6):
        plt.subplot(2, 3, i+1)
        plt.imshow(result[i])
        plt.gray()
    plt.show()

5、结束

以上，就是DBN的简答介绍和代码实现了。如有问题，还望指出，阿里嘎多。