Dijkstra算法的python实现（算法证明、记录最短路径长度及路径信息）

Dijkstra算法的python实现，能够求解起始节点到各个节点的最短路径长度及路径信息；并且进行了算法有效性证明

紫投

3007人浏览 · 2024-01-09 17:36:04

紫投 · 2024-01-09 17:36:04 发布

Dijkstra算法

一、算法描述及证明

1.1、算法描述及核心思想

Dijkstra算法能够求解无负权图（连通图、有向或无向）的单源最短路径：确定起始节点到所有其他节点的最短路径长度。

Dijkstra算法的基本步骤如下：

创建一个集合 $A$ 保存已经找到最短路径的节点，并初始化为空集（其补集为未确定最短路径的节点）；
创建一个列表 $L$ 保存起始节点到各个节点（包含起始节点）的最短路径长度，并初始化
- 注意起始节点到自身的最短路径长度设为0，到其他节点的最短路径长度设为无穷大（后续编码时使用足够大的正数即可）；
从数组中选择元素值最小（最短路径长度最小）的节点（要求未在集合中），并将其加入到集合 $A$ 中；
对于步骤3中选择的节点的所有未在集合 $A$ 中的相邻节点，进行列表 $L$ （最短路径长度）更新判断
- 如果通过起始节点及步骤3中选择的节点可以找到比当前保存的最短路径长度更小的路径，则更新数组 $L$ 中的元素值
重复步骤3和步骤4，直到所有节点都被加入到集合 $A$ 中；
算法结束后，最终列表 $L$ 中保存的就是源节点到每个节点的最短路径长度。

具体示例可观看该视频：【【算法】最短路径查找—Dijkstra算法】 https://www.bilibili.com/video/BV1zz4y1m7Nq/?share_source=copy_web&vd_source=c71860a35ae6f457f141a44ee4b38133

对于步骤4进行说明：

在这里插入图片描述

图结构说明：起始节点记为 $S$ ，节点 $i$ 的未在集合 $A$ 中的相邻节点为 $j$ 、 $k$ ，路段长度分别为2、9（ $d [i] [j] = 2 、 d [i] [k] = 9$ ）
步骤3确定了起始节点到节点 $i$ 的最短路径长度为3（ $d [S] [i] = 3$ ），此时 $S$ 到节点 $j$ 、 $k$ （节点 $i$ 的相邻节点）的最短路径长度分别为8、10（ $d [S] [j] = 8 、 d [S] [k] = 10$ ）
则步骤4中，进行如下判断:
- 对于节点 $j$ ，因为 $d [S] [j] < d [S] [i] + d [i] [j]$ ，所以更新 $S$ 到节点 $j$ 的最短路径长度为5（列表 $L$ 更新）；
- 对于节点 $k$ ，因为 $d [S] [k] > d [S] [i] + d [i] [k]$ ，所以不更新 $S$ 到节点 $k$ 的最短路径长度（仍然为10）；

步骤4中距离更新的核心公式为： $d [S] [j] = min (d [S] [j], d [S] [i] + d [i] [j])$

Dijkstra算法的核心思想是贪心 + 动态规划 + 广度优先（BFS）

动态规划：维护一个起始节点到各个节点的最短路径长度数组 $L$ ，更新起始节点到集合中节点的最短路径长度；

贪心：从列表 $L$ 中未确定最短路径长度的节点中选择路径长度最短的节点，将该路径长度作为起始节点到该节点的最短路径长度（更新列表 $L$ 中对应的元素值）

广度优先：对于刚刚确定最短路径长度的节点，判断其相邻节点到起始节点的最短路径长度是否应更新

关于Dijkstra算法的核心思想具体讨论可参考该文章：戴克斯特拉算法（Dijkstra）的本质是贪心，还是动态规划？ - Chizhong Jin的回答 - 知乎
https://www.zhihu.com/question/22311234/answer/560996420

1.2、算法有效性证明

Dijkstra算法有效性证明：

命题：从数组中选择元素值最小（最短路径长度最小）的节点，此时的元素值即为起始节点到该节点的最短路径长度

采用数学归纳法证明：

初始状态，步骤3选择的节点为起始节点 $S$ ，步骤4中更新 $S$ 到其相邻节点的最短路径长度，则下一个循环中步骤3所选的节点必然满足命题（图中无负权）；
对于某个循环，步骤3选择的节点为 $i$ ，节点 $S$ 到该节点的距离为 $d [S] [i]$ ，采用反证法证明 $d [S] [i]$ 即为节点 $S 、 i$ 之间的最短路径长度
- 假设 $d [S] [i]$ 不是节点 $S 、 i$ 之间的最短路径长度，则节点 $S 、 i$ 之间一定存在一条最短路径，且路径上至少包含一个未在集合 $A$ 中的节点
- 说明： $S$ 到 $i$ 的路径，若路径上全部节点都在集合 $A$ 中，在之前的循环中已经经由步骤4进行了最短路径长度的更新，即选择节点 $i$ 时的 $d [S] [i]$ 一定是节点 $S 、 i$ 之间的最短路径长度
- 假设路径上只包含一个未在集合 $A$ 中的节点为 $m$ （路径上存在多个未在集合 $A$ 中的节点时可同样证明），则路径 $S - ... - m - i$ 的长度为 $d [S] [m] + d [m] [i]$ ，因为步骤3选择了节点 $i$ 而不是节点 $m$ ，因此 $d [S] [m] >= d [S] [i]$ ，则 $d [S] [m] + d [m] [i] >= d [S] [i]$ （无负权 $d [m] [i] >= 0$ ），与假设矛盾，证明完毕

在这里插入图片描述

详细的证明可参考该文章：【网络流优化(三)】最短路问题(Shortest Path Problem)与Dijkstra’s算法（附Python代码实现） - 王源的文章 - 知乎
https://zhuanlan.zhihu.com/p/374725969

1.3、确定最短路径信息

Dijkstra算法使用列表 $L$ 记录起始节点到各个节点的最短路径长度，如果需要确定最短路径上的节点编号，则需要额外记录每个节点的“上游节点”

能够确定最短路径信息的Dijkstra算法的基本步骤如下：

创建一个集合 $A$ 保存已经找到最短路径的节点，并初始化为空集；
创建一个列表 $L$ 保存起始节点到各个节点（包含起始节点）的最短路径长度，并初始化
- 注意起始节点到自身的最短路径长度设为0，到其他节点的最短路径长度设为无穷大（后续编码时使用足够大的正数即可）；
创建一个字典 $D$ 保存节点的“上游节点”，形如{节点编号：上游节点编号}，初始化为空字典；
从数组中选择元素值最小（最短路径长度最小）的节点（要求未在集合中），并将其加入到集合 $A$ 中；
对于步骤4中选择的节点的所有未在集合 $A$ 中的相邻节点，进行列表 $L$ （最短路径长度）更新判断
- 如果通过起始节点及步骤4中选择的节点可以找到比当前保存的最短路径长度更小的路径，则更新数组 $L$ 中的元素值，字典 $D$ 中的信息也需要同步更新
重复步骤4和步骤5，直到所有节点都被加入到集合 $A$ 中；
算法结束后，最终列表 $L$ 中保存的就是源节点到每个节点的最短路径长度；
根据字典 $D$ 中的信息可以确定每个起始节点到各个节点的最短路径信息（路径上的节点编号）
- 根据节点编号（key值）确定“上游节点”（value值），继续回溯“上游节点”的“上游节点”直至起始节点（递归求解）

二、示例代码

2.1、求解最短路径长度

使用邻接矩阵记录节点之间的邻接关系

$a_{ij}$ 表示节点 $i 、 j$ 是否相连，不相连则 $a_{ij}=0$ （ $i = j$ 时， $a_{ij}=0$ ），否则 $a_{ij}=1$ （如果是加权图，则为权重值）
$\begin{equation} a_{ij}=\left\{ \begin{aligned} 1 & \quad i,j相邻\\ 0 & \quad i,j不相邻\\ \end{aligned} \right . \end{equation}$

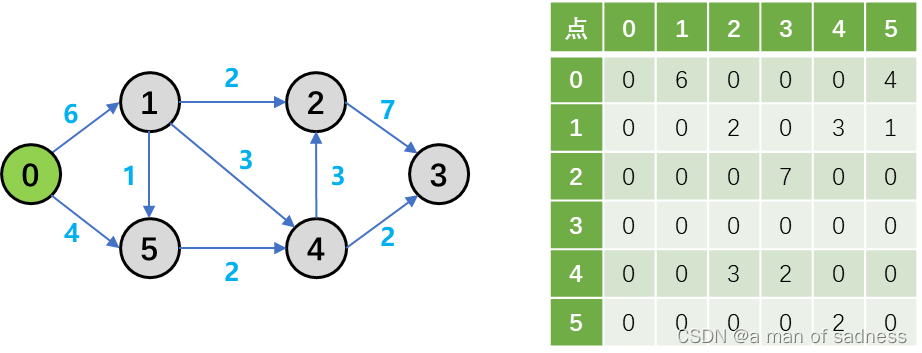
import numpy as np


node_num = 6
adjacent_matrix = np.zeros((node_num, node_num))

# 邻接矩阵
adjacent_matrix[0, 1] = 6
adjacent_matrix[0, 5] = 4
adjacent_matrix[1, 2] = 2
adjacent_matrix[1, 4] = 3
adjacent_matrix[1, 5] = 1
adjacent_matrix[2, 3] = 7
adjacent_matrix[4, 2] = 3
adjacent_matrix[4, 3] = 2
adjacent_matrix[5, 4] = 2

在这里插入图片描述

使用优先队列记录未确定最短路径长度的节点（功能类似于集合 $A$ 的补集）

往优先队列中添加元素需要给出该元素的排序对象（节点）、排序依据（起始节点到该节点的最短路径长度–暂时）
优先队列能够方便地从未确定最短路径长度的节点中选出最短路径长度最小的节点

import queue


# 使用优先队列（能够方便地获取距离start_node最近的节点）
priority_queue_instance = queue.PriorityQueue(node_num)

# 添加节点，以start_node为例（start_node到节点的距离为排序依据）
priority_queue_instance.put((0, self.start_node))

# 获取节点（路径长度、节点）
length, temp_node = priority_queue_instance.get()

使用优先队列的Dijkstra算法的基本步骤如下（仅列出关键步骤，详见代码）：

创建一个空的优先队列，用于选择节点；
将起始节点加入优先队列，其最短路径长度为0；
循环执行以下步骤，直到优先队列为空：
- 从优先队列中选择（弹出）最短路径长度最小的节点，将其标记为已访问；
- 遍历当前节点的所有邻居节点（且未确定最短路径长度）：
  - 更新起始节点到这些节点的最短路径长度路径： $d [S] [j] = min (d [S] [j], d [S] [i] + d [i] [j])$ ；
  - 当 $d [S] [i] + d [i] [j] < d [S] [j]$ 时，记录或更新节点的“上游节点”；
  - 将这些节点添加（压入）进优先队列（节点 + 更新后的路径长度）

import numpy as np
import queue


start_node = 0
node_num = 6
adjacent_matrix = np.zeros((node_num, node_num))
path_maximum = 1000	#足够大的正数

# 记录各个节点到start_node的路径长度（包含start_node），start_node到start_node的长度为0，start_node到其余节点的长度取path_maximum
path_length = [self.path_maximum] * self.node_num

# 记录各个节点是否被标记
detect_flag = [False] * self.node_num

# 使用字典记录上游节点（不包含start_node），用于确定start_node到各个节点的路径
up_node_info = {}

# 使用优先队列（能够方便地获取距离start_node最近的节点）
priority_queue_instance = queue.PriorityQueue(node_num)

# 添加start_node，以start_node到节点的距离为排序依据
priority_queue_instance.put((0, start_node))

# 队列非空时（start_node到各个节点的最短距离未完全确定）
while not priority_queue_instance.empty():
    length, temp_node = priority_queue_instance.get()
    # 更新起点至节点的距离、标记节点
    path_length[temp_node] = length
    detect_flag[temp_node] = True
    # 确定节点之后更新起点至temp_node相邻且未访问节点的距离
    for i in range(node_num):
        if adjacent_matrix[temp_node][i] > 0 and not detect_flag[i]:
            # 更新up_node_info
            if path_length[temp_node] + adjacent_matrix[temp_node][i] < path_length[i]:
                up_node_info[i] = temp_node

            # 距离更新d[s][i]=min(d[s][i], d[s][temp]+d[temp][i])
            path_length[i] = min(path_length[i], path_length[temp_node] + adjacent_matrix[temp_node][i])
            # 优先队列更新
            priority_queue_instance.put((path_length[i], i))

# 确定最短路径信息
# path_info = get_shortest_path()

在这里插入图片描述

2.2、确定最短路径信息

在确定各个节点的“上游节点”之后，可根据该信息确定最短路径信息

def get_shortest_path(up_node_info, start_node, node_num):
    """
    确定start_node到其他节点的最短路径
    :param up_node_info: 节点的上游节点信息
    :param start_node: 起始节点
    :param start_node: 节点个数
    :return:
    """
    # 记录start_node到各个节点的最短路径
    path_info = {}
    for i in range(self.node_num):
        if i != self.start_node:
            path = []
            # 递归确定节点上游的各个节点（直至start_node）
            path_info[i] = get_path_process(up_node_info, start_node, i, path)
	
    return path_info


def get_path_process(up_node_info, start_node, end_node, path):
    """
    递归确定end_node上游的各个节点（直至start_node）
    :param up_node_info: 节点的上游节点信息
    :param start_node: 起始节点
    :param end_node: 末端节点
    :param path: 最短路
    :return: 最短路
    """
    up_node = up_node_info[end_node]
    if up_node == start_node:
        path.insert(0, end_node)
        path.insert(0, start_node)
        return path
    else:
        path.insert(0, end_node)
        get_path_process(up_node, path)
        return path