Numpy数组的切片和索引

一、一维数组的切片和索引

冒号分割切片参数[start:stop:step]

• ndarray对象的内容可以通过索引或切片来访问和修改，与Python中list的切片操作一样。
• ndarray数组可以基于0-n的下标进行索引

注意：区别在于数组切片是原始数组视图（这就意味着，如果做任何修改，原始数组都会跟着更改）。这也意味着，如果不想更改原始数组，我们需要进行显式的复制，从而得到它的副本(.copy())。

通过切片和copy复制原列表都是复制赋值，通过直接等于是引用赋值。

冒号:的解释：如果只放置一个参数，

• 如[2]，将返回与该索引相对应的单个元素
• 如果为[2:],表示从该索引开始以后所有的项都将被提取
• 如果使用了两个参数，如[2:7]，那么则提取两个索引（不包括停止索引）之间的项

为什么切片和区间会忽略最后一个元素
计算机科学家edsger w.dijkstra(艾兹格.W.迪科斯彻)，delattr这一风格的解释应该是比较好的：

• 当只有最后一个位置的信息时（比如最后一个位置的下标为3），我们可以快速看出切片和区间里有几个元素：range(3)和my_list[:3]
• 当起始位置信息都可见时，我们可以快速计算出切片和区间的长度，用有一个数减去第一个下标(stop-start)即可
• 这样做也可以让我们利用任意一个下标把序列分割成不重叠的两部分，只要写成my_list[:x]和my_list[x:]即可。

比如：

ar = np.array([10,20,30,40,50,60])
# 在下标2的地方开始切割
print('ar[2:]',ar[2:])
# 在下标3的之前结束分割
print('ar[:3]',ar[:3])
# 使用下标2将数组分割成不重叠的两部分
print('ar[:2]',ar[:2])
print('ar[2:]',ar[2:])

输出结果：

二、二维数组的切片和索引

同样适用上述索引提取方法。

注意：切片还可以使用省略号"……"，如果在行位置使用省略号，那么返回值将包含所有行元素；反之，则包含所有列元素。

三、索引的高级操作

3.1 整数数组索引

在numpy中还可以使用高级索引方式，比如整数数组索引、布尔索引，以下将对两种索引介绍。

# 创建二维数组
x = np.array([
    [1,2],
    [2,4],
    [5,6]
])
# [0,1,2]代表行索引；[0,1,0]代表列索引
y = x[[0,1,2],[0,1,0]]
# y分别获取x中的(0,0)、(1,1)和(2,0)的数据
y

结果是：

• 获取了4*3数组中四个角上元素，它们对应的行索引是[0,0]和[3,3]，列索引是[0,2]和[0,2].

b = np.array([
    [0,1,2],
    [3,4,5],
    [6,7,8],
    [9,10,11]
])
a = b[[0,0,3,3],[0,2,0,2]]
print('a:',a)
r = np.array([[0,0],[3,3]]).reshape(4)
print('r:',r)
l = np.array([[0,2],[0,2]]).reshape(4)
print('l:',l)
s = b[r,l].reshape((2,2))
print('s:',s)

输出结果是：

等同于：

a = b[[0,0,3,3],[0,2,0,2]].reshape((2,2))
a

• 练习
  创建一个8*8的国际象棋棋盘矩阵（黑块为0，白块为1）：
  1.[0 1 0 1 0 1 0 1]
  2.[1 0 1 0 1 0 1 0]
  3.[0 1 0 1 0 1 0 1]
  4.[1 0 1 0 1 0 1 0]
  5.[0 1 0 1 0 1 0 1]
  6.[1 0 1 0 1 0 1 0]
  7.[0 1 0 1 0 1 0 1]
  8.[1 0 1 0 1 0 1 0]

​第一步：

# 先创建一个全0数组
Z = np.zeros((8,8),dtype=int)
Z

输出结果：

第二步：

# 将其中一部分元素的值改为1
Z[1::2,::2] = 1
Z

输出结果：

第三步：

# 再将剩下的部分元素变为1
Z[::2,1::2] = 1
Z

输出结果：

3.2 布尔数组索引

当输出结果需要经过布尔运算(如比较运算)时，此时会使用到另一种高级索引方式，即布尔数组索引。下面示例返回数组中大于6的所有元素：

# 返回所有大于6的数字组成的数组
x = np.array([[0,1,2],[3,4,5],[6,7,8],[9,10,11]])
x[x>6]

• 布尔索引实现的是通过一维数组中的每个元素的布尔型数值对一个与一维数组有着同样行数或列数的矩阵进行符合匹配。这种作用，其实是把一维数组中布尔值为True的相应行或列给抽取出来。
• 注意：一维数组的长度必须和想要切片的维度或轴的长度一致。

练习：
1.提取出数组中所有奇数
2.修改奇数值为-1

筛选出指定区间内数据：

1. &和
2. | 或

True和False的形式表示需要和不需要的数据

也可以用两个一维布尔数组进行切片

从上面的结果可以知道，能够进行切片的前提是：两个一维布尔数组中True的个数需要相等。
如果索引形状不匹配，则索引数组无法与该形状一起广播。当访问numpy多维数组时，用于索引的数组需要具有相同的形状(行和列)。numpy将有可能去广播，所以，若要为了实现不同维度的选择，可分两步对数组进行选择。

1. 例如我需要选择第一行和最后一行的第1,3,4列时，先选择行，再选择列
2. 选读取数组a3_4的第一行和最后一行，保存到temp，然后再筛选相应的列即可。

3.3 数组索引及切片的值更改会修改原数组

ar = np.arange(10)
print(ar)
ar[5] = 100
ar[7:9] = 200
print(ar)
# 一个标量赋值给一个索引/切片时，会自动改变/传播原始数组

输出结果：

• 可以使用复制操作

# 复制
ar = np.arange(10)
b = ar.copy()
# 或者b=np.array(ar)
b[7:9] = 200
print('ar:',ar)
print('b:',b)

输出结果是：

四、numpy广播机制

4.1 numpy的广播机制

广播（Broadcast）是numpy对不同形状（shape）的数组进行数值计算的方式，对数组的算术运算通常在相应的元素上进行。
如果两个数组a和b形状相同，即满足a.shape == b.shape，那么a*b的结果就是a与b数组对应位相乘。这要求维数相同，且各维度的长度相同。

但如果是两个形状不同的数组呢？它们之间就不能进行运算吗？当然不是，为了保持数组形状相同，Numpy设计了一种广播机制，这种机制的核心是对形状较小的数组，在横向或纵向上进行一定次数的重复，使其与形状较大的数组拥有相同的维度。

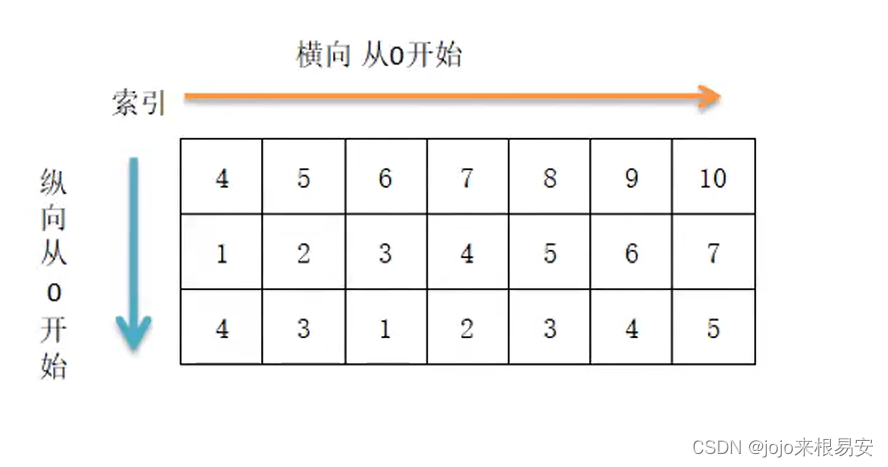
下面的图片展示了数组b如何通过广播来与数组a兼容：

4*3的二维数组与长为3的一维数组相加，等效于把数组b在二维上重复4次再运算。

4.2广播的规则

• 让所有输入数组都向其中形状最长的数组看齐，形状中不足的部分通过在前面加1补齐。
• 输出数组的形状是输入数组形状的各个维度上的最大值。
• 如果输入数组的某个维度和输出数组的对应维度的长度相同或者其长度为1，这个数组能够用来计算，否则出错。
• 当输入数组的某个维度的长度为1时，沿着此维度运算时都用此维度上的第一组值。

M = np.ones((2,3))
print(M)
a = np.arange(3)
print(a)
# 两个数组的形状为 M.shape(2,3)，a.shape=(3,)
# 可以看到，根据规则1，数组a的维度更小，所以在其左边补1，变成M.shape -> (2,3) , a.shape -> (1,3)
# 根据规则2，第一个维度不匹配，因此扩展这个维度以匹配数组：M.shape -> (2,3) , a.shape -> (2,3)
# 现在这两个数组的形状匹配了，可以看到它们的最终形状都为(2,3)
M + a

输出结果：

a = np.arange(3).reshape((3,1))
print('a:',a)
b = np.arange(3)
print('b:',b)
a+b

# 两个数组的形状为：a.shape(3,1),b.shape(3,)
# 根据规则1，需要用1将b的形状补全：a.shape -> (3,1) , b.shape -> (1,3)
# 根据规则2，需要更新两个数组的维度来相互匹配：a.shape -> (3,3) , b.shape -> (3,3)
# 因为结果匹配，所以两个形状是兼容的

输出结果：

4.3 对广播规则另一种简单理解

• 将两个数组的维度大小右对齐，然后比较对应维度上的数值
• 如果数值相等或者其中有一个为1或者为空，则能进行广播运算
• 输出的维度大小为取数值打的数值。否则不能进行数组运算。

右对齐1：

数组a的大小为(2,3)
数组b的大小为(1,)
首先右对齐：
    2  3
       1
------------
    2  3 
所以最后两个数组运算的输出大小为：(2,3)

示例：

# 数组a的大小为(2,3)
a = np.arange(6).reshape(2,3)
print('a:',a)
# 数组b的大小为(1,)
b = np.array([5])
print('b:',b)
c = a*b
# 输出的大小为(2,3)
c

输出结果：

右对齐2：

数组a大小为(2,1,3)
数组b大小为(4,1)
首先右对齐：
  2  1  3
     4  1
----------
  2  4  3
所以最后两个数组运算的输出大小为(2,4,3)

示例：

# 数组大小为(2,1,3)
a = np.arange(6).reshape(2,1,3)
print('a:',a)
print('--'*10)
# 数组大小为(4,1)
b = np.arange(4).reshape(4,1)
print('b:',b)
print('--'*10)
c = a + b
print(c,c.shape)

输出结果：

从这里能够看出：

• 两个数组右对齐以后，对应维度里的数值要么相等，要么为1，要么缺失取大值
• 除此之外就会报错，像下面的两个数组就不能做运算

不能匹配的例子：

数组a的大小为(2,1,3)
数组b的大小为(4,2)
首先右对齐：
  2  1  3
     4  2
-----------
2和3不匹配，此时就不能做运算，除非将2换成1或者3才能向匹配

示例：

# 数组a大小为(2,1,3)
a = np.arange(6).reshape(2,1,3)
print('a:',a)
print('--'*10)
# 数组b的大小为(4,2)
b = np.arange(8).reshape(4,2)
print('b:',b)
print('--'*10)
# 运行报错
a + b  

输出结果：

总结