5. 广义视角下的 GNN 框架

• GNN 层的本质为：消息（Message） + 聚合（Aggregation）。在这一视角下的有许多不同的实例：GCN，GraphSAGE，GAT等，下面我们将着重讲解这三个不同的实例。

GNN 的总体框架分别包括：1）消息 与 2）聚合，也就是一个网络层中的操作。

3）层与层之间的连接

4）图增广（Graph augmentation） 与 5）学习目标（Learning Object）

下面我们一部分一部分进行分析。

---

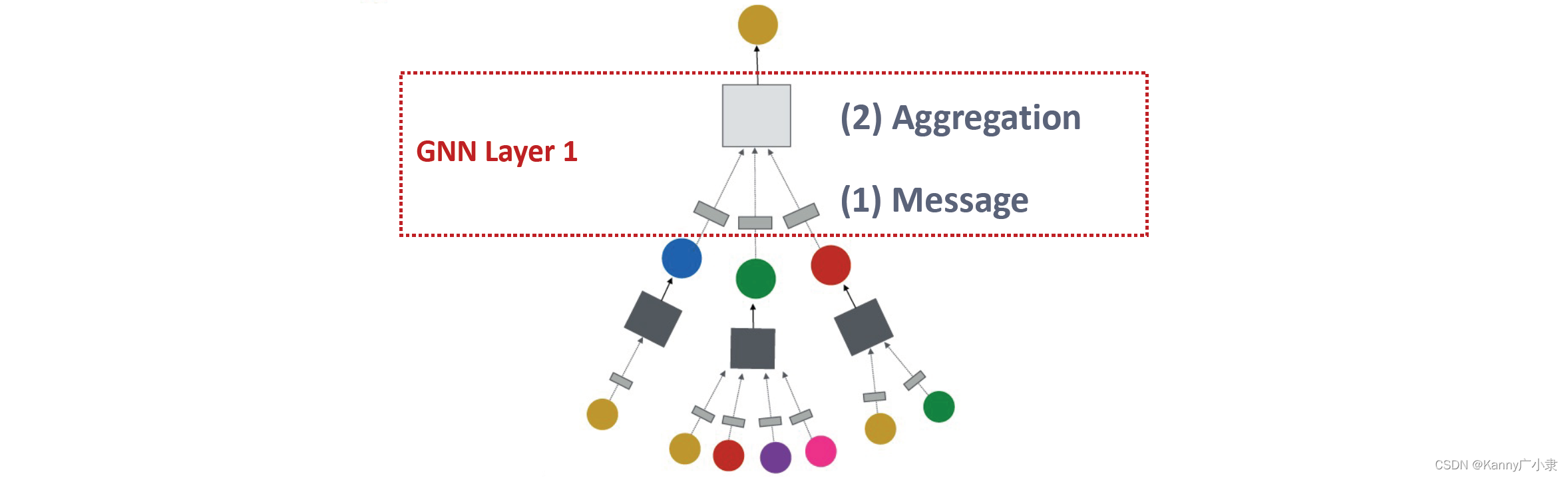
1）消息（Message）

图网络中的message函数可以通过下式进行表示：

$${\mathbf{m}}_u^{(l)}={\mathrm{MSG}}^{(l)}\left({\mathbf{h}}_u^{(l-1)}\right)$$

主要想法是：每个节点将创建一条消息，稍后再发送给其他节点。

最简单的message函数是线性变换：

$${\mathbf{m}}_u^{(l)}={\mathbf{W}}^{(l)}{\mathbf{h}}_u^{(l-1)}$$

其通过将节点特征 ${\mathbf{h}}_u^{(l-1)}$ 乘以权重矩阵 ${\mathbf{W}}^{(l)}$，得到变换之后的message。

---

2）聚合（Aggregation）

每个节点，假设当前节点为$v$都将从其邻居节点$N(v)$中聚合信息

$${\mathbf{h}}_v^{(l)}={\mathrm{A}\mathrm{G}\mathrm{G}}^{(l)}\left(\left\{{\mathbf{m}}_u^{(l)},u\in N(v)\right\}\right)$$

聚合函数可以选取：求和 $\mathrm{Sum}(\cdot )$, $\mathrm{Mean}(\cdot )$ 或 $\mathrm{Max}(\cdot )$ 函数。

但这样直接聚合邻居节点会有一个问题：自身节点本身的信息会被遗失。
因此，在聚合操作时，我们考虑自身信息与邻居信息，首先分别进行一次变换，转为对应的message。

而后再通过拼接（Concatenation）的方式来将自身节点与邻居节点汇总的信息进行聚合。

$${\mathbf{h}}_v^{(l)}=\mathrm{CONCAT}\left(\mathrm{AGG}\left(\left\{{\mathbf{m}}_u^{(l)},u\in N(v)\right\}\right),{\mathbf{m}}_v^{(i)}\right)$$

在经过了聚合之后通常需要再进行一次非线性激活层 $\sigma (\cdot )$，通常为：$\mathrm{ReLU}(\cdot ),\mathrm{Sigmoid}(\cdot ),\cdots$

后面以这种广义视角，分别单独介绍三种网络中的信息与聚合结构。