CSP-J(入门级)2024年T3 小木棍
小 S 喜欢收集小木棍。在收集了n根长度相等的小木棍之后,他闲来无事,便用它们拼起了数字。用小木棍拼每种数字的方法如下图所示。现在小 S 希望拼出一个n0小 S 想知道这个数是多少,可n很大,把木棍整理清楚就把小 S 折腾坏了,所以你需要帮他解决这个问题。如果不存在正整数满足以上条件,你需要输出−1进行报告。
[CSP-J 2024] 小木棍(民间数据)
题目描述
小 S 喜欢收集小木棍。在收集了 n n n 根长度相等的小木棍之后,他闲来无事,便用它们拼起了数字。用小木棍拼每种数字的方法如下图所示。
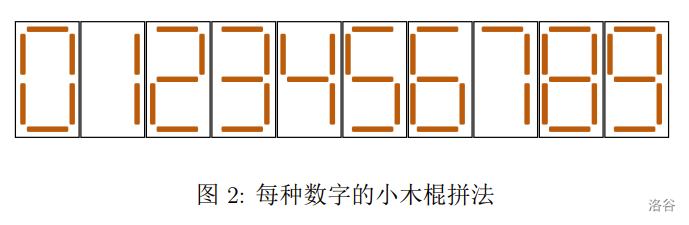
现在小 S 希望拼出一个正整数,满足如下条件:
- 拼出这个数恰好使用 n n n 根小木棍;
- 拼出的数没有前导 0 0 0;
- 在满足以上两个条件的前提下,这个数尽可能小。
小 S 想知道这个数是多少,可 n n n 很大,把木棍整理清楚就把小 S 折腾坏了,所以你需要帮他解决这个问题。如果不存在正整数满足以上条件,你需要输出 − 1 -1 −1 进行报告。
输入格式
本题有多组测试数据。
输入的第一行包含一个正整数 T T T,表示数据组数。
接下来包含 T T T 组数据,每组数据的格式如下:
一行包含一个整数 n n n,表示木棍数。
输出格式
对于每组数据:输出一行,如果存在满足题意的正整数,输出这个数;否则输出 − 1 -1 −1。
样例 #1
样例输入 #1
5
1
2
3
6
18
样例输出 #1
-1
1
7
6
208
提示
【样例 1 解释】
- 对于第一组测试数据,不存在任何一个正整数可以使用恰好一根小木棍摆出,故输出 − 1 -1 −1。
- 对于第四组测试数据,注意 0 0 0 并不是一个满足要求的方案。摆出 9 9 9、 41 41 41 以及 111 111 111 都恰好需要 6 6 6 根小木棍,但它们不是摆出的数最小的方案。
- 对于第五组测试数据,摆出 208 208 208 需要 5 + 6 + 7 = 18 5 + 6 + 7 = 18 5+6+7=18 根小木棍。可以证明摆出任何一个小于 208 208 208 的正整数需要的小木棍数都不是 18 18 18。注意尽管拼出 006 006 006 也需要 18 18 18 根小木棍,但因为这个数有前导零,因此并不是一个满足要求的方案。
【数据范围】
对于所有测试数据,保证: 1 ≤ T ≤ 50 1 \leq T \leq 50 1≤T≤50, 1 ≤ n ≤ 1 0 5 1 \leq n \leq 10^5 1≤n≤105。
| 测试点编号 | n ≤ n\leq n≤ | 特殊性质 |
|---|---|---|
| 1 1 1 | 20 20 20 | 无 |
| 2 2 2 | 50 50 50 | 无 |
| 3 3 3 | 1 0 3 10^3 103 | A |
| 4 , 5 4,5 4,5 | 1 0 5 10^5 105 | A |
| 6 6 6 | 1 0 3 10^3 103 | B |
| 7 , 8 7,8 7,8 | 1 0 5 10^5 105 | B |
| 9 9 9 | 1 0 3 10^3 103 | 无 |
| 10 10 10 | 1 0 5 10^5 105 | 无 |
特殊性质 A:保证 n n n 是 7 7 7 的倍数且 n ≥ 100 n \geq 100 n≥100。
特殊性质 B:保证存在整数 k k k 使得 n = 7 k + 1 n = 7k + 1 n=7k+1,且 n ≥ 100 n \geq 100 n≥100。
【解析】
先说暴力解,这道题乍一看没什么思路,在考试中遇到这样的情况可以先写个暴力解,这道题有两种暴力解的思路:
【思路一,枚举】可以枚举每个数,看它由几根小木棍组成,最先出现的木棍个数即为答案,详见代码:
#include <bits/stdc++.h>
using namespace std;
int t, n;
int a[10] = {6, 2, 5, 5, 4, 5, 6, 3, 7, 6}; //a[i]表示数字i由几根小木棍构成
int ans[10000005];
int main() {
for(int i = 1; i <= 1e7; i++) { //枚举每个数字
int sum = 0; //小木棍个数
int t = i;
while(t > 0) { //循环计算每一位的小木棍个数
sum += a[t % 10]; //求和
t /= 10;
}
if (ans[sum] == 0) { //如果是第一次出现
ans[sum] = i; //即为答案
}
}
cin >> t;
while(t--) {
cin >> n;
if (ans[n] == 0) ans[n] = -1; //没有答案,变成-1
cout << ans[n] << "\n";
}
return 0;
}
【思路二,搜索】代码略:
第二步可以分析特殊性质:
【特殊性质A】n是7的倍数且n>=100,
由于单个数字最多由7根小木棍组成数字8,而位数越少,数越小,所以n为7的倍数且大于等于100,由n/7个8组成的数字最小。
【特殊性质B】n是7的倍数多1,且n>=100,则可以确定是有10开头,后边(n-1-7)/7个8。
特殊性质AB可以解决3,4,5,6,7,8这6个测试点,详见代码:
#include <bits/stdc++.h>
using namespace std;
int t, n;
int main() {
cin >> t;
while(t--) {
cin >> n;
if (n % 7 == 0) {
for(int i = 1; i <= n / 7; i++) {
cout << 8;
}
cout << "\n";
} else if (n % 7 == 1) {
cout << 10;
for(int i = 1; i <= (n - 8) / 7; i++) {
cout << 8;
}
cout << "\n";
}
}
return 0;
}
这样结合打表道姓前50,可以解决8个测试点了。
【正解】
结合前50的打表答案,可以分析出答案是有规律的,而且根据n%7的余数相关,详见代码:
#include <bits/stdc++.h>
using namespace std;
int t, n;
int ans[22] = { 0, -1, 1, 7, 4, 2, 6, 8, 10, 18, 22, 20, 28, 68, 88, 108, 188, 200, 208, 288, 688, 888};
int main() {
cin >> t;
while(t--) {
cin >> n;
if (n <= 21) {
cout << ans[n] << "\n";
} else {
int cnt;
if (n % 7 == 0) {
cnt = n / 7;
} else if (n % 7 == 1) {
cout << 10;
cnt = (n - 8) / 7;
} else if (n % 7 == 2) {
cout << 1;
cnt = (n - 2) / 7;
} else if (n % 7 == 3) {
cout << 200;
cnt = (n - 17) / 7;
} else if (n % 7 == 4) {
cout << 20;
cnt = (n - 11) / 7;
} else if (n % 7 == 5) {
cout << 2;
cnt = (n - 5) / 7;
} else if (n % 7 == 6) {
cout << 6;
cnt = (n - 6) / 7;
}
for(int i=1;i<=cnt;i++){
cout<<8;
}
cout<<"\n";
}
}
return 0;
}

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献14条内容
已为社区贡献14条内容





所有评论(0)