内容概括：

  • 利用基于对话框的MFC项目
  • 实现鼠标点击绘制多边形
  • 实现扫描线算法填充多边形

源码见Yushan-Ji/ComputerGraphics: ECNU2023秋 计算机图形学课程实验代码 (github.com)

实验内容

  1. 通过鼠标交互输入多边形
  2. 对各种多边形进行填充，包括边界自交的情况

算法描述

多边形绘制

  1. 利用OnLButtonDown和OnRButtonDown函数，实现：
    • 左键点击：开始绘制多边形，并连接上一个顶点和当前点击的顶点
    • 右键点击：结束绘制多边形，并连接上一个顶点和第一个顶点
      其中，绘制顶点间的连线利用了MoveTo和LineTo函数
  2. 另外，为了避免多边形绘制完毕后，程序仍然对鼠标点击事件进行响应，因此需要添加布尔变量IsCompleted，用来监测当前多边形是否绘制完毕
    因此在OnLButtonDown和OnRButtonDown函数的最开始，需要添加一个条件判断语句，若IsCompleted为TRUE，则表明多边形已绘制完毕，函数直接返回
  3. 将所有顶点信息保存在vector<CPoint> points中，便于后续计算边信息

扫描线填充
y++\n清空scanPoints
获取边表
AET更新
获取当前扫描线\n的所有交点
交点排序
填充当前扫描线
  1. 首先需要根据points中存储的多边形顶点信息，计算出多边形的边信息，得到ET表
    • 新建Edge类，存储每条边的信息
          // 边信息
    class Edge 
    {
    public:
    	float x_lower; // 扫描线与边的交点x值（初始值为线段下端点x值）
    	float dx; // 斜率倒数
    	float y_upper; // 线段上端点y值
    	// 构造函数
    	Edge() : x_lower(0.0), dx(0.0), y_upper(0.0) {}
    	Edge(float x_val, float dx_val, float y_val);
    };
    • 新建ET表：map<int, vector<Edge>> ET
      • 建立从线段下端点y值y_lower到多边形所有边vector<Edge>的映射，这样有相同下端点的不同边就能够存储在相同键值的map中，便于后续向AET中添加活性边
    • 获取ET表：通过getET()函数实现
      • 需要判断当前边是否为首尾顶点连成的边
      • 计算当前边斜率的倒数dx
        • 若当前边平行于x轴，continue不执行任何操作
        • 若当前边平行于y轴，则dx=0
        • 不是上述两种情况则正常计算
      • 计算x_lower 和y_upper
  2. 初始化、更新AET表
    • 扫描线y初始化为ymin，并将ET表中ymin对应的所有边都添加到AET中
    • 对于每一条扫描线，都需要检查AET中是否有非活性边的存在，还要及时添加新的活性边
      • 当y >= y_upper 时，说明该边需要移除
      • 当y >= y_lower时，说明该边需要添加到AET中
  3. 获取每条扫描线与活性边的交点，存入scanPoints中
    • 对于不同边相交的顶点，不存入
    • 对于其他交点，易知交点数量必为偶数，因此成对存入交点
  4. 根据scanPoints中交点的x值升序排列所有交点，并进行填充

核心代码

CPolygonFillDlg类中新添加的public成员：

class CPolygonFillDlg : public CDialogEx
{
  public:
	std::vector<CPoint> points; // 存储多边形的顶点
	std::vector<CPoint> scanPoints; // 存储扫描线与活动边的交点
    
	BOOL IsCompleted; // 标志多边形是否绘制完毕
    
	std::map<int, std::vector<Edge>> ET; // ET表：从线段下端点y值到边信息链表的映射
	std::vector<Edge> AET; // 活动边表
	float YMAX; // 存储多边形最高点
    
	void getET();
	void PolygonFill();
	static bool compareCPoint(const CPoint& a, const CPoint& b);
}

消息函数

在PolygonFillDlg.cpp中需要添加按钮点击、鼠标点击的消息关联函数

// 消息关联
BEGIN_MESSAGE_MAP(CPolygonFillDlg, CDialogEx)
	...
	ON_WM_LBUTTONDOWN() // 关联鼠标左键点击事件
	ON_WM_RBUTTONDOWN() // 关联鼠标右键点击事件
	ON_BN_CLICKED(IDC_BUTTON_FILL, &PolygonFill) // 关联按钮点击事件
END_MESSAGE_MAP()

在PolygonFillDlg.h中需要添加鼠标点击函数的声明

class CPolygonFillDlg : public CDialogEx
{
    ...
  protected:
    ...
    afx_msg void OnLButtonDown(UINT nFlags, CPoint point);
    afx_msg void OnRButtonDown(UINT nFlags, CPoint point);
    ...
}

多边形绘制

// 鼠标左键点击事件（绘制多边形）
void CPolygonFillDlg::OnLButtonDown(UINT nFlags, CPoint point) 
{
	// 若多边形绘制完毕，忽略该函数，不执行操作
	if (IsCompleted == TRUE) 
	{
		return;
	}
	else 
	{
		// 如果是第一个点，存入points数组中
		if (points.empty()) 
		{
			points.push_back(point);
		}
		// 若不是第一个点，则连接当前点和上一个点
		else 
		{
			CStatic* CANVAS = (CStatic*)GetDlgItem(IDC_STATIC_CANVAS);
			CDC* pDC = CANVAS->GetDC();

			// 获取points数组的最后一个point（就是上一个点），并将当前绘图位置移动到该点
			pDC->MoveTo(points[points.size() - 1]);
			// 连接上一个点和当前点
			pDC->LineTo(point);
			points.push_back(point); // 将当前点加入数组
			ReleaseDC(pDC);
		}
	}
}

// 鼠标右键点击事件（多边形绘制完毕）
void CPolygonFillDlg::OnRButtonDown(UINT nFlags, CPoint point) 
{
	if(IsCompleted == TRUE) 
	{
		return;
	}

	else 
	{
		// 如果前面少于3个点，则无法连接成为多边形，弹出错误信息
		if (points.size() < 3) {
			CString message = _T("顶点数量少于3，无法绘制多边形");
			CString caption = _T("多边形绘制错误");
			MessageBox(message, caption, MB_ICONERROR);
		}

		// 若points已存储有2个以上的顶点，则连接上一个点和第一个点
		else 
		{
			CStatic* CANVAS = (CStatic*)GetDlgItem(IDC_STATIC_CANVAS);
			CDC* pDC = CANVAS->GetDC();
			// 连接第一个点和当前点
			pDC->MoveTo(points[points.size() - 1]);
			pDC->LineTo(points[0]);
			ReleaseDC(pDC);

			// 成功消息
			CString message = _T("多边形绘制完毕");
			CString caption = _T("多边形绘制完毕");
			MessageBox(message, caption, MB_OK);

			IsCompleted = TRUE;
		}
	}
}

扫描线填充

由于扫描线填充涉及到的代码较长，这里不全部展示，仅列出关键的几个步骤

获取边表

void CPolygonFillDlg::getET() 
{
	for (int i = 1; i <= points.size() ; i++) 
	{
		float dx;
		float x_lower, y_lower, y_upper;

		// points中最后一个点和第一个点的连线
		if (i == points.size())
		{
			if (points[i - 1].x == points[0].x)
			{
				continue; // 边平行于x轴，不处理
			}
			else if (points[i - 1].y == points[0].y)
			{
				dx = 0.0;
			}
			else
			{
				dx = (points[i - 1].x - points[0].x) * 1.0 / (points[i - 1].y - points[0].y);
			}

			if (points[0].y <= points[i - 1].y)
			{
				y_lower = points[0].y;
				y_upper = points[i - 1].y;
				x_lower = points[0].x;
			}
			else
			{
				y_lower = points[i - 1].y;
				y_upper = points[0].y;
				x_lower = points[i - 1].x;
			}
			// 插入到Edge边信息中
			Edge e(x_lower, dx, y_upper);
			// 插入到ET表中
			ET[y_lower].push_back(e);
		}

		else 
		{
			// 斜率
			if (points[i - 1].x == points[i].x)
			{
				continue; // 边平行于x轴，不处理
			}
			else if (points[i - 1].y == points[i].y)
			{
				dx = 0;
			}
			else
			{
				dx = (points[i - 1].x - points[i].x) * 1.0 / (points[i - 1].y - points[i].y);
			}

			// 线段上端点的x，y值
			if (points[i - 1].y <= points[i].y)
			{
				y_lower = points[i - 1].y;
				y_upper = points[i].y;
				x_lower = points[i - 1].x;
			}
			else
			{
				y_lower = points[i].y;
				y_upper = points[i - 1].y;
				x_lower = points[i].x;
			}

			// 计算多边形的最高点y值
			if (y_upper >= YMAX)
			{
				YMAX = y_upper;
			}

			// 插入到Edge边信息中
			Edge e(x_lower, dx, y_upper);
			// 插入到ET表中
			ET[y_lower].push_back(e);
		}
	}
}

AET表更新

// 移除已经超出扫描线的边
std::vector<Edge> newAET;
for (auto it = AET.begin(); it != AET.end(); ++it) {
	if (it->y_upper > y) {
		newAET.push_back(*it);
	}
}
AET = newAET;

//检查是否有新的边加入
if (it_ET != ET.end() && y >= it_ET->first) {
	AET.insert(AET.begin(), it_ET->second.begin(), it_ET->second.end());
	it_ET++;
}

获取当前扫描线的所有交点

auto it = AET.begin();
while (it != AET.end())
{
	float x1 = it->x_lower;
	it->x_lower += it->dx;
	it++;

	if (it != AET.end())
	{
		float x2 = it->x_lower;
		it->x_lower += it->dx;
		it++;

		// 扫描线遇到两条线相交的顶点时，不记录交点
		if (x1 != x2)
		{
			scanPoints.push_back(CPoint(x1, y));
			scanPoints.push_back(CPoint(x2, y));
		}
	}
}

交点排序并填充

// 比较函数，按照CPoint对象的x值升序排列
bool CPolygonFillDlg::compareCPoint(const CPoint& a, const CPoint& b) {
	return a.x < b.x;
}

// 对扫描到的所有交点进行升序排列
std::sort(scanPoints.begin(), scanPoints.end(), compareCPoint);

// 获取画板
CStatic* CANVAS = (CStatic*)GetDlgItem(IDC_STATIC_CANVAS);
CDC* pDC = CANVAS->GetDC();
// 成对绘制，i每次+2
for (int i = 0; i < scanPoints.size(); i += 2)
{
	pDC->MoveTo(scanPoints[i]);
	pDC->LineTo(scanPoints[i + 1]);
}
ReleaseDC(pDC);

实验结果

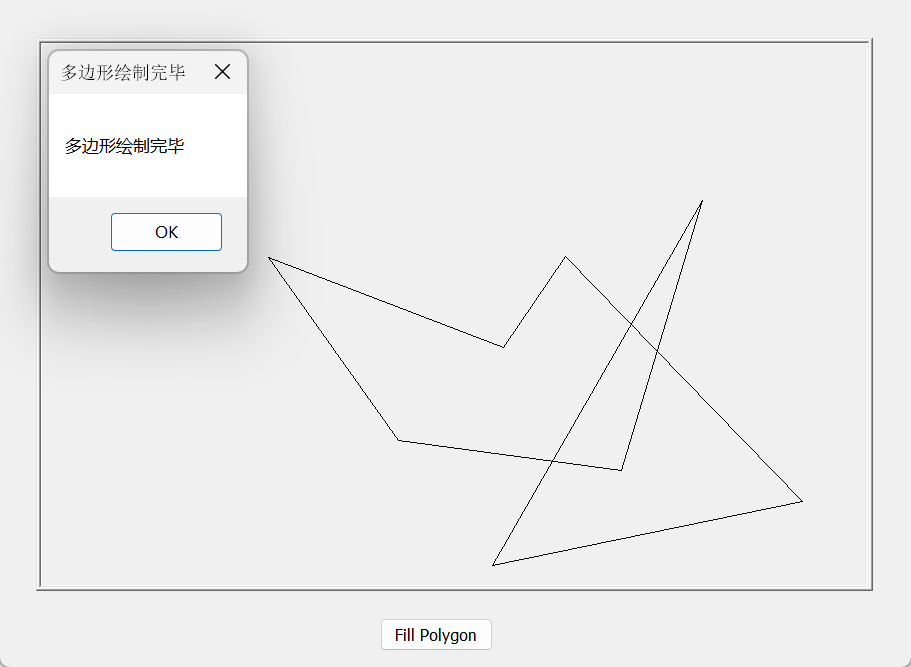
image-20231025213116930

如上图，通过左键点击绘制多边形，右键点击结束绘制

绘制成功后会弹出绘制完毕的提示框

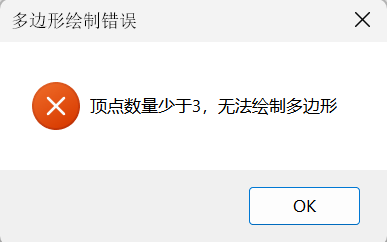
如果多边形顶点少于3个，则弹出错误提示框如下：

image-20231025213258682

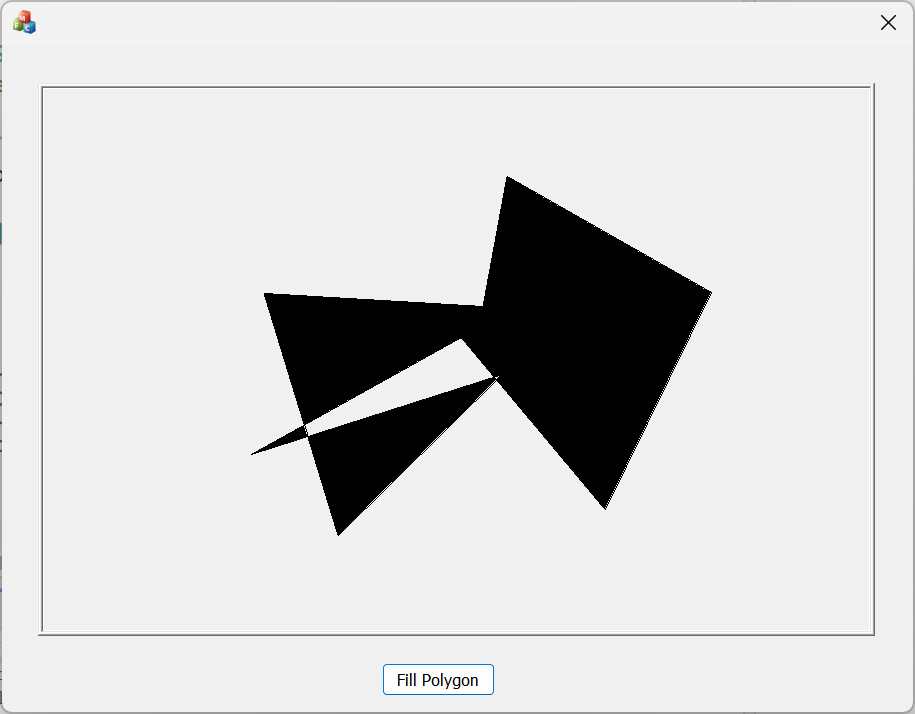
随后点击Fill Polygon按钮，运行扫描线填充，结果如下：

  • 凸多边形
    ​ image-20231025213412123
  • 凹多边形
    ​ image-20231025213526340
  • 边相交
    ​ image-20231025213430842
# mfc # c++
Logo
开放原子开发者工作坊

开放原子开发者工作坊旨在鼓励更多人参与开源活动，与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动，如meetup、训练营等，主打技术交流，干货满满，真诚地邀请各位开发者共同参与！

更多推荐

第二届开放原子大赛首批创新成果集结武汉，诚邀广大开发者共鉴开源技术盛宴

第二届开放原子大赛首批创新成果集结武汉，诚邀广大开发者共鉴开源技术盛宴

avatar 开放原子开发者工作坊

诚邀报名 | 开源基础设施能力建设分论坛：打造开源生态的“心脏”

诚邀报名 | 开源基础设施能力建设分论坛：打造开源生态的“心脏”

avatar 开放原子开发者工作坊

诚邀报名 | 编程语言分论坛：AI时代的技术革新与开源实践

诚邀报名 | 编程语言分论坛：AI时代的技术革新与开源实践

avatar 开放原子开发者工作坊